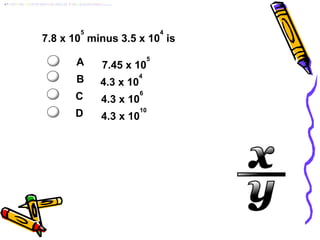The document provides instructions on how to add and subtract numbers in scientific notation, emphasizing that exponents must be the same for operations to be performed. It outlines specific steps for both addition and subtraction when exponents are the same or different, including rewriting numbers to match exponents. Several examples and practice problems illustrate these rules for clarity.

1. Adding and Subtracting
Adding and Subtracting
Numbers in Scientific Notation
Numbers in Scientific Notation

2. Using Scientific
Notation in
Multiplication,
Division,
Addition and
Subtraction
Scientists must be
able to use very
large and very small
numbers in
mathematical
calculations. As a
student in this class,
you will have to be
able to multiply,
divide, add and
subtract numbers
that are written in
scientific notation.
Here are the rules.

3. When adding or
subtracting numbers in
scientific notation, the
exponents must be the
same.

4. Adding/Subtracting when
Exponents are THE SAME
Step 1 - add/subtract the decimal
Step 2 – Bring down the given exponent
on the 10

5. Example 1
(2.56 X 103
) + (6.964 X 103
)
Step 1 - Add:
2.56 + 6.964 =
9.524
Step 2 – Bring down exponent :
9.524 x 103

6. Example 2
(9.49 X 105
) – (4.863 X 105
)
Step 1 - Subtract:
9.49 – 4.863 =
4.627
Step 2 – Bring down exponent:
4.627 x 105

7. The sum of 5.6 x 10
3
and 2.4 x 10
3
is
A 8.0 x 10
3
B 8.0 x 10
6
C 8.0 x 10
-3
D 8.53 x 10
3

8. The sum of 5.6 x 10
3
and 2.4 x 10
3
is
A 8.0 x 10
3
B 8.0 x 10
6
C 8.0 x 10
-3
D 8.53 x 10
3
The exponents are the
same, so add the
coefficients.

9. 8.0 x 10
3
minus 2.0 x 10
3
is
A 6.0 x 10
-3
B 6.0 x 10
0
C 6.0 x 10
3
D 7.8 x 10
3

10. 8.0 x 10
3
minus 2.0 x 10
3
is
A 6.0 x 10
-3
B 6.0 x 10
0
C 6.0 x 10
3
D 7.8 x 10
3

11. Adding/Subtracting when the
Exponents are DIFFERENT
• When adding or subtracting numbers
in scientific notation, the exponents
must be the same.
• If they are different, you must move
the decimal so that they will have the
same exponent.

12. Moving the Decimal
It does not matter which number you
decide to move the decimal on, but
remember that in the end both
numbers have to have the same
exponent on the 10.

13. Adding/Subtracting when the
Exponents are DIFFERENT
Step 1 – Rewrite so the exponents are the
same
Step 2 - add/subtract the decimal
Step 3 – Bring down the given exponent on
the 10

14. Adding With Different
Exponents
• (4.12 x 106
) + (3.94 x 104
)
• (412 x 104
) + (3.94 x 104
)
• 412 + 3.94 = 415.94
• 415.94 x 104
• Express in proper form: 4.15 x 106

15. Subtracting With Different
Exponents
• (4.23 x 103
) – (9.56 x 102
)
• (42.3 x 102
) – (9.56 x 102
)
• 42.3 – 9.56 = 32.74
• 32.74 x 102
• Express in proper form: 3.27 x 103

16. Example 3
(2.46 X 106
) + (3.4 X 103
)
Step 1 – Rewrite with the same exponents
3.4 X 103

0.0034 X 103+3
New Problem: (2.46 X 106
) + (0.0034 X 106
)
Step 2 – Add decimals
2.46 + 0.0034 =
2.4634
Step 3 – Bring Down Exponents
2.4634 X 106

17. Example 4
(5.762 X 103
) – (2.65 X 10-1
)
Step 1 – Rewrite with the same exponents
2.65 X 10-1

0.000265 X 10(-1+4)
New Problem : (5.762 X 103
) – (0.000265 X 103
)
Step 2 – Subtract Decimals
5.762 – 0.000265 =
5.762
Step 3 – Bring down decimals
5.762 X 103

18. 7.0 x 10
3
plus 2.0 x 10
2
is
A 9.0 x 10
3
B 9.0 x 10
5
C 7.2 x 10
3
D 7.2 x 10
2

19. 7.0 x 10
3
plus 2.0 x 10
2
is
A 9.0 x 10
3
B 9.0 x 10
5
C 7.2 x 10
3
D 7.2 x 10
2

20. 7.8 x 10
5
minus 3.5 x 10
4
is
A 7.45 x 10
5
B 4.3 x 10
4
C 4.3 x 10
6
D 4.3 x 10
10

21. 7.8 x 10
5
minus 3.5 x 10
5
is
A
B 4.3 x 10
4
C 4.3 x 10
6
D 4.3 x 10
10
7.45 x 10
5

22. Adding and Subtracting…
• The important thing to remember about
adding or subtracting is that the
exponents must be the same!
– If the exponents are not the same then it is
necessary to change one of the numbers
so that both numbers have the same
exponential value.

23. Practice
1) (3.45 x 103
) + (6.11 x 103
)
2) (4.12 x 106
) + (3.94 x 104
)
1) (8.96 x 107
) – (3.41 x 107
)
2) (4.23 x 103
) – (9.56 x 102
)