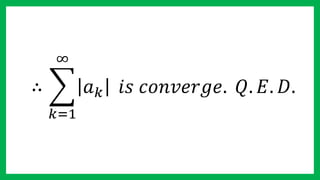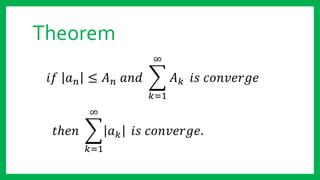
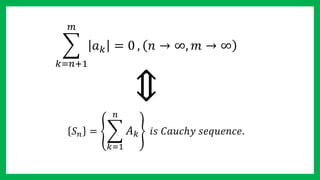
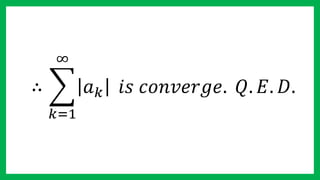
This document presents a direct comparison test theorem for determining if a series converges or diverges. It states that if the sequence of partial sums of another series AN is convergent, and the terms of the series an are less than or equal to the corresponding terms of AN for all n, then the series of an must also converge. It then provides a proof of this theorem showing that if the sequence of partial sums of AN approaches 0 as n and m approach infinity, then the sequence of partial sums of an must also approach 0, and therefore an converges.

1. DIRECT COMPARISON TEST
Hanpen Robot
Sunday January 17 2016

2. 𝑖𝑓 𝑎 𝑛 ≤ 𝐴 𝑛 𝑎𝑛𝑑
𝑘=1
∞
𝐴 𝑘 𝑖𝑠 𝑐𝑜𝑛𝑣𝑒𝑟𝑔𝑒
𝑡ℎ𝑒𝑛
𝑘=1
∞
𝑎 𝑘 𝑖𝑠 𝑐𝑜𝑛𝑣𝑒𝑟𝑔𝑒.
Theorem

3. 0 ≤
𝑘=𝑛+1
𝑚
𝑎 𝑘 ≤
𝑘=𝑛+1
𝑚
𝐴 𝑘 = 0, (𝑛 → ∞, 𝑚 → ∞)
Proof:
∴
𝑘=𝑛+1
𝑚
𝑎 𝑘 = 0 , (𝑛 → ∞, 𝑚 → ∞)

4. 𝑘=𝑛+1
𝑚
𝑎 𝑘 = 0 , 𝑛 → ∞, 𝑚 → ∞
⇕
𝑆 𝑛 =
𝑘=1
𝑛
𝐴 𝑘 𝑖𝑠 𝐶𝑎𝑢𝑐ℎ𝑦 𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒.

5. ∴
𝑘=1
∞
𝑎 𝑘 𝑖𝑠 𝑐𝑜𝑛𝑣𝑒𝑟𝑔𝑒. 𝑄. 𝐸. 𝐷.

6. THE END