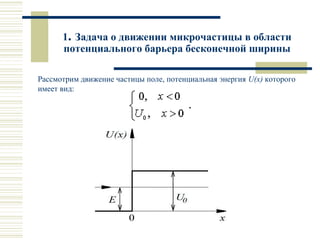
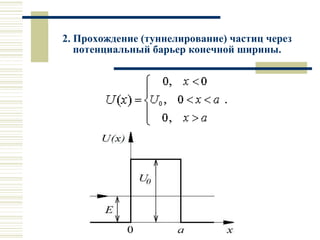
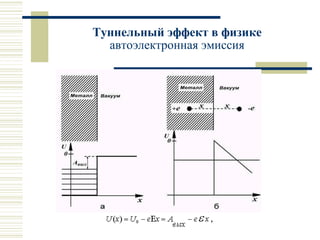
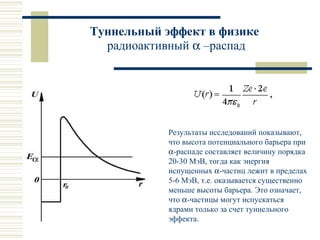
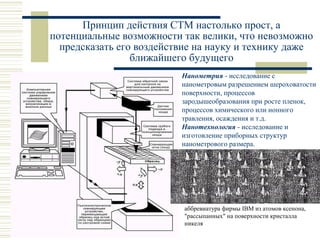
Лекция посвящена движению частиц в области потенциального барьера и туннельному эффекту. Рассматриваются математические модели для микрочастиц при высоких и низких потенциальных барьерах, а также применения туннельного эффекта в автоэлектронной эмиссией, радиоактивном альфа-распаде и работе сканирующего туннельного микроскопа. Обсуждаются технические детали и важность применения туннельного эффекта в нанотехнологиях.

1. Лекция №6.
Движение частицы в области потенциального
барьера. Туннельный эффект.
План:
1. Задача о движении микрочастицы в области
потенциального барьера бесконечной
ширины.
2. Прохождение (туннелирование) частиц через
потенциальный барьер конечной ширины.
3. Туннельный эффект и его применение.

2. 1. Задача о движении микрочастицы в области
потенциального барьера бесконечной ширины
Рассмотрим движение частицы поле, потенциальная энергия U(x) которого
имеет вид:

3. Решение уравнения Шредингера
Область слева от барьера обозначим I и соответствующие решения индексом 1,
а справа от порога II и индексом 2.
Уравнение Шредингера для области I имеет вид:
а для области II:
Рассмотрим сначала случай, когда энергия E частицы меньше высоты
потенциального барьера Uo , т.е. E<Uo. Говорят, что в этом случае мы имеем
дело с высоким потенциальным барьером. Введем обозначения:
(1)

4. Решение уравнения Шредингера
Получаем следующие уравнения Шредингера для областей I и II:
(2)
(3)
Решения этих уравнений имеют следующий вид:
(4)
(5)
Первое слагаемое в волновых функциях представляет собой плоскую волну де
Бройля, распространяющуюся вдоль оси слева направо. Аналогично, второе
слагаемое в описывает плоскую дебройлевскую волну, распространяющуюся
вдоль оси в отрицательном направлении справа налево.

5. Применение граничных условий
Волновая функция на границе раздела областей I и II должна быть не только
непрерывной, но и гладкой, т.е. иметь непрерывную производную.
Приравнивание волновых функций и их производных на границе раздела двух
областей, в которых волновая функция имеет разный вид, получило название
сшивки волновых функций и их производных. В данном случае условия
сшивки имеют вид:
что приводит к:
Положим , а равным нулю, т.к. нет условий для отражения в
области II.

6. Анализ решения
Остальные коэффициенты имеют следующий вид:
Тогда волновые функции можно записать в следующем виде:
Найдем коэффициент отражения, определяющий вероятность того, что частица
отразится от высокого порога. Согласно физическому смыслу, коэффициент
отражения R есть
2
1
2
1
A
B
R =

7. Коэффициенты отражения и
прохождения
После подстановки получим:
Коэффициент прохождения D частицы через барьер определяется из условия:
То есть:
Плотность вероятности нахождения частицы в области II:
Т.е. при малых x вероятность обнаружить частицу в области II отлична от нуля:
Так при x=0.1 нм и U0 -E=1 эВ: Но уже при x= 1 нм и U0-E=1 эВ:
1=+ DR

8. Низкий потенциальный барьер
Теперь рассмотрим случай, когда энергия E частицы больше высоты
потенциального барьера Uo , т.е. E>Uo. Говорят, что в этом случае мы имеем
дело с низким потенциальным барьером.
Соответствующие решения уравнений Шредингера можно записать в
следующем виде:
Т.к. коэффициент B1 отличен от нуля, то возможно «надбарьерное отражение»
R =

9. 2. Прохождение (туннелирование) частиц через
потенциальный барьер конечной ширины.

10. Уравнения Шредингера
Уравнения Шредингера для каждой из областей имеют следующий вид:
Решение каждого из них:

11. Туннелирование частиц через барьер
Применение граничных условий к волновым функциям позволяет получить
следующее выражение для коэффициента прохождения:
Прохождение частицы через потенциальный барьер, высота которого
превышает энергию частицы, получило название туннельного эффекта
(частица, проходя под барьером, как бы движется в туннеле). Отметим, что
туннельный эффект представляет собой чисто квантовое явление. Квантовая
частица может пройти через высокий потенциальный барьер, причем
вероятность ее прохождения испытывает сильную (экспоненциальную)
зависимость от массы частицы, а также от вида потенциального барьера U(x) .
Подчеркнем, что при прохождении через барьер полная энергия частицы Е
не меняется !!!.

12. Туннельный эффект в физике
автоэлектронная эмиссия

13. Туннельный эффект в физике
радиоактивный α –распад
Результаты исследований показывают,
что высота потенциального барьера при
α-распаде составляет величину порядка
20-30 МэВ, тогда как энергия
испущенных α-частиц лежит в пределах
5-6 МэВ, т.е. оказывается существенно
меньше высоты барьера. Это означает,
что α-частицы могут испускаться
ядрами только за счет туннельного
эффекта.

14. Сканирующий туннельный микроскоп
Сканирующий туннельный микроскоп
(СТМ) был создан в 1982 г сотрудниками
исследовательского отдела фирмы IBM Г.
Биннигом и Х. Рёрером. Он открыл очень
многообещающие возможности научных
и прикладных исследований в области
нанотехники. За создание СТМ Г. Бинниг
и Х. Рёрер в 1986 году были удостоены
Нобелевской премии по физике.
Принцип работы СТМ заключается в следующем: к поверхности проводящего
образца на характерное межатомное расстояние, составляющее доли нанометра,
подводится очень тонкое металлическое острие (игла). При приложении между
образцом и иглой разности потенциалов ~ 0,11 В в цепи (см. рис.) появляется
ток, обусловленный туннелированием электронов через зазор между ними.

15. Сканирующий туннельный микроскоп
Существуют два варианта режима работы
СТМ : режим постоянной высоты и режим
постоянного тока. При работе в режиме
постоянной высоты острие иглы перемещается
в горизонтальной плоскости над исследуемой
поверхностью (рис. а ). Туннельный ток при
этом изменяется и по этим изменениям легко
может быть определен рельеф поверхности
образца. При работе в режиме постоянного тока
(рис. б) используется система обратной связи,
которая поддерживает постоянным туннельный
ток за счет перемещения острия иглы в
вертикальном направлении. В этом случае
информация о рельефе поверхности получается
на основании данных о перемещении иглы.

16. Принцип действия СТМ настолько прост, а
потенциальные возможности так велики, что невозможно
предсказать его воздействие на науку и технику даже
ближайшего будущего
Нанометрия - исследование с
нанометровым разрешением шероховатости
поверхности, процессов
зародышеобразования при росте пленок,
процессов химического или ионного
травления, осаждения и т.д.
Нанотехнология - исследование и
изготовление приборных структур
нанометрового размера.
аббревиатура фирмы IBM из атомов ксенона,
"рассыпанных" на поверхности кристалла
никеля

17. Лекция окончена
Спасибо за внимание