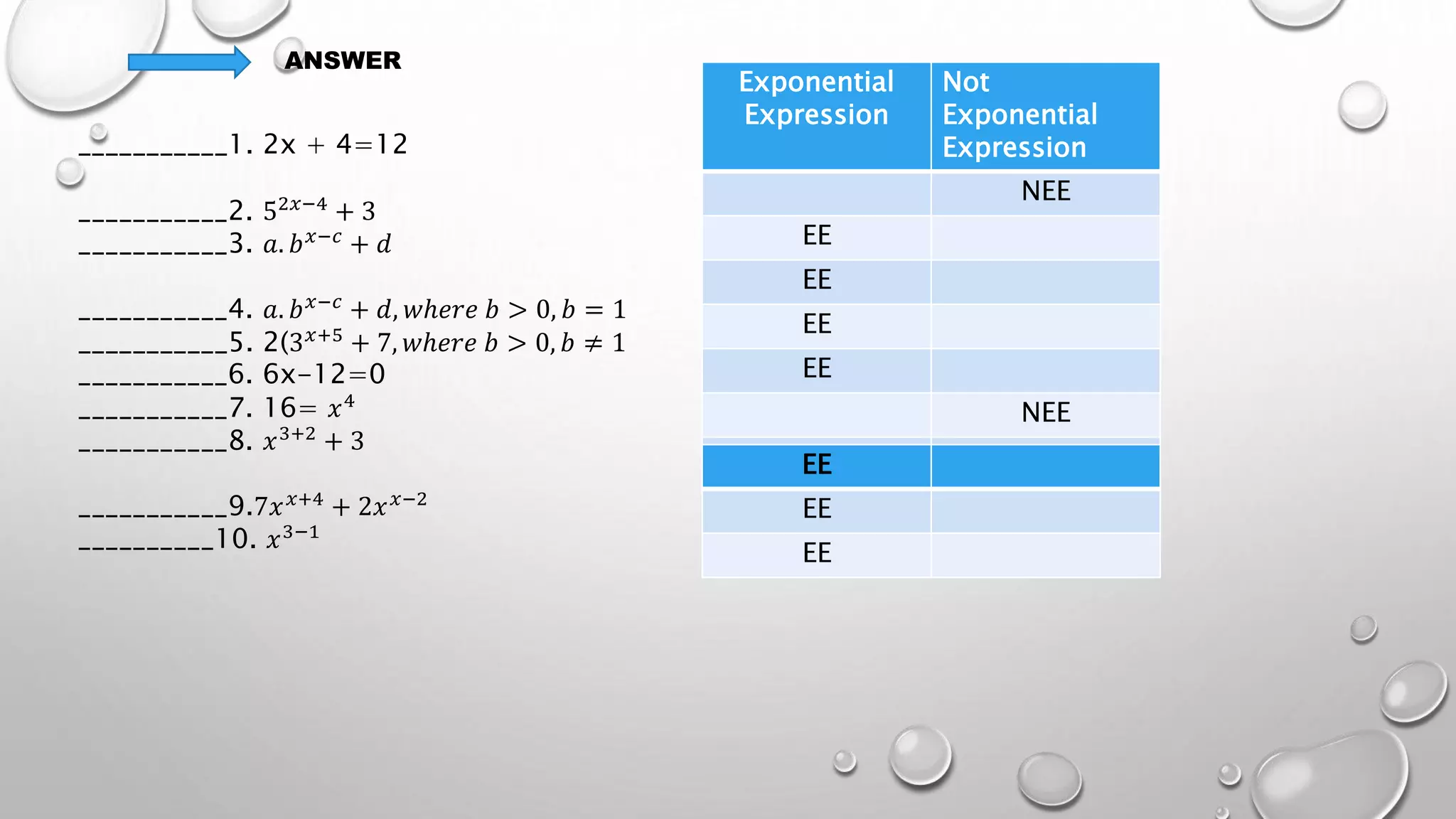
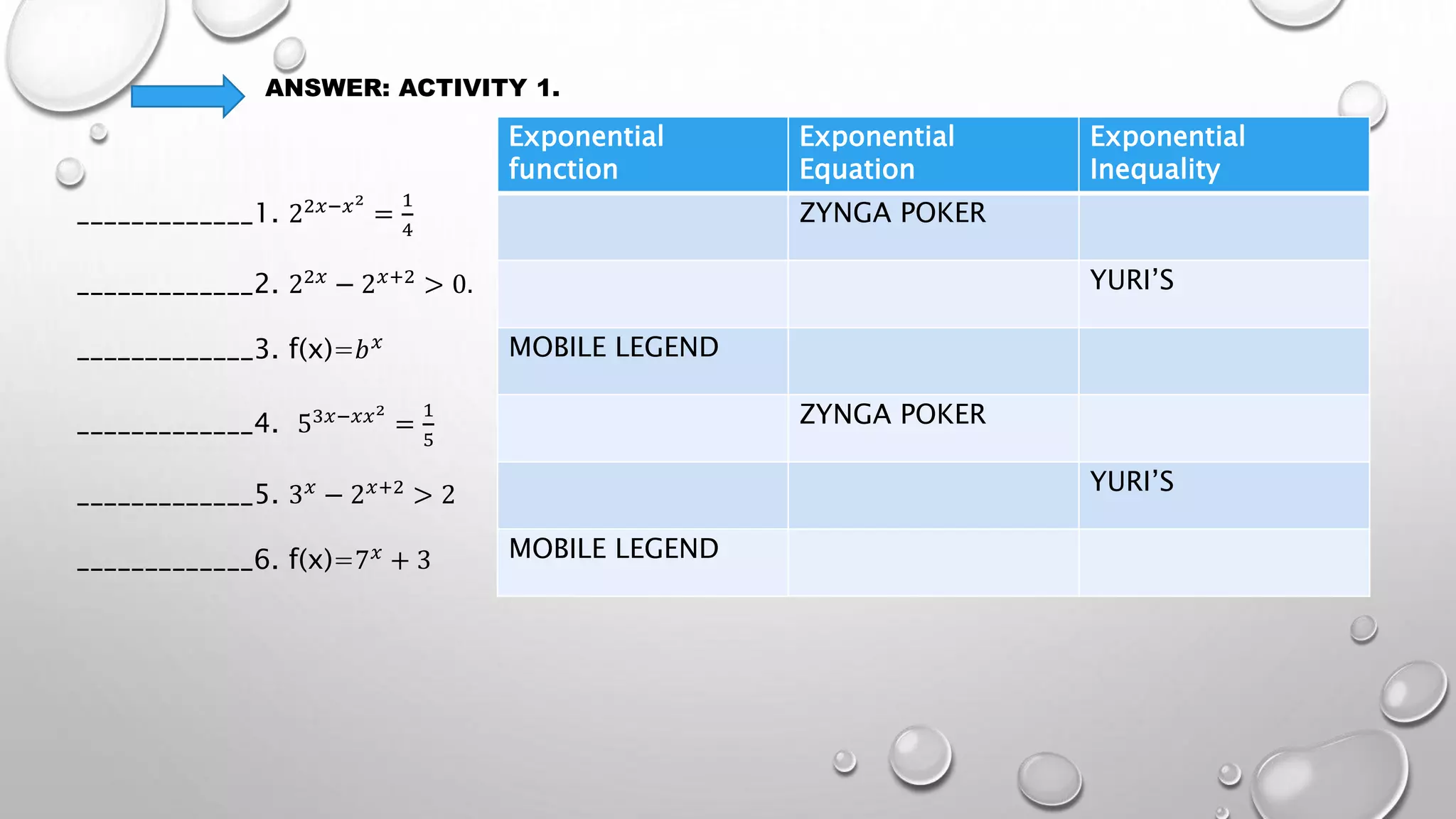
The document discusses distinguishing between exponential functions, equations, and inequalities. It aims to teach the differences between exponential expressions, functions, equations, and inequalities. Several examples are provided to identify which category expressions fall into. Learners are assessed through multiple choice and true/false questions to evaluate their understanding of the key differences between exponential functions, equations, and inequalities.

1. DISTINGUISHES BETWEEN
EXPONENTIAL FUNCTION,
EQUATIONS AND
INEQUALITY
DETERMINING THE DIFFERENCES OF EXPONENTIAL
FUNCTIONS, EQUATIONS AND INEQUALITIES

2. • OBJECTIVES:M11GM-IE-4
AT THE END OF THE LESSON, YOU SHOULD BE ABLE TO:
1. DISTINGUISHES THE DIFFERENCE BETWEEN
EXPONENTIAL, FUNCTION, EXPONENTIAL EQUATION, AND
EXPONENTIAL INEQUALITY.
2. EXPLAIN THE MATHEMATICAL DIFFERENCE OF
EXPONENTIAL FUNCTION, EQUATIONS AND INEQUALITY IN
ITS SIMPLEST FORM.
3. APPRECIATE THE DIFFERENCES OF EXPONENTIAL
FUNCTION, EXPONENTIAL EQUATION AND EXPONENTIAL

3. A. REVIEWING PREVIOUS LESSON OR
PRESENTING THE NEW LESSON

4. B. ESTABLISHING A PURPOSE
FOR THE LESSON
IDENTIFY THE FOLLOWING IF IT IS AN EXPONENTIAL EXPRESSION OR NOT. WRITE EE IF IT IS AN
EXPONENTIAL EXPRESSION AND NEE IF IT IS NOT EXPONENTIAL EXPRESSION IN THE BOX
PROVIDED.
___________1. 2X + 4=12
___________2. 52𝑥−4
+ 3
___________3. 𝑎. 𝑏𝑥−𝑐
+ 𝑑
___________4. 𝑎. 𝑏𝑥−𝑐
+ 𝑑, 𝑤ℎ𝑒𝑟𝑒 𝑏 > 0, 𝑏 = 1
___________5. 2(3𝑥+5
+ 7, 𝑤ℎ𝑒𝑟𝑒 𝑏 > 0, 𝑏 ≠ 1
___________6. 6X-12=0
___________7. 16= 𝑥4
___________8. 𝑥3+2
+ 3
___________9.7𝑥𝑥+4
+ 2𝑥𝑥−2
__________10. 𝑥3−1
Exponential
Expression
Not
Exponential
Expression

5. ANSWER
___________1. 2x + 4=12
___________2. 52𝑥−4
+ 3
___________3. 𝑎. 𝑏𝑥−𝑐
+ 𝑑
___________4. 𝑎. 𝑏𝑥−𝑐 + 𝑑, 𝑤ℎ𝑒𝑟𝑒 𝑏 > 0, 𝑏 = 1
___________5. 2(3𝑥+5 + 7, 𝑤ℎ𝑒𝑟𝑒 𝑏 > 0, 𝑏 ≠ 1
___________6. 6x-12=0
___________7. 16= 𝑥4
___________8. 𝑥3+2 + 3
___________9.7𝑥𝑥+4
+ 2𝑥𝑥−2
__________10. 𝑥3−1
Exponential
Expression
Not
Exponential
Expression
NEE
EE
EE
EE
EE
NEE
EE
EE
EE
EE

6. C. PRESENTING EXAMPLES / INSTANCES OF THE NEW
LESSON
ACTIVITY 1.
DIRECTION: IDENTIFY THE FOLLOWING EXPRESSION, WRITE MOBILE LEGEND IF THE
EXPRESSION IS EXPONENTIAL FUNCTION, ZYNGA POKER FOR EXPONENTIAL EQUATION AND
YURI’S IF THE EXPRESSION IS AN EXAMPLE OF EXPONENTIAL INEQUALITY. WRITE YOUR
ANSWER IN YOUR ACTIVITY NOTEBOOK.
_____________1. 22𝑥−𝑥2
=
1
4
_____________2. 22𝑥
− 2𝑥+2
> 0.
_____________3. F(X)=𝑏𝑥
_____________4. 53𝑥−𝑥𝑥2
=
1
5
_____________5. 3𝑥 − 2𝑥+2 > 2
_____________6. F(X)=7𝑥
+ 3
Exponential
function
Exponential
Equation
Exponential
Inequality

7. ANSWER: ACTIVITY 1.
_____________1. 22𝑥−𝑥2
=
1
4
_____________2. 22𝑥 − 2𝑥+2 > 0.
_____________3. f(x)=𝑏𝑥
_____________4. 53𝑥−𝑥𝑥2
=
1
5
_____________5. 3𝑥 − 2𝑥+2 > 2
_____________6. f(x)=7𝑥
+ 3
Exponential
function
Exponential
Equation
Exponential
Inequality
ZYNGA POKER
YURI’S
MOBILE LEGEND
ZYNGA POKER
YURI’S
MOBILE LEGEND

8. D. DISCUSSING NEW CONCEPTS AND
PRACTICING NEW SKILLS #1
TRY THIS ONE, ENJOY !ACTIVITY 2
DIRECTION: GROUP YOUR SELF INTO 3 MEMBERS PER TEAM, THEN, GIVE THE
FOLLOWING.
1. GIVE AN EXAMPLE OF AN EXPONENTIAL FUNCTION THROUGH A MOBILE LEGEND
CHARACTERS.
___________________
2. GIVE AN EXAMPLE OF AN EXPONENTIAL EQUATION USING YOUR MOBILE LEGEND
FAVORATE
CHARACTER’S POWER ITEMS.
___________________
3. GIVE AN EXAMPLE OF AN EXPONENTIAL INEQUALITY BY YOUR FAVORATE ANIME
CHARACTERS.
___________________

9. GROUP 1 OUTPUT- EXPONENTIAL FUNCTION
Exponential function using mobile legend line ups:
1. Tank- Tigreal is a tank who had a crowd control of a team clash, it can stun and freeze the
enemy lifting it up in the air.
2. Assassin-Zlong is an assassin type of hero who can use its full attack on heroes that will be
stun by friendlies and can execute a quick demise of the hero opponent.
3. Marksman- Yi Shun Shin is a marksman assassin who can act as a long hand support hero, at
the same time can deals damage in hand to hand combat and assassination.
4. Mage-Kadita is a mage assassin tank type of hero that can control the crowd during clash battle,
it can also petrify enemy with small life line.
5. Support-Estes is a support hero who have a very unique traits and power source distributor
especially during team clashes, restoring his team mates life line.
Therefore with this Line ups of Heroes, the exponential powers combined by this character can surely
give an advantage and winability of the team using it. The lethal combinations will give and escalate a
massive Exponential growth in all aspect of the game.

10. GROUP 2 OUTPUT-
EXPONENTIAL EQUATION
LAYLA MARKSMAN MIYA
4 DURABILITY 5
9 OFFENSE 10
8 SKILL EFFECTS 7
5 DIFFICULTY 4
REAP/DAMAGE SPECIALTY REAP/ DAMAGE
Therefore, the two marksman heroes have an equal capability in terms if there Skills and ability, with
emblems and battle equipment's, both heroes can increase its skills and ability exponentially.

11. GROUP 3 OUTPUT-EXPONENTIAL INEQUALITIES
*Guko and Naruto are both manga and anime character, two super anime
character that is been loved by fans because of their tenacity and power level,
the progress of their powers, skills, ability and tenacity evolves in the highest
form a manga or anime character can achieve.
*Eventually, in terms of all the aspect being said and given, we could say that
GUKO UMNI-GOD FORM has too far powerful exponentially than of NARUTO
HOKAGE FORM with the scale of 100 million to 10 million ratio.

12. E. DISCUSSING NEW CONCEPTS AND PRACTICING SKILLS #2
• BRAINSTORMING
* OPEN DISCUSSION ABOUT THE TOPIC
* FEEDBACKS AND CLARIFICATIONS
* PERSONAL POINT OF VIEWS
* OTHERS

13. F. DEVELOPING MASTERY (LEADS TO FORMATIVE ASSESSMENT)
ACTIVITY 3. DIRECTION: MATCH THE EXPRESSION IN COLUMN A TO COLUMN B, SELECT YOUR ANSWER INSIDE THE BOX, THEN WRITE
YOUR ANSWER IN YOUR ACTIVITY NOTEBOOK.
COLUMN A COLUMN B
_____1. F(X)=𝑐𝑥
EXPONENTIAL EQUATION
_____2. 3𝑥−2
+ 1 > 0 EXPONENTIAL FUNCTION
_____3. 3𝑥+1
= 9 EXPONENTIAL INEQUALITY
_____4. 64= 2𝑥3
_____5.
1
3
(2𝑥
) ≥
2
3
_____6. G (X) = 3𝑥2+2
+ 5

14. ANSWER: ACTIVITY 3
1.Exponential Function
2.Exponential Inequality
3.Exponential Equation
4.Exponential Equation
5.Exponential Inequality
6.Exponential Function
Checked your Answers: Did you answer
it this way?

15. G. FINDING PRACTICAL APPLICATIONS OF CONCEPTS AND SKILLS IN DAILY LIVING
FOR YOUR INFORMATION
APPLICATION OF EXPONENTIAL FUNCTION, EQUATION AND INEQUALITY TO REAL-LIFE.
* BACTERIAL GROWTH/ DECAY
* POPULATION GROWTH/DECLINE
* COMPOUND INTEREST

16. H. MAKING GENERALIZATIONS AND ABSTRACTIONS ABOUT THE LESSON
DIFFERENCES BETWEEN EXPONENTIAL INEQUALITY, EXPONENTIAL EQUATION AND EXPONENTIAL FUNCTION.
LET US DIFFERENTIATE THE DIFFERENCES OF THIS THREE EXPRESSION BY DETERMINING ITS TREATS AND WHAT ARE THEIR USES.
EXPONENTIAL INEQUALITY
*EXPONENTIAL INEQUALITY DEFINES AS INEQUALITIES WHICH HAVE VARIABLES IN THE EXPONENTS. (NOTE: THE BASIC PROPERTIES OF
EXPONENT, LOOK AT THE EXPRESSION BELOW.)
𝑎𝑏
WHEN YOU SAID INEQUALITY, MEANING YOUR USING THE VERY BASIC SYMBOLS OF INEQUALITIES SUCH AS FOLLOWS. ≠, <, >, ≤, ≥
EXAMPLES OF EXPONENTIAL INEQUALITY
EXAMPLE1 EXAMPLE2 EXAMPLE3 EXAMPLE4
43𝑥+2
< 64 2𝑥+1
≥ 42𝑥−1
52𝑥
− 5𝑥+1
> 0 3𝑥+2
≠ 3𝑥−2
EXAMPLE 5
42𝑥+1
≤ 2𝑥+1
a is the
base
b is the
exponent

17. EXPONENTIAL EQUATION
• An Exponential Equation is one which a variable occurs in the exponent, for
example, when both side of the equation have the same base, the
exponents on either side are equal by the property.
Examples of an Exponential Equations
Example1 Example2
72𝑥+1
= 16807 24𝑥
=23𝑥+1
Example3 Example4
3𝑥+3 = 243 2𝑥
1
2
= 2

18. EXPONENTIAL FUNCTION
* AN EXPONENTIAL FUNCTION IS A MATHEMATICAL FUNCTION OF THE FOLLOWING
FORM: F(X) =𝑎𝑥
. WHERE X IS A VARIABLE AND A IS A CONSTANT CALLED THE BASE OF
THE FUNCTION. THE MOST COMMONLY ENCOUNTERED EXPONENTIAL FUNCTION BASE IS
TRANSCENDENTAL NUMBER E, WHICH IS EQUAL TO APPROXIMATELY 2.71828
.F(X)=𝑏𝑥
EXAMPLE1
F(X) = 𝑏𝑥
, 𝑏 > 0, 𝑏 ≠ 1
EXAMPLE2
G(X) = 8𝑥
+3
EXAMPLE3
H(X)= 2𝑥+1+3

19. DIFFERENCES BETWEEN EXPONENTIAL INEQUALITY, EXPONENTIAL
EQUATION AND EXPONENTIAL FUNCTION
• NOW LET US SUMMED UP THE DIFFERENCES OF THE THREE EXPRESSION.
• FIRST, EXPONENTIAL EQUATION USUALLY USE AND REPRESENTS WITH AN EQUAL SIGNS. ( = )
AND THAT OF INVOLVES PROBLEMS WITH EXPONENTIAL EXPRESSION.
• SECOND, EXPONENTIAL INEQUALITY USUALLY USE OR REPRESENTS BY INEQUALITY SYMBOL
SUCH AS (<, >, ≤, ≥, ≠) AND THAT OF INVOLVES PROBLEMS WITH EXPONENTIAL EXPRESSION.
• THIRD, EXPONENTIAL FUNCTION IS IN THE FORM OF F(X)=𝑏𝑥
WHERE B> 0 𝑎𝑛𝑑 𝑡ℎ𝑎𝑡 𝑏 𝑖𝑠 𝑛𝑜𝑡 ≠
1 AND THAT EXPONENT X IS IN RELATION WITH THE F(X) OR Y.
• MOREOVER THE FIRST TWO EXPRESSION THE EXPONENTIAL EQUATION AND EXPONENTIAL
INEQUALITY, YOU CAN SOLVE FOR THE VALUE OF X, WHILE EXPONENTIAL FUNCTION IS THE
RELATION BETWEEN THE X AS AN EXPONENT AND THE F(X) OR Y.

20. COMPARISON
Exponential
Equation
( = )
Exponential
Inequality
(<, >, ≤, ≥, ≠)
Exponential
function
f (x), g(x),h (x)
72𝑥−𝑥2
= 7 5𝑥+1
− 5𝑥
> 0 f (x)= 7𝑥
+ 3

21. I. EVALUATING LEARNING
ASSESSMENT
A. DIRECTION: MULTIPLE CHOICE, SELECT THE BEST ANSWER IN EVERY QUESTION. WRITE YOUR ANSWER IN
YOUR ACTIVITY NOTEBOOK.
_______1. AN ________________IS A MATHEMATICAL FUNCTION OF THE FOLLOWING FORM: F(X) =𝑎𝑥
. WHERE X IS A VARIABLE
AND A IS A CONSTANT CALLED THE BASE OF THE FUNCTION.
A. EXPONENTIAL FUNCTION B. EXPONENTIAL INEQUALITY C. EXPONENTIAL EQUATION D.
EXPONENTIAL EXPRESSION
_______2. AN __________________IS ONE WHICH A VARIABLE OCCURS IN THE EXPONENT, FOR EXAMPLE, WHEN BOTH SIDE OF
THE EQUATION HAVE THE SAME BASE, THE EXPONENTS ON EITHER SIDE ARE EQUAL BY THE PROPERTY.
A. EXPONENTIAL FUNCTION B. EXPONENTIAL INEQUALITY C. EXPONENTIAL EQUATION D.
EXPONENTIAL EXPRESSION
_______3. AN __________________DEFINES AS INEQUALITIES WHICH HAVE VARIABLES IN THE EXPONENTS.
A. EXPONENTIAL FUNCTION B. EXPONENTIAL INEQUALITY C. EXPONENTIAL EQUATION D.
EXPONENTIAL EXPRESSION
_______4. EXPONENTIAL FUNCTION USUALLY REPRESENTS BY_____________ AS A SIGN AND SYMBOL.
A. F(X)=𝑏𝑥
, B> 0 , 𝑏 ≠ 1 B. . F(X)=𝑏𝑥
, B> 0 , 𝑏 = 1 C. . F(X)=𝑏𝑥
, B> 0 , 𝑏 ≥ 1 D. . F(X)=𝑏𝑥
, B> 0 , 𝑏 ≤ 1
_______5. WHEN YOU SAID INEQUALITY, MEANING YOUR USING THE VERY BASIC SYMBOLS OF INEQUALITIES ARE
______________________.

22. B. DIRECTION: WRITE TRUE IF THE STATEMENT IS CORRECT AND FALSE IF IT
IS WRONG.
______6. THE SYMBOL REPRESENT F(X) REPRESENTS INEQUALITY?
______7. SYMBOLS SUCH AS . (≠, <, >, ≤, ≥) REPRESENTS EQUATION?
______8. EXPONENTIAL INEQUALITY USUALLY USE TO SOLVE PROBLEMS THAT INVOLVES
INEQUALITY EXPRESSION?
______9. THE SYMBOL G(X) OR H (X) ALSO USE TO SOLVE OR REPRESENT EXPONENTIAL
FUNCTION?
_____10. MOST EQUATION WITH THE SAME BASE AND X AS AN EXPONENTIAL PROBLEM
COMMONLY REPRESENTS EXPONENTIAL EQUATION?

23. ANSWER
ASSESSMENT
A.
1.A (EXPONENTIAL FUNCTION)
2.C (EXPONENTIAL EQUATION)
3.B (EXPONENTIAL INEQUALITY)
4.A (F(X)=𝑏𝑥
, B> 0 , 𝑏 ≠ 1)
5.B (≠, <, >, ≤, ≥)
B.
6. FALSE
7. FALSE
8. TRUE
9. TRUE
10. TRUE

24. J. ADDITIONAL ACTIVITIES FOR APPLICATION OR REMEDIATION
ASSIGNMENT
A. DIRECTION: LIST DOWN AT LEAST THREE DIFFERENCES OF EXPONENTIAL EQUATION,
EXPONENTIAL INEQUALITIES AND EXPONENTIAL FUNCTION.
1.________________________________________________.
2.________________________________________________.
3.________________________________________________.
B. SEARCH AND LOOK FOR EXAMPLES ON HOW TO SOLVE EXPONENTIAL EQUATION AND
INEQUALITIES IN KHAN ACADEMY.NET, LRMDS, DEPED COMMONS OR ANY SOCIAL MEDIA
PLATFORMS.