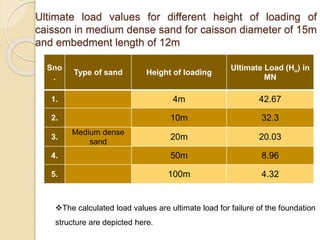
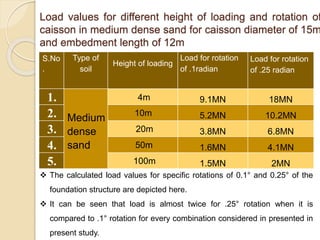
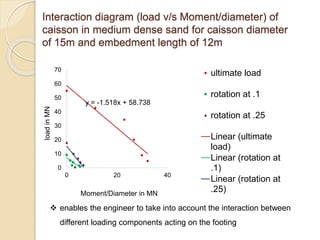
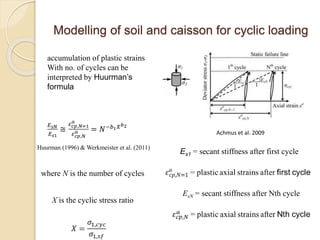
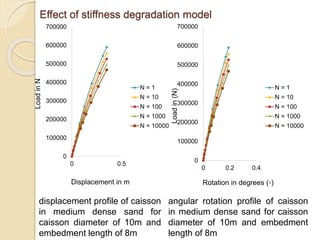
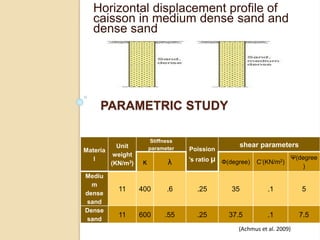
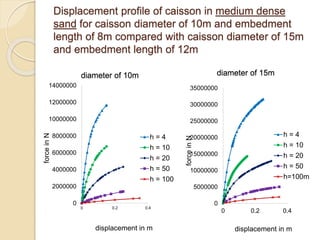
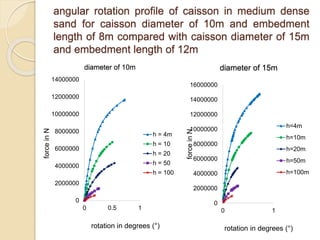
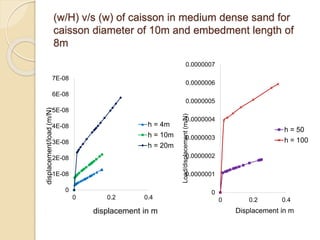
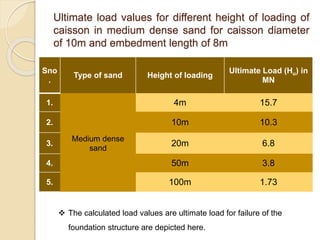
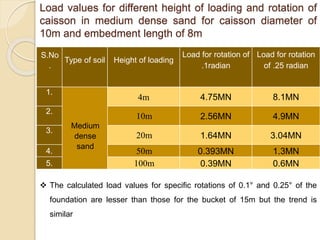
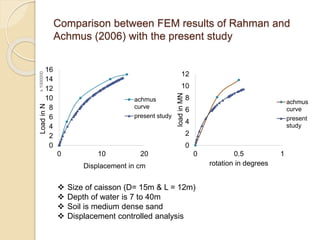
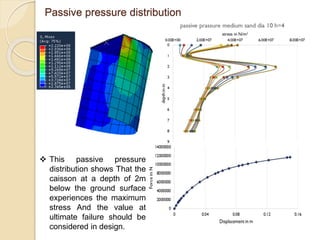
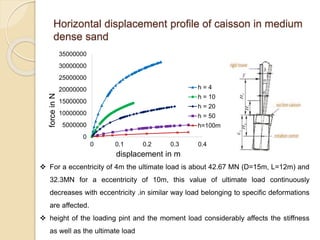
This document summarizes a study on the horizontal load-deformation behavior of suction caisson foundations. The study used finite element modeling in ABAQUS to simulate the behavior of caisson foundations in sandy soils under monotonic and cyclic loading conditions. Key findings included: (1) load capacity decreased with increased loading height and eccentricity, (2) maximum stresses occurred near the mid-depth of the caisson, and (3) stiffness degraded nonlinearly with increasing number of load cycles due to accumulated plastic strains. Parametric analyses looked at the effects of caisson diameter, soil type, and loading conditions. Conclusions focused on developing design methods for predicting load-moment interactions and capacity. Future work could consider clay soils

1. Horizontal Load – Deformation Behaviour of
Suction Caisson Foundations
Supervisor
Dr. Baleshwar Singh
Department of Civil Engineering
IIT Guwahati
Presented by
Pushkal Pratap
Roll No: 134104039

2. contents
 Cyclic loading
 Parametric study
 Conclusion
 Future work
 References
Introduction
Objective of study
Literature review.
Simulation of offshore
caisson foundation
monotonic loading
 Comparison of
results
 Passive pressure
distribution curves

3. Introduction
 Suction caissons or upturned buckets that
has been used in place of large diameter
piles for offshore structures for a depth of
15m to 40m.
 Subjected to lateral and vertical loads.
 Installed partially by self wt. and partially
by suction pressure.
 There are no accepted procedures, such
as API guidelines for piles.
 Analysis in the present study is done considering two critical aspects of
loading –
1) Long term drained loading limits of caisson response.
2) Caisson response after cyclic loading due to waves.
Houlsby, Ibsen & Byrne (2005)

4. Objective of study
 Objective is to study the behavior of suction bucket in sandy
and clayey soil deposits under different loading conditions
using FEM (finite element method) to develop interaction
diagrams based on load deformation curves using
commercial software ABAQUS 6.10
 Interaction diagram approach to bearing capacity estimation
for shallow footing enables the engineer to take into account
the interaction between different loading components acting
on footing.

5. MONOTONIC LOADING
Horizontal displacement profile of
caisson in medium dense sand

6. Modelling of soil and caisson for monotonic
loading
 For Simulation of the soil’s stress-strain-behavior following are provided in
the commercial software ABAQUS 6.10 -
1) Mohr-Coulomb failure criterion -
2) Elasto-Plastic material law -
.
This material law was extended in the
elastic range by taking a stress-
dependency of the oedometric modulus
of elasticity
Rahman and Achmus (2006)
Material
Unit
weight
(KN/m3)
Stiffness parameter Poission’s
ratio μ
shear parameters
ĸ λ Ф(degree) C’(KN/m2) Ψ(degree)
Medium
dense
sand
11 400 .6 .25 35 .1 5
(Achmus et al. 2009)

7. Comparison between FEM results of Rahman and
Achmus (2006) with the present study
0
2
4
6
8
10
12
0 0.5 1
load
in
MN
rotation in degrees
achmus
curve
present
study
0
2
4
6
8
10
12
14
16
0 10 20
Load
in
N
x
1000000
Displacement in cm
achmus
curve
present study
 Size of caisson (D= 15m & L = 12m)
 Depth of water is 7 to 40m
 Soil is medium dense sand
 Displacement controlled analysis

8. Passive pressure distribution
 This passive pressure
distribution shows That the
caisson at a depth of 2m
below the ground surface
experiences the maximum
stress And the value at
ultimate failure should be
considered in design.

9. Horizontal displacement profile of caisson in medium
dense sand
0
5000000
10000000
15000000
20000000
25000000
30000000
35000000
0 0.1 0.2 0.3 0.4
force
in
N
displacement in m
h = 4
h = 10
h = 20
h = 50
h=100m
 For a eccentricity of 4m the ultimate load is about 42.67 MN (D=15m, L=12m) and
32.3MN for a eccentricity of 10m, this value of ultimate load continuously
decreases with eccentricity .in similar way load belonging to specific deformations
are affected.
 height of the loading pint and the moment load considerably affects the stiffness
as well as the ultimate load

10. angular rotation profile of caisson in medium dense sand
for caisson diameter of 15m and embedment length of 12m
0
2000000
4000000
6000000
8000000
10000000
12000000
14000000
16000000
0 0.2 0.4 0.6 0.8
force
in
N
rotation in degrees (°)
h=4m
h=10m
h=20m
h=50m
h=100m
 Here a rotation of .25◦ which lies in the order of admissible rotations
for OWECs, is obtained at a loads of about 18MN (D=15m, L=12m)
and for an eccentricity of 4m and 10.2MN for an eccentricity of 10m
are obtained

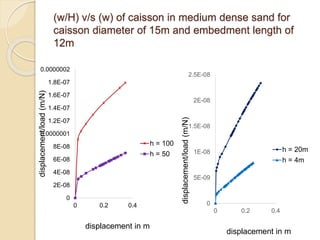
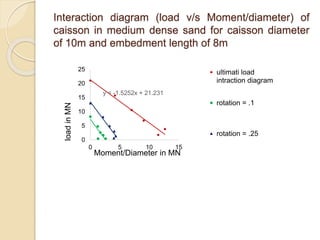
11. Estimation of ultimate load by Chin’s Method
• w/H versus w is plotted
The equation of the straight line can be represented as
w/H = C1 w + C2 (1)
• ultimate load Hu is then equal to
(H)ult = 1/C1 (2)
by Substituting equation (1) in (2) we get
H = [(h)ult w] / [w + (H)ult C2]

12. (w/H) v/s (w) of caisson in medium dense sand for
caisson diameter of 15m and embedment length of
12m
0
2E-08
4E-08
6E-08
8E-08
0.0000001
1.2E-07
1.4E-07
1.6E-07
1.8E-07
0.0000002
0 0.2 0.4
displacement/load
(m/N)
displacement in m
h = 100
h = 50
0
5E-09
1E-08
1.5E-08
2E-08
2.5E-08
0 0.2 0.4
displacement/load
(m/N)
displacement in m
h = 20m
h = 4m

13. Ultimate load values for different height of loading of
caisson in medium dense sand for caisson diameter of 15m
and embedment length of 12m
The calculated load values are ultimate load for failure of the foundation
structure are depicted here.
Sno
.
Type of sand Height of loading
Ultimate Load (Hu) in
MN
1. 4m 42.67
2. 10m 32.3
3.
Medium dense
sand
20m 20.03
4. 50m 8.96
5. 100m 4.32

14. Load values for different height of loading and rotation of
caisson in medium dense sand for caisson diameter of 15m
and embedment length of 12m
S.No
.
Type of
soil
Height of loading
Load for rotation
of .1radian
Load for rotation
of .25 radian
1.
Medium
dense
sand
4m 9.1MN 18MN
2. 10m 5.2MN 10.2MN
3. 20m 3.8MN 6.8MN
4. 50m 1.6MN 4.1MN
5. 100m 1.5MN 2MN
 The calculated load values for specific rotations of 0.1° and 0.25° of the
foundation structure are depicted here.
 It can be seen that load is almost twice for .25° rotation when it is
compared to .1° rotation for every combination considered in presented in
present study.

15. Interaction diagram (load v/s Moment/diameter) of
caisson in medium dense sand for caisson diameter
of 15m and embedment length of 12m
y = -1.518x + 58.738
0
10
20
30
40
50
60
70
0 20 40
load
in
MN
Moment/Diameter in MN
ultimate load
rotation at .1
rotation at .25
Linear (ultimate
load)
Linear (rotation at
.1)
Linear (rotation at
.25)
 enables the engineer to take into account the interaction between
different loading components acting on the footing

16. CYCLIC LOADING
Horizontal displacement profile of
caisson in medium dense sand

17. Modelling of soil and caisson for cyclic loading
Achmus et al. 2009
EsN = secant stiffness after Nth cycle
Es1 = secant stiffness after first cycle
accumulation of plastic strains
With no. of cycles can be
interpreted by Huurman’s
formula
Huurman (1996) & Werkmeister et al. (2011)
where N is the number of cycles
X is the cyclic stress ratio

18. Modelling of soil and caisson for cyclic loading
In Hurman’s formula degradation of stiffness can be described using two
material parameters b1 and b2
Soil type b1 b2 X
Medium dense sand 0.16 0.38
0.714
Dense sand 0.20 5.76
Huurman (1996) & Werkmeister et al. (2011)

19. Effect of stiffness degradation model
0
100000
200000
300000
400000
500000
600000
700000
0 0.5
Load
in
N
Displacement in m
N = 1
N = 10
N = 100
N = 1000
N = 10000
0
100000
200000
300000
400000
500000
600000
700000
0 0.2 0.4
Load
in
(N)
Rotation in degrees (◦)
N = 1
N = 10
N = 100
N = 1000
N = 10000
displacement profile of caisson
in medium dense sand for
caisson diameter of 10m and
embedment length of 8m
angular rotation profile of caisson
in medium dense sand for caisson
diameter of 10m and embedment
length of 8m

20. PARAMETRIC STUDY
Horizontal displacement profile of
caisson in medium dense sand and
dense sand
Materia
l
Unit
weight
(KN/m3)
Stiffness
parameter Poission
’s ratio μ
shear parameters
ĸ λ Ф(degree) C’(KN/m2)
Ψ(degree
)
Mediu
m
dense
sand
11 400 .6 .25 35 .1 5
Dense
sand
11 600 .55 .25 37.5 .1 7.5
(Achmus et al. 2009)

21. Displacement profile of caisson in medium dense
sand for caisson diameter of 10m and embedment
length of 8m compared with caisson diameter of 15m
and embedment length of 12m
0
2000000
4000000
6000000
8000000
10000000
12000000
14000000
0 0.2 0.4
force
in
N
displacement in m
diameter of 10m
h = 4
h = 10
h = 20
h = 50
h = 100
0
5000000
10000000
15000000
20000000
25000000
30000000
35000000
0 0.2 0.4
force
in
N
displacement in m
diameter of 15m
h = 4
h = 10
h = 20
h = 50
h=100m

22. angular rotation profile of caisson in medium dense
sand for caisson diameter of 10m and embedment
length of 8m compared with caisson diameter of 15m
and embedment length of 12m
0
2000000
4000000
6000000
8000000
10000000
12000000
14000000
0 0.5 1
force
in
N
rotation in degrees (°)
diameter of 10m
h = 4m
h = 10
h = 20
h = 50
h = 100
0
2000000
4000000
6000000
8000000
10000000
12000000
14000000
16000000
0 1
force
in
N
rotation in degrees (°)
diameter of 15m
h=4m
h=10m
h=20m
h=50m
h=100m

23. (w/H) v/s (w) of caisson in medium dense sand for
caisson diameter of 10m and embedment length of
8m
0
0.0000001
0.0000002
0.0000003
0.0000004
0.0000005
0.0000006
0.0000007
0 0.2 0.4
Load/displacement
(m/N)
Displacement in m
h = 50
h = 100
0
1E-08
2E-08
3E-08
4E-08
5E-08
6E-08
7E-08
0 0.2 0.4
displacement/load
(m/N)
displacement in m
h = 4m
h = 10m
h = 20m

24. Ultimate load values for different height of loading of
caisson in medium dense sand for caisson diameter
of 10m and embedment length of 8m
 The calculated load values are ultimate load for failure of the
foundation structure are depicted here.
Sno
.
Type of sand Height of loading
Ultimate Load (Hu) in
MN
1. 4m 15.7
2. 10m 10.3
3.
Medium dense
sand
20m 6.8
4. 50m 3.8
5. 100m 1.73

25. Load values for different height of loading and rotation of
caisson in medium dense sand for caisson diameter of
10m and embedment length of 8m
S.No
.
Type of soil Height of loading
Load for rotation of
.1radian
Load for rotation
of .25 radian
1.
Medium
dense
sand
4m 4.75MN 8.1MN
2.
10m 2.56MN 4.9MN
3.
20m 1.64MN 3.04MN
4. 50m 0.393MN 1.3MN
5. 100m 0.39MN 0.6MN
 The calculated load values for specific rotations of 0.1° and 0.25° of the
foundation are lesser than those for the bucket of 15m but the trend is
similar

26. Interaction diagram (load v/s Moment/diameter) of
caisson in medium dense sand for caisson diameter
of 10m and embedment length of 8m
y = -1.5252x + 21.231
0
5
10
15
20
25
0 5 10 15
load
in
MN
Moment/Diameter in MN
ultimati load
intraction diagram
rotation = .1
rotation = .25

27. conclusion
 In the study using monotonic loading the load-moment interaction for
the ultimate state can be described by nearly parallel straight lines for
a particular type of soil.
 Caisson under static monotonous loading behave as rigid piles with a
single point of rotation. The depth of point of rotation varies with the
type of soil and loading.
 Load carrying capacity has been varied with the type of soil and skirted
foundations are recommended for higher load resistance.
 With the help of passive pressure distribution diagrams it has been
found that the bucket is experiencing the maximum stress at .25L from
the top.

28. Future work
 Development of load interaction diagrams using load deformation
curves for clayey soil strata and a different soil model.
 Development of normalization curves for design of foundation
under wave loading.
 In the study pore water pressure is not considered it can also be
taken into account.
 Modulus of elasticity is also considered constant and variation of
modulus of elasticity with the deformation will be considered.
 Change in load deformation using other soil models can be
considered.
 Liquefaction due to cyclic loading .

29. References
 ABAQUS, (2010). “User’s manual, version 6.10 simuilia.” Dassault Systemes Simulia
Corp, Providence, RI.
 X. B. L, J. H. Zhang, S. Y. Wang, G.L. Sun and Z.M. Shi, “Experimental study of the pore
pressure and deformation of suction bucket foundations under horizontal dynamic
loading,” Chinese Ocean Eng. vol. 19, No. 4, pp. 671-680, 2005.
 X.B. Lu, Y.R. Wu and B.T. Jiao, “Centrifugal experimental study of suction bucket
foundations under dynamic loading,” ACTA Mech. Sin., vol. 23, pp. 689-698, 2007.
 W. Dyme and G.T. Houlsby, “Drained behavior of suction caisson on very dense sand,”
In: Proc. Offshore Technol. Conf., Houston, OTC10994, 1998, pp. 765-782.
 B.W. Byrne and G.T. Houlsby, “Experimental investigations of the responses of suction
caissons to transient combined loading,” ASCE J. Geotech. Geoenviron. Eng., vol. 130,
No. 3, pp. 240-253, 2004
 Ibsen, L.B., Schakenda, B., Nielsen, S.A. (2003) “Development of bucket foundation for
offshore wind turbines, a novel principle”. Proc. USA Wind 2003 Boston.
 House, A. (2002) “Suction Caisson Foundations for Buoyant Offshore Facilities”, PhD
Thesis, the University of Western Australia
 Byrne, B.W., Houlsby, G.T. and Martin, C.M. (2002a) “Cyclic Loading of Shallow Offshore
Foundations on Sand”, Proc. Int. Conf on Physical Modelling in Geotech., July 10–12, St
John’s, Newfoundland, 277–282
 Lars Bo Ibsen, Morten Liingaard and Lars Andersen (2006), "Dynamic stiffness of suction
caisson foundation"ISSN 1901-726X DCE Technical Report No. 7
 Ibsen, L.B., Schakenda, B., Nielsen, S.A. (2003) “Development of bucket foundation for
offshore wind turbines, a novel principle”. Proc. USA Wind 2003 Boston.

30. Thank you