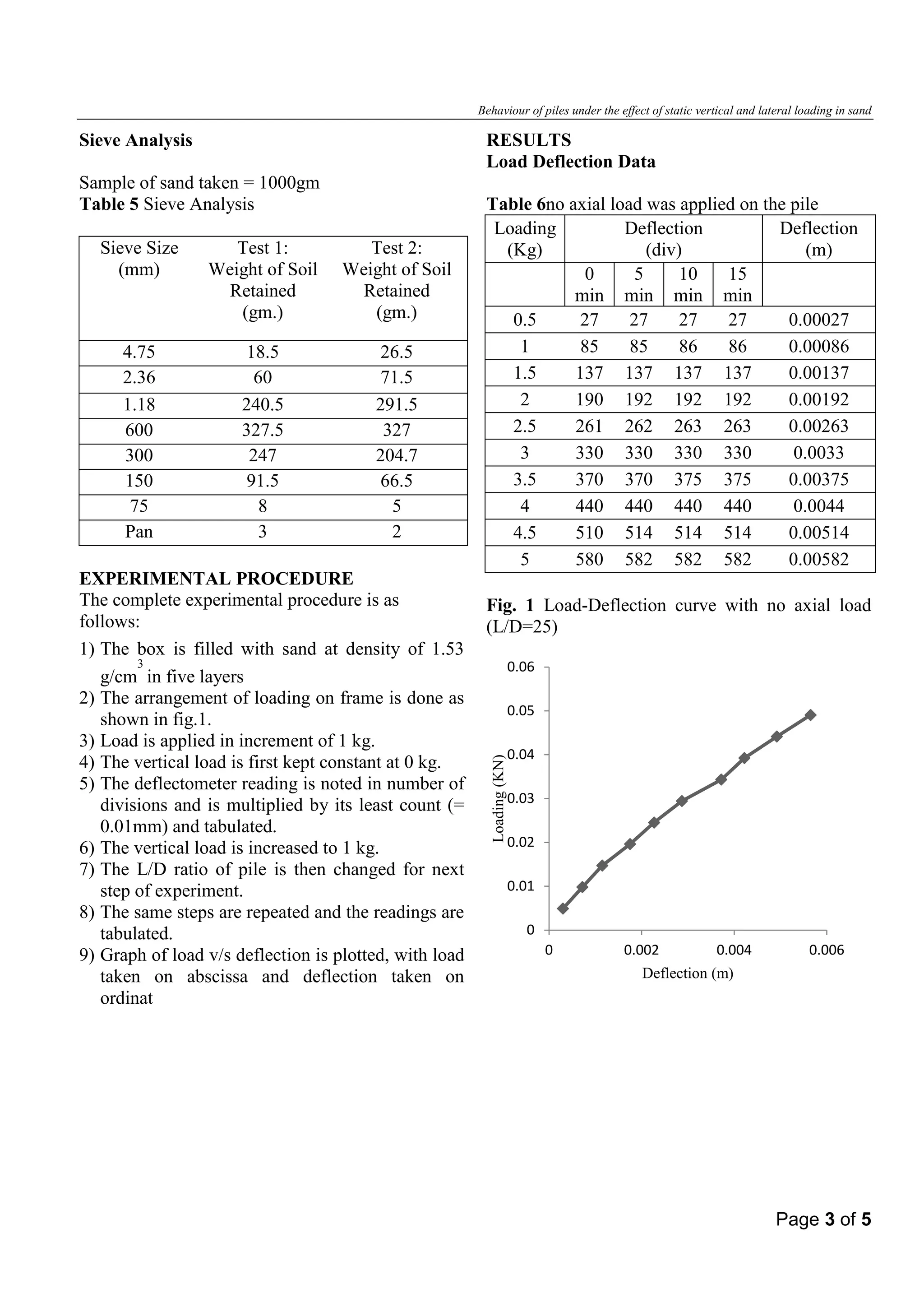
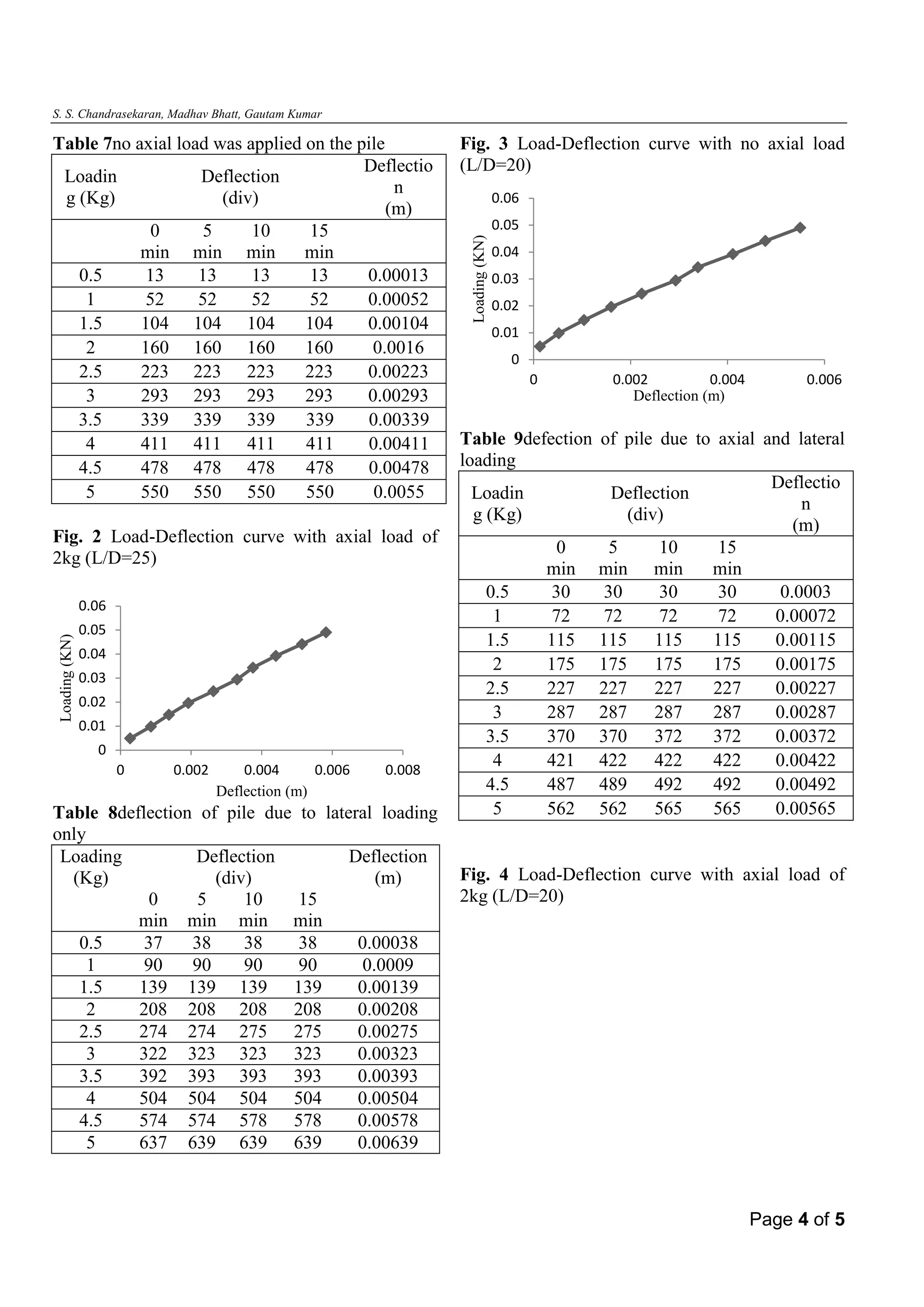
The document summarizes an experimental study on the behavior of piles under static vertical and lateral loading in sand. Pile load tests were conducted with model PVC piles installed in a sand-filled box. Piles were loaded with different vertical and lateral loads and deflections were measured. Results show that lateral deflection decreases with increasing pile length-to-diameter ratio and when a vertical load is applied. Load-deflection curves are presented and conclusions are that vertical loading reduces lateral deflection of the pile and increased L/D ratio also decreases lateral deflection. The study provides data on pile behavior under combined loading conditions in sand.

1. Proceedings of Indian Geotechnical Conference
December 22-24,2013, Roorkee
BEHAVIOUR OF PILES UNDER THE EFFECT OF STATIC VERTICAL AND LATERAL LOADING IN SAND
S. S. Chandrasekaran, Associate Professor, SMBS, VIT University. chandrasekaran.ss@vit.ac.in
M. Bhatt, Student, School of Mechanical and Building Sciences, VIT University. madhav.bhatt31@gmail.com
G. Kumar,Student, School of Mechanical and Building Sciences, VIT University. gaumji22@gmail.com
ABSTRACT: This project reports on the behaviour of single pile due to both vertical and horizontal load applied directly. The cohesionless soil (sandy) was taken and tests were performed on it to find out the property of soil. The sand was filled in the box in five layers (each layer of depth 170mm), each layer compacted using hammer. The pile is then fixed as per the required L/D ratio. The vertical and horizontal load tests were performed and deflection was found using mechanical dial gauges. The curve was drawn and behaviour of pile was found under different vertical and horizontal load.
INTRODUCTION
Pile foundations are the part of a structure used to carry and transfer the load of the structure to the bearing ground located at some depth below ground surface. The main components of the foundation are the pile cap and the piles. Piles are long and slender members which transfer the load to deeper soil or rock of high bearing capacity avoiding shallow soil of low bearing capacity. The main types of materials used for piles are wood, steel and concrete. Piles made from these materials are driven, drilled or jacked into the ground and connected to pile caps.
Piles are frequently subjected to lateral forces and moments viz., i) quay and harbor structures in which horizontal forces are generated due to the impact of ships during berthing and wave action, ii) offshore structures subjected to wind and wave action, iii) tall structures like chimneys, transmission towers subjected to wind loads and iv) in structures situated in earthquake prone areas. In the design of such pile foundations, not only the ultimate loads shall be worked out to arrive at the safe loads but also the deflections need to be worked out. Matlock and Reese (1960)[1] presented a generalized iterative solution method for rigid and flexible laterally loaded piles embedded in soils with two forms of varying modulus with depth. Davisson and Gill (1963)[2] investigated the case of a laterally loaded pile embedded in a layered soil system with a constant (but different) modulus of subgrade reaction in each layer. Broms (1964a, b)[3,4] method is also based on earth pressure theory with simplifying assumption for distribution of ultimate soil resistance along the pile length and this method is applicable for both short piles and long piles. Randolph (1981)[5] studied the problem of flexible piles under lateral loading and proposed algebraic expressions for pile head displacement and rotation.
METHODOLOGY
Wooden Box arrangement
Setup consists of a box made from ply of 6mm thickness having dimension 640mm X 750mm X 850mm. This box is filled with sand in 5 layers. Each layer with a thickness of 170mm. After one layer is filled, it is compacted with to get the required height which was calculated taking in consideration the required density of the sand.
Pulley Arrangement
A wooden frame was fabricated to support the pulley system. Height of the frame is 1000mm, and the bottom support is given by three legs on each side of the frame. A hook is attached to the pile cap at its centre and also at the centre of the frame top flange. A wire is made to pass through this hooks Page 1 of 5

2. S. S. Chandrasekaran, Madhav Bhatt, Gautam Kumar
and the pulley is suspended on the frame. The extension of the wire serves the purpose to support the weights.
Deflectometer Arrangement
The deflectometer is placed behind the pile cap. The needle is first pressed in and then the magnetic base is attached to a sheet metal box placed on the soil layer. The readings are noted down as the needle is released due to pile movement on loading. The error due to weight of brick placed on sheet metal box is negligible when the soil consolidation is measured.
Pile
PVC is used as the pile material. The pile under study is a floating/friction pile and hence the clearance from the bottom of the box is 250mm. the diameter of the pile is 32mm and length is 800mm. the pile is placed centrally before the sand filling is done in order to minimize the disturbance produced by driven pile to soil. It is attached to a wooden pile cap at the centre.
Pile Cap
The pile cap is fabricated from a wooden block of 20mm thickness. It is square in shape with sides of 95mm. a hole is cut out in at its centre to allow the pile to fit. A hole is drilled at one of its side for attaching the hook where load can be applied.
Model Pile
In the present experimental investigations, model pile material and its dimensions are selected adhering to the following similitude law proposed by Wood et al (2002):
m4.51ImppEEIn=
Equation 1
Em = modulus of elasticity of model pile,
Ep = modulus of elasticity of prototype pile,
Im = moment of inertia of model pile,
Ip = moment of inertia of prototype pile and
1/n = scale factor for length.
SOIL TESTS
Relative Density Test
Relative density is defined by the following formula:
()minmaxmaxmindrdD ρρρρρρ − =−
Equation 2
For determination of minimum dry density ρmin, a representative oven dry sample of soil is taken. The sample is then pulverized and sieved. The minimum dry density is found by pouring the dry sand in mould using a pouring device. The spout of the pouring device is so adjusted that the height of the fall is always 25mm. the mass and the volume of the soil deposited are found, and the dry density of the soil is determined.
The maximum dry density is determined by dry method. In this method, the mould is filled with thoroughly mixed oven-fry soil. A surcharge load is placed on the soil surface, and the mould is fixed to a vibrator deck. The specimen is vibrated for 8 minutes. The mass and volume of the soil in the compacted state are found. The maximum is then found.
Mould height = 170mm
Diameter = 150mm
3max1.71/gcmγ=
3min1.53/gcmγ=
Direct Shear Test
31.57/dgcmγ=
Specific Gravity Test
The specific gravity of a soil sample is given by the following formula:
Equation 3 ()(){} 212134MMGMMMM− = −−−
Where:
M1 = mass of empty pycnometer
M2 = mass of pycnometer and dry soil
M3 = mass of pycnometer, soil and water
M4 = mass of Pycnometer filled with water
G = 2.60
Page 2 of 5

3. Behaviour of piles under the effect of static vertical and lateral loading in sand
Sieve Analysis
Sample of sand taken = 1000gm
Table 5 Sieve Analysis
Sieve Size
(mm)
Test 1:
Weight of Soil Retained
(gm.)
Test 2:
Weight of Soil Retained
(gm.)
4.75
18.5
26.5
2.36
60
71.5
1.18
240.5
291.5
600
327.5
327
300
247
204.7
150
91.5
66.5
75
8
5
Pan
3
2
EXPERIMENTAL PROCEDURE
The complete experimental procedure is as follows:
1) The box is filled with sand at density of 1.53 g/cm3 in five layers
2) The arrangement of loading on frame is done as shown in fig.1.
3) Load is applied in increment of 1 kg.
4) The vertical load is first kept constant at 0 kg.
5) The deflectometer reading is noted in number of divisions and is multiplied by its least count (= 0.01mm) and tabulated.
6) The vertical load is increased to 1 kg.
7) The L/D ratio of pile is then changed for next step of experiment.
8) The same steps are repeated and the readings are tabulated.
9) Graph of load v/s deflection is plotted, with load taken on abscissa and deflection taken on ordinat
RESULTS
Load Deflection Data
Table 6no axial load was applied on the pile
Loading (Kg)
Deflection
(div)
Deflection
(m)
0 min
5 min
10 min
15 min
0.5
27
27
27
27
0.00027
1
85
85
86
86
0.00086
1.5
137
137
137
137
0.00137
2
190
192
192
192
0.00192
2.5
261
262
263
263
0.00263
3
330
330
330
330
0.0033
3.5
370
370
375
375
0.00375
4
440
440
440
440
0.0044
4.5
510
514
514
514
0.00514
5
580
582
582
582
0.00582
Fig. 1 Load-Deflection curve with no axial load (L/D=25)
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.002
0.004
0.006
Loading (KN)
Deflection (m)
Page 3 of 5

4. S. S. Chandrasekaran, Madhav Bhatt, Gautam Kumar
Table 7no axial load was applied on the pile
Loading (Kg)
Deflection
(div)
Deflection
(m)
0 min
5
min
10 min
15
min
0.5
13
13
13
13
0.00013
1
52
52
52
52
0.00052
1.5
104
104
104
104
0.00104
2
160
160
160
160
0.0016
2.5
223
223
223
223
0.00223
3
293
293
293
293
0.00293
3.5
339
339
339
339
0.00339
4
411
411
411
411
0.00411
4.5
478
478
478
478
0.00478
5
550
550
550
550
0.0055
Fig. 2 Load-Deflection curve with axial load of 2kg (L/D=25)
Table 8deflection of pile due to lateral loading only
Loading (Kg)
Deflection
(div)
Deflection
(m)
0 min
5 min
10 min
15 min
0.5
37
38
38
38
0.00038
1
90
90
90
90
0.0009
1.5
139
139
139
139
0.00139
2
208
208
208
208
0.00208
2.5
274
274
275
275
0.00275
3
322
323
323
323
0.00323
3.5
392
393
393
393
0.00393
4
504
504
504
504
0.00504
4.5
574
574
578
578
0.00578
5
637
639
639
639
0.00639
Fig. 3 Load-Deflection curve with no axial load (L/D=20)
Table 9defection of pile due to axial and lateral loading
Loading (Kg)
Deflection
(div)
Deflection
(m)
0 min
5
min
10 min
15 min
0.5
30
30
30
30
0.0003
1
72
72
72
72
0.00072
1.5
115
115
115
115
0.00115
2
175
175
175
175
0.00175
2.5
227
227
227
227
0.00227
3
287
287
287
287
0.00287
3.5
370
370
372
372
0.00372
4
421
422
422
422
0.00422
4.5
487
489
492
492
0.00492
5
562
562
565
565
0.00565
Fig. 4 Load-Deflection curve with axial load of 2kg (L/D=20)
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.002
0.004
0.006
0.008
Loading (KN)
Deflection (m)
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.002
0.004
0.006
Loading (KN)
Deflection (m)
Page 4 of 5

5. Behaviour of piles under the effect of static vertical and lateral loading in sand
CONCLUSIONS
From the findings taken from all the experimental data and by plotting their respective load-deflection curves, we can conclude that the slope of the plot decreases. Practically, this states that as the vertical load on a pile is applied, it resists the movement due to lateral loading. As such, the ratio of vertical load applied, to lateral load, in actual cases is much larger than that can be reproduced in laboratory condition. Hence, piles supporting large load of a building undergoes minimum lateral displacement.
From the graph and the deflection data, it is also observed that as the L/D ratio of Pile increases, the lateral deflection of the pile head decreases.
REFERENCES
1. Matlock, H., and Reese, L. C. (1960). "Generalized solutions for laterally loaded
piles." J. Soil Mech. and Found. Div., ASCE, 86(5), 63-91.
2. Davisson, M. and Gill, H. (1963). “Laterally loaded piles in a layered system.” Journal of the Soil Mechanics and Foundations Division, ASCE, 89, 63 – 94.
3. Broms, B. B. (1964a): "Lateral Resistance of Piles in Cohesive Soils", Journal of the Soil Mechanics and Foundation Division, ASCE, 90, pp. 27 – 63.
4. Broms, B. B. (1964b). “Design of laterally loaded piles.” Journal of the Soil Mechanics and Foundation Division, ASCE, 90, 123-156.
5. Randolph, M. F. (1981). “The response of flexible piles to lateral loading.” Geotechnique, 31(2), 247-259.
6. Wood, D. M., Crewe, A. and Taylor, C. (2002). “Shaking table testing of geotechnical models.” International Journal of Physical Modelling in Geotechnics, 1, 1- 13.
• Figures 1-4 shows the load deflection curve for L/D ratio of 20 and 25 and with and without axial loading.
• Table 1-4shows the measurements to find the relative density of the soil.
• Table 5 Sieve Analysis test results.
• Table 6-9 Deflection measurements taken on pile.
• Equation 1 shows the way to compute dimension of model pile
• Equation 2 shows the formula to compute
• relative density.
• Equation 3 shows the formula to compute specific gravity
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.002
0.004
0.006
Loading (KN)
Deflection (m) Page 5 of 5