This document discusses arithmetic coding techniques for generating binary codes to represent sequences. It provides: 1) An overview of arithmetic coding, which is a lossless data compression technique that generates variable-length binary codes based on symbol probabilities. 2) Formulas and steps for encoding a sample sequence using arithmetic coding, calculating lower and upper bounds at each step based on cumulative distribution functions. 3) An example decoding a binary code back to the original sequence, calculating bounds and rescaling at each step.

1. Information Technology Department
Active Learning Assignment
Akshay Patel (150120116051)
Prof. Alpa Oza
1

2. BINARY CODE
 We went to find a binary code that will represent the
sequence X in a unique and efficient manner.
 Arithmetic coding is lossless data compression
technique for generating binary code.
 Algorithm Implementation is also the another technique
which is use to generate the binary code.
 It is variable length coding.
 Requires knowledge of symbol probabilities.
 CDF:- Commutative Distributive Function
2

3.  ln = ln-1 + (un-1 - ln-1) * Fx (xn-1)
 un = ln-1 + (un-1 - ln-1) * Fx (xn)
Where,
 ln → Lower limit after considering nth symbol.
 un → Upper limit after considering nth symbol.
 ln-1 → Lower limit before considering nth symbol.
 un-1 → Upper limit before considering nth symbol.
 Fx (xn) → CDF of nth symbol
 Fx (xn-1) → CDF of symbol before nth symbol
 Range = High – Low
 High = Low + Range * Highrange(C)
 Low = Low + Range * Lowrange(C)
FORMULA:- ENCODING
3

4.  We wish to encode the sequence “1321”
P(1)=0.8, P(1)=0.02, P(1)=0.18
 First element is 1
Range = H – L =1–0 =1
Low = L + R*L =0+1*0 =0
High = L + R*H =0+1*0.8 =0.8
EXAMPLE
1
(0.8)
2
(0.02)
3
(0.18)
1
0
4

5. 1
(0.8)
2
(0.02)
3
(0.18)
1
0 0
0.8
 Second element is 3
Range = H – L =0.8-0 =0.8
Low = L + R*L =0+0.8*0.82 =0.656
High = L + R*H =0+0.8*1 =0.8
5

6.  Third element is 2
Range = H – L =0.8-0.656 =0.144
Low = L + R*L =0.656+0.144*0.8 =0.7712
High = L + R*H =0.656+0.144*0.82 =0.77408
1
(0.8)
2
(0.02)
3
(0.18)
1
0 0
0.8
0.656
0.8
6

7.  Last element is 1
Range = H – L =0.77408-0.7712 =0.00288
Low = L + R*L =0.7712+0.00288*0 =0.7712
High = L + R*H =0.7712+0.00288*0.8 =0.773504
 Tag value = (H+L)/2 = 0.772352
1
(0.8)
2
(0.02)
3
(0.18)
1
0 0
0.8
0.656
0.8
0.7712
0.77408
0.7712
0.773504
7

8. ALGORITHM IMPLEMENTATION
 ln = ln-1 + (un-1 - ln-1) * Fx (xn-1)
 un = ln-1 + (un-1 - ln-1) * Fx (xn)
 E1 = [0.0,5) → [0,1); E1(x) = 2x
 E2 = [0.5,1) → [0,1); E2(x) = 2(x-0.5)
 [l(n), u(n)] ᴄ [0.0,5) →0, Then perform E1 Rescale
 [l(n), u(n)] ᴄ [0.5,1) →1, Then perform E2 Rescale
 l(n) ϵ [0.0,5) , u(n) ϵ [0.5,1) → Output Undetermined
8

9. EXAMPLE
 ln = ln-1 + (un-1 - ln-1) * Fx (xn-1)
 un = ln-1 + (un-1 - ln-1) * Fx (xn)
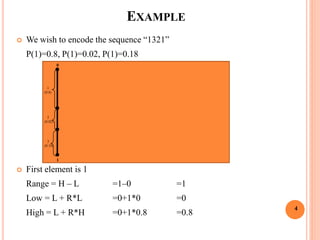
 First element is 1
 l=0+(1-0)*0 =0
 h=0+(1-0)*0.8 =0.8
 [l(n), u(n)] = [0,0.8) So, Output Undetermined
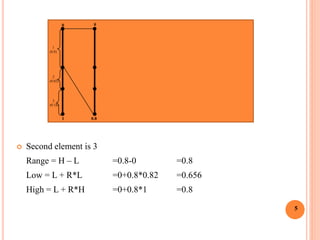
 Second element is 3
 l=0+(0.8-0)*0.82 =0.656
 h=0+(0.8-0)*1 =0.8
[0.656,0.8) ᴄ [0.5,1) So, Transmit 1 and Rescale by E2
 l=2(x-0.5) =2(0.656-0.5) =0.312
 h=2(x-0.5) =2(0.8-0.5) =0.6
[0.312,0.6) So, Output Undetermined
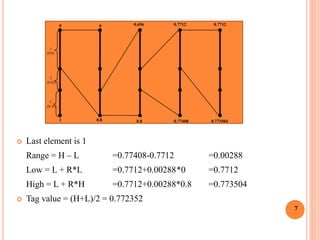
1
(0.8)
2
(0.02)
3
(0.18)
10
9

10.  Third element is 2
 l=0.312+(0.6-0.312)*0.8 =0.5424
 h=0312+(0.6-0.312)*0.82 =0.54816
[0.5424, 0.54816) ᴄ [0.5,1) So, Transmit 1 and Rescale by E2
 l=2(0.5424 -0.5) =0.0848
 h=2(0.54816 -0.5) =0.09632
[0.0848, 0.09632) ᴄ [0,0.5) So, Transmit 0 and Rescale by E
 l=2(0.0848) =0.1696
 h=2(0.09632) =0.19264
[0.1696, 0.19264) ᴄ [0,0.5) So, Transmit 0 and Rescale by E
 l=2(0.1696) =0.3392
 h=2(0.19264) =0.38528
[0.3392, 0.38528) ᴄ [0,0.5) So, Transmit 0 and Rescale by E
10

11.  l=2(0.3392) =0.6784
 h=2(0.38528) =0.77056
[0.6784, 0.77056) ᴄ [0.5,1) So, Transmit 1 and Rescale by E2
 Third element is 2
 l=2(0.6784-0.5) =0.3568
 h=2(0.77056-0.5) =0.54112
[0.3568, 0.54112) Output Undetermined
 Last element is 1
 l=0.3568+(0.54112-0.3568)*0 =0.3568
 h=0.3568+(0.54112-0.3568)*0.8 =0.504256
[0.3568, 0.504256) Output Undetermined
 Answer = 110001
11

12.  Six bit of Tag value = 110001 → 0.765625
 0.765625 is in range of 1 so first element is 1.
 l=0.+(1-0)*0 =0
 h=0+(1-0)*0.8 =0.8
[0, 0.8) Undetermined
 So the tag value is t*=(tag - l(k-1))/(u(k-1) -l(k-1))
=(0.765625-0)/(0.8-0)
=0.9579
 0.9579 is in range of 3 so second element is 3.
 l=0+(0.8-0)*0.82 =0.656
 h=0+(0.8-0)*1 =0.8
 [0.656, 0.8) ᴄ [0.5,1) So, Rescale by E2
 l=2(0.656-0.5) =0.656
 h=2(0.8-0.5) =0.8
[0.656, 0.8) Undetermined
DECODING

13.  Six bit of Tag value = 100011 → 0.546875
 So the tag value is t*=(tag - l(k-1))/(u(k-1) -l(k-1))
=(0.546875-0.312)/(0.6-0.312)
=0.8155
 0.8155 is in range of 2 so third element is 2.
 l=0.312+(0.6-0.312)*0.8 =0.5424
 h=0.312+(0.6-0.312)*0.82 =0.54816
 [0.5424, 0.54816) ᴄ [0.5,1) So, Rescale by E2
 l=2(0.5424-0.5) =0.0848
 h=2(0.54816-0.5) =0.09632
 [0.0848, 0.09632) ᴄ [0,0.5) So, Rescale by E1
 l=2(0.0848) =0.1696
 h=2(0.09632) =0.19264

14.  [0.1696, 0.19264) ᴄ [0,0.5) So, Rescale by E1
 l=2(0.1696) =0.3392
 h=2(0.19264) =0.38528
 [0.3392,0.38528) ᴄ [0,0.5) So, Rescale by E1
 l=2(0.3392) =0.6784
 h=2(0.38528) =0.77056
 [0.6784, 0.77056) ᴄ [0.5,1) So, Rescale by E2
 l=2(0.6784-0.5) =0.3568
 h=2(0.77056-0.5) =0.54112
[0.3568, 0.54112) Undetermined
 Six bit of Tag value = 100000 → 0.5
 So the tag value is t*=(tag - l(k-1))/(u(k-1) -l(k-1))
=(0.5-0.3568)/(0.54112-0.3568)
=0.72690972
 0.72690972 is in range of 1 so last element is 1.
 So the answer is 1321

15. REFERENCES
 Book
15

16. 16