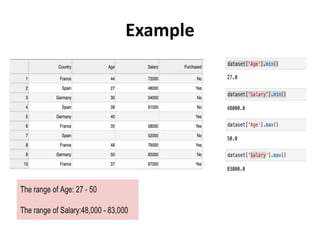
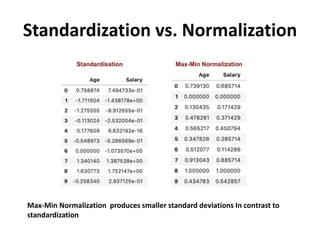
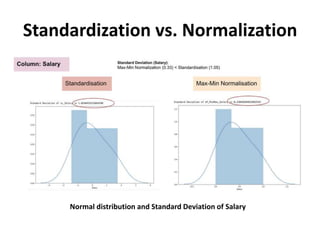
The document discusses data transformation techniques, specifically focusing on standardization and normalization, which are crucial for feature scaling in machine learning. It outlines the differences between these methods, their appropriate applications, and their impacts on datasets with varying scales, particularly emphasizing the importance of scaling in distance-based models. Standardization is noted for being more robust to outliers, while normalization is easier to apply but less effective in their presence.

1. Data Transformation –
Standardization & Normalization

2. Data Transformation
• Data transformation is one of the fundamental
steps in the part of data processing
• The technique of feature scaling includes the
terms scale, standardize, and normalize
• The key issues are –
– the difference between Standardization and
Normalization
– when to use Standardization and when to use
Normalization
– how to apply feature scaling in Python/R

3. Feature Scaling
• Different types of variables in the same dataset is quite
common
• A significant issue - the range of the variables may
differ a lot
• Using the original scale - may put more weights on the
variables with a large range
• To deal with this problem, - apply the technique of
features rescaling to independent variables or features
of data in the step of data pre-processing
• The terms normalization and standardization are
sometimes used interchangeably, but they usually refer
to different things

4. Feature Scaling
• The goal of applying Feature Scaling is to make
sure features are on almost the same scale so
that each feature is equally important and
make it easier to process by most ML
algorithms

5. Example

6. Example
• This is a dataset that contains an independent variable
(Purchased) and 3 dependent variables (Country, Age,
and Salary)
• Variables are not on the same scale because the range
of Age is from 27 to 50, while the range of Salary going
from 48 K to 83 K
• The range of Salary is much wider than the range
of Age
• This will cause some issues –
– a lot of machine learning models such as k-means
clustering and nearest neighbour classification are based
on the Euclidean Distance

7. Example
Issues-
• Euclidean distance will be dominated by the salary
• The difference in Age contributes less to the overall difference
• Thus
• Must apply Feature Scaling to bring all values to the same
magnitudes
• To do this - primarily two methods are Standardization and
Normalization

8. Standardization
• Standardization or Z-Score Normalization is
the transformation of features by subtracting
from mean and dividing by standard
deviation.
• This is often called as Z-score

9. Standardization
• Standardization can be helpful in cases where the
data follows a Gaussian distribution, however,
this does not have to be necessarily true
• Geometrically - it translates the data to the mean
vector of original data to the origin and squishes
or expands the points if std dev is 1 respectively
• The shape of the distribution is not affected – as
this transforms a normal distribution to a
standard normal distribution
• Standardization - not affected by outliers as there
is no predefined range of transformed features

10. Normalization
• Normalization or Min-Max Scaling is used to
transform features to be on a similar scale
• This technique is to re-scales features between 0
and 1.
• For every feature, the minimum value gets
transformed into 0, and the maximum value gets
transformed into 1

11. Standardization vs. Normalization
Max-Min Normalization produces smaller standard deviations In contrast to
standardization

12. Standardization vs. Normalization
Normal distribution and Standard Deviation of Salary

13. Standardization vs. Normalization
Normal distribution and Standard Deviation of Age

14. Standardization vs. Normalization
• From the above graphs, it is quite clear that applying
Max-Min Nomaralization in this dataset has generated
smaller standard deviations (Salary and Age) than using
Standardization method. It implies the data are more
concentrated around the mean if data is scaled using
Max-Min Nomaralization.
• As a result, if you have outliers in your feature
(column), normalizing your data will scale most of the
data to a small interval, which means all features will
have the same scale but does not handle outliers well.
Standardization is more robust to outliers, and in many
cases, it is preferable over Max-Min Normalization.

15. Standardization vs. Normalization
Normalization Standardization
Minimum and maximum value of features
are used for scaling
Mean and standard deviation is used for
scaling.
It is used when features are of different
scales.
It is used when we want to ensure zero
mean and unit standard deviation.
Scales values usually between [0, 1] It is not bounded to a certain range.
It is really affected by outliers. It is much less affected by outliers.
This transformation squishes the n-
dimensional data into an n-dimensional
unit hypercube.
It translates the data to the mean vector of
original data to the origin and squishes or
expands.
It is useful when we don’t know about the
distribution
It is useful when the feature distribution is
Normal or Gaussian.
It is a often called as Scaling Normalization It is a often called as Z-Score Normalization.

16. When Feature Scaling Matters
• Some machine learning models are
fundamentally based on distance matrix, also
known as the distance-based classifier - K-
Nearest-Neighbours, SVM, and Neural Network
• Feature scaling is extremely essential to those
models, especially when the range of the features
is very different
• Otherwise, features with a large range will have a
large influence in computing the distance.

17. When Feature Scaling Matters
• Max-Min Normalization typically allows us to transform
the data with varying scales so that no specific
dimension will dominate the statistics, and it does not
require making a very strong assumption about the
distribution of the data, such as k-nearest neighbours
and artificial neural networks
• However, Normalization does not treat outliners very
well. On the contrary, standardization allows users to
better handle the outliers and facilitate convergence
for some computational algorithms like gradient
descent. Therefore, we usually prefer standardization
over Min-Max Normalisation.