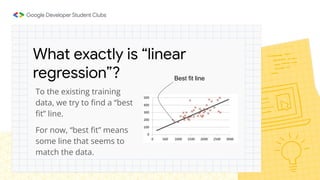
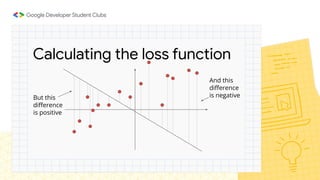
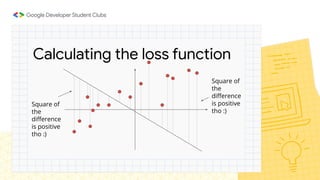
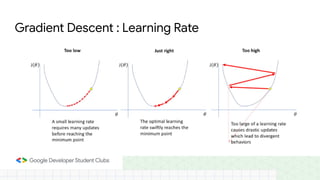
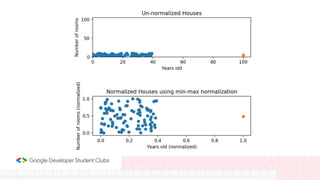
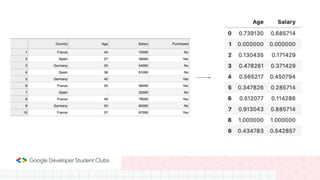
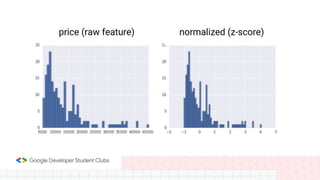
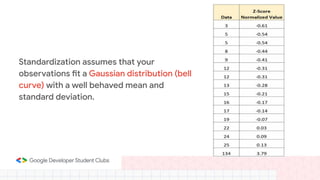
This document provides an overview of linear regression and logistic regression concepts. It begins with an introduction to linear regression, discussing finding the best fit line to training data. It then covers the loss function and gradient descent optimization algorithm used to minimize loss and fit the model parameters. Next, it discusses logistic regression for classification problems, covering the sigmoid function for hypothesis representation and interpreting probabilities. It concludes by discussing feature scaling techniques like normalization and standardization to prepare data for modeling.

1. Welcome to
Explore ML!
Day 2

2. Linear Regression
Fitting Linear Models

3. Premise
What are we trying to achieve?
We are trying to solve or
predict something, based on
what we already know.
This is a regression problem,
that is, we want predict a real
valued output.
?

4. What exactly is “linear
regression”?
To the existing training
data, we try to find a “best
fit” line.
For now, “best fit” means
some line that seems to
match the data.
Best fit line

6. This is an example of
___________

7. This is an example of
Supervised Learning

8. Recall your high school
math classes.
y = mx + c
Model parameters :
Model Representation

11. Tweaking the value of the parameters

13. Loss function
Formalizing the notion of best fit line
How exactly do you say one line fits better than the
other?
Let’s look at what exactly is loss and the loss function.

14. Loss function
H(xi
) - yi

15. Loss function
Oops,
Looks like
the errors
became
bigger

16. Calculating the loss function
Add all the
differences
between
predicted
values and
our data
points

17. Calculating the loss function
But this
difference
is positive
And this
difference
is negative

18. Calculating the loss function
Square of
the
difference
is positive
tho :)
Square of
the
difference
is positive
tho :)

19. The math
Calculating the loss function
In fact this idea applies for all machine learning model
The aim is to find parameters for which is minimum.

20. This function is the reason why models can learn things. It makes the
model descend the gradient of errors to reach a place of perfection. It
involves some mathematical calculation to minimize the error between
the actual value and the predicted value.
Optimization Algorithm
Gradient Descent

21. Gradient Descent : Intuition

22. Gradient Descent : Algorithm

23. Gradient Descent : Algorithm

24. Gradient Descent : Math

25. Gradient Descent : Learning Rate

26. Feature Scaling

27. Most of the real-life datasets that you will be dealing with will have
many features ranging from a wide range of values.

28. If you were asked to predict the price of a house, you will be provided
with a dataset with multiple features like no.of. bedrooms, square feet
area of the house, etc.
There’s a problem though.
For example,

29. The range of data in each feature will vary wildly.
For example, the number of bedrooms can vary from, say, 1 to 5 and
square feet area can range from 500 to 3000.
How is this a problem?

32. How do you solve this?

33. Feature Scaling

34. Feature Scaling is a data preprocessing step used to normalize the
features in the dataset to make sure that all the features lie in a similar
range.
It is one of the most critical steps during the pre-processing of data
before creating a machine learning model.

35. If a feature’s variance is orders of magnitude more than the variance of
other features, that particular feature might dominate other features in
the dataset, which is not something we want happening in our model.
Why?

36. Two important scaling techniques:
1. Normalisation
2. Standardisation

37. Normalisation

39. Normalization is the concept of scaling the range of values in a feature
between 0 to 1.
This is referred as Min-Max Scaling.

40. Min-Max Scaling

42. Standardisation

44. Standardisation is a scaling technique where the values are centered
around the mean with a unit standard deviation.
Standardisation is required when features of input data set have large
differences between their ranges, or simply when they are measured in
different measurement units, i.e. kwh, Meters, Miles and more.

45. Z-score is one of the most popular methods to standardise data, and
can be done by subtracting the mean and dividing by the standard
deviation for each value of each feature.

47. Standardization assumes that your
observations fit a Gaussian distribution (bell
curve) with a well behaved mean and
standard deviation.

48. In conclusion,
Min-max normalization: Guarantees all features will have the
exact same scale but does not handle outliers well.
Z-score normalization: Handles outliers, but does not produce
normalized data with the exact same scale.

49. Time to apply what you’ve learnt!
___________

50. Before we get started
Go to kaggle.com and register for a
new account.

51. Before we get started
Now go to
bit.ly/gdsc-linear-reg-kaggle and
click on ‘Copy and Edit’ button
(top-right corner of the page).

52. Time to code!

53. Time to eat!

54. Logistic Regression
Learning to say “Yes” or “No”

55. Need for Logistic Regression
Why can’t we use Linear Regression and fit a
line??

56. Inaccurate Predictions

57. Out of Range Problem
For classification y=0 or y=1
In Linear Regression h(x) can be >1 or <0
But for Logistic Regression 0<= h(X) <= 1, must hold true

58. Hypothesis Representation
hθ
(x) = θT
X for linear regression.
But here we want 0<=hθ
(x)<=1

59. Sigmoid Function
hθ
(x) = g(θT
X), where g is the sigmoid function

60. Interpretation of hypothesis
hθ
(x) = Probability that y=1 given input x
For eg:
In cancer detection problem,
y = 1 signifies that a person has tested +ve for cancer
y = 0 signifies that a person has tested -ve for cancer
What does hθ
(x) = 0.7 mean for an example input x??

61. Decision Boundary
Predict y = 1 if hθ
(x)>=0.5 & y = 0 if hθ
(x)<0.5
Hence for y = 1:
⇒ hθ
(x)>=0.5
⇒ θT
X > 0

62. How does the model know when to
predict y =1 or y=0 ?

64. Say we find that θ1
= -3, θ2
= 1, θ3
= 1
Hence, on substitution :
Predict y=1 if -3+x1
+x2
> 0 , else predict y=0
hθ
(x) = 0 is called the decision boundary
i.e -3+x1
+x2
= 0 is the decision boundary

65. Loss Function
Recall from linear regression where we used this formula for
calculating the loss of our model
It turns out, although this same method gives a metric for loss of the
model, it has a lot of local minima

66. Loss function
Let’s consider the graph for -log(x) and -log(1-x)
Engineering a better loss function

67. -log(x)
-log(1 -x)

68. Let’s consider the case for a
data-point, who’s y = 1
If our model predicts
a 0, ie H(x) = 0 (the
wrong answer), we
get a really high loss
But if our model predicts a 1, ie
H(x) = 1 (the right answer), we
get a low loss
y = - log(x)

69. Now let’s consider the case for
a data-point, who’s y = 0
If our model predicts
a 1, ie H(x) = 1 (the
wrong answer), we
get a really high loss
But if our model
predicts a 0, ie H(x) =
0 (the right answer),
we get a low loss
y = - log(1-x)

70. Loss Function
Cool math trick!

71. Time to code again!
___________

72. Head over to bit.ly/gdsc-logistic-reg-kaggle and
click on ‘Copy and Edit’
Don’t forget to sign in!

73. K-Means Clustering
Finding Clusters in Data

74. K-means Clustering : Theory
K-Means Clustering is an Unsupervised Machine
Learning algorithm. Here, the algorithm can identify
the similarities and differences in the data and divide
the data into several groups called clusters. K is the
number of clusters. We can determine that K value
according to the dataset.

75. K means Clustering : Algorithm
Step 1 : Choose the number of clusters (K value) according to the dataset.
K = 2 here.

76. K means Clustering : Algorithm
Step 2 : Select the centroid points at random K points

77. Step 3 : Assign each data point to the closest centroid. That forms K clusters.
K mean Clustering : Algorithm

78. K means Clustering : Algorithm
Euclidean Distance : If (x1
, y1
) and (x2
, y2
) are two points, then the
distance between them is given by

79. Step 4 : Compute and place the new centroid of each cluster
K means Clustering : Algorithm

80. Step 5 : Reassign each data point to the new closest centroid. This step
repeats till no reassignment takes place
K means Clustering : Algorithm

81. K means Clustering : Algorithm
Step 6 : Model is ready

82. K means Clustering :
Choosing the correct number of clusters

83. K means Clustering :
Elbow Method

84. Quick Recap!

85. Machine Learning
Roadmap!

86. We want to know how we did!
Please fill out the feedback form given below:
https://bit.ly/gdsc-ml-feedback
Registered participants who’ve filled the form will
be eligible for certificates.

87. We want to know how we did!
We request all of you to check your inbox from
email from GDSC Event Platform. You will get it
soon.
Registered participants who’ve filled the form will
be eligible for certificates.

89. RESOURCES!
bit.ly/gdsc-explore-ml

90. Thank You!