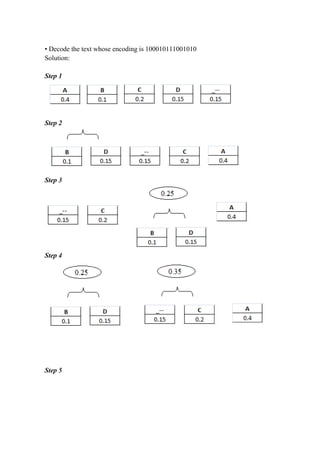
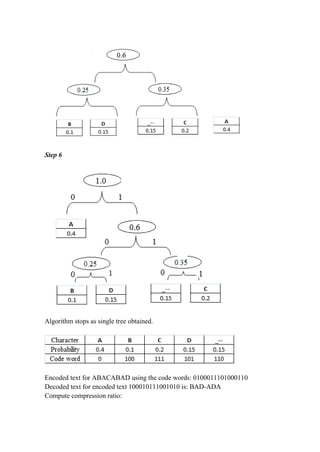
The document discusses greedy algorithms and matroids. It provides examples of problems that can be solved using greedy approaches, including sorting an array, the coin change problem, and activity selection. It defines key aspects of greedy algorithms like the greedy choice property and optimal substructure. Huffman coding is presented as an application that constructs optimal prefix codes. Finally, it introduces matroids as an abstract structure related to problems solvable by greedy methods.

1. 1.4.1. Introduction
Let we are given a problem to sort the array a = {5, 3, 2, 9}. Someone
says the array after sorting is {1, 3, 5, 7}. Can we consider the answer is
correct? The answer is definitely “no” because the elements of the output set are
not taken from the input set. Let someone says the array after sorting is {2, 5, 3,
9}. Can we admit the answer? The answer is again “no” because the output is
not satisfying the objective function that is the first element must be less than
the second, the second element must be less than the third and so on. Therefore,
the solution is said to be a feasible solution if it satisfies the following
constraints.
(i)Explicit constraints: - The elements of the output set must be taken from the
input set.
(ii)Implicit constraints:-The objective function defined in the problem.
The best of all possible solutions is called the optimal solution. In other
words we need to find the solution which has the optimal (maximum or
minimum) value satisfying the given constraints.
The Greedy approach constructs the solution through a sequence of steps.
Each step is chosen such that it is the best alternative among all feasible choices
that are available. The choice of a step once made cannot be changed in
subsequent steps.
Let us consider the problem of coin change. Suppose a greedy person has
some 25p, 20p, 10p, 5paise coins. When someone asks him for some change
then be wants to given the change with minimum number of coins. Now, let
someone requests for a change of top then he first selects 25p. Then the
remaining amount is 45p. Next, he selects the largest coin that is less than or
equal to 45p i.e. 25p. The remaining 20p is paid by selecting a 20p coin. So the
demand for top is paid by giving total 3 numbers of coins. This solution is an
optimal solution. Now, let someone requests for a change of 40p then the
Greedy approach first selects 25p coin, then a 10p coin and finally a 5p coin.
However, the some could be paid with two 20p coins. So it is clear from this

2. example that Greedy approach tries to find the optimal solution by selecting the
elements one by one that are locally optimal. But Greedy method never gives
the guarantee to find the optimal solution.
The choice of each step is a greedy approach is done based in the following:
 It must be feasible – it should satisfy the problems constraints
 It must be locally optimal –among all feasible solutions the best choice
is to be made.
 It must be unalterable – once the particular choice is made then it should
not get changed on subsequent steps
Greedy algorithm
//in Greedy approach D is a domain
//from which solution is to be obtained of size n
//Initially assume
Solution  0
for i  1 to n do {
S  select(D) //selection of solution from D
If(feasible (solution, s)) then
Solution  union(solution,s)
}
Return solution
In greedy method following activities are performed.
1. First we select some solution form input domain
2. Then we check whether the solution is feasible or not
3. Form the set of feasible solutions, particular solution that satisfies or nearly
satisfies the objective of the function. Such a solution is called optimal
solution.
4. As greedy method works in stages. At each stage only input is considered at
each time. Based on this input it is decided whether particular input given
the optimal solution or not
1.4.2. An activity selection problem
The activity selection problem is a mathematical optimization problem.
That concerning the selection of non-conflicting activities. Each activity assigned
by a start time (si) and finish time (fi). The activity selection problem is to select the
maximum number of activities that can be performed by a single machine, assuming
that a machine can only work on a single activity at a time.

3. Greedy Activity Selector Algorithm
Greedy-Activity-Selector(s, f)
1. n ← length[s]
2. A ← {a1}
3. i ← 1
4. for m ← 2 to n
5. do if sm ≥ fi
6. then A ← A U {am}
7. i ← m
8. return A
Example
Points to remember
 For this algorithm we have a list of activities with their starting time
and finishing time.
 Our goal is to select maximum number of non-conflicting activities that
can be performed by a person or a machine, assuming that the person or
machine involved can work on a single activity at a time.
 Any two activities are said to be non-conflicting if starting time of one
activity is greater than or equal to the finishing time of the other
activity.
 In order to solve this problem we first sort the activities as per their
finishing time in ascending order.
 Then we select non-conflicting activities.
Problem
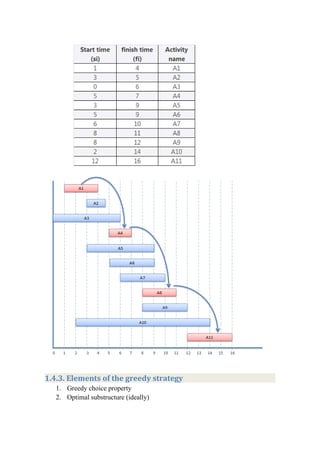
Consider the following 8 activities with their starting and finishing time.
Our goal is to find non-conflicting activities.
For this we follow the given steps
1. sort the activities as per finishing time in ascending order
2. select the first activity
3. select the new activity if its starting time is greater than or equal to the
previously selected activity
REPEAT step 3 till all activities are checked
Step 1: sort the activities as per finishing time in ascending order
Step 2: select the first activity
Step 3: select next activity whose start time is greater thanor equal to the finish
time of the previously selected activity

4. 1.4.3. Elements of the greedy strategy
1. Greedy choice property
2. Optimal substructure (ideally)

5. Greedy choice property: Globally optimal solution can be arrived by making a
locally optimal solution (greedy). The greedy choice property is preferred since
then the greedy algorithm will lead to the optimal, but this is not always the
case – the greedy algorithm may lead to a suboptimal solution. Similar to
dynamic programming, but does not solve sub problems. Greedy strategy more
top-down, making one greedy choice after another without regard to
subsolutions.
Optimal substructure: Optimal solution to the problem contains within it
optimal solutions to sub problems. This implies we can solve sub problems and
build up the solutions to solve larger problems.
1.4.4. Huffman codes
The Huffman code uses a binary tree to describe the code. Each letter of
the alphabet is located at an external. The bit encoding is the path from the root to
the letter with moving to the left child generating a 0 and moving to right child
generating a 1. If we are actually using the tree to encode the text then we would
need an additional locater structure. Normal one would make a lookup table and
use the tree only to construct/determine the code. The tree is a satisfactory structure
to decode.
Some useful definitions:
• Code word: Encoding a text that comprises n characters from some
alphabet by assigning to each of the text’s characters some sequence of bits.
This bits sequence is called code word
• Fixed length encoding: Assigns to each character a bit string of the same
length.
• Variable length encoding: Assigns code words of different lengths to
different characters.
Problem:
How can we tell how many bits of an encoded text represent ith
character?
We can use prefix free codes
Prefix free code: In Prefix free code, no codeword is a prefix of a codeword of
another character.
Binary prefix code:
 The characters are associated with the leaves of a binary tree.
 All left edges are labeled 0
 All right edges are labeled 1

6.  Codeword of a character is obtained by recording the labels on the simple
path from the root to the character’s leaf.
 Since, there is no simple path to a leaf that continues to another leaf, no
codeword can be a prefix of another codeword
Algorithm Huffman(X)
//input: String X of length n with d distinct characters
//output: coding tree for X
Compute the frequency function f.
Initialize empty priority queue Q of trees
for each character c in X do
Create a single-node binary tree T storing c.
Insert T into Q with key f(c)
while Q.size() > 1 do
f1 = Q.minKey()
T1 = Q.removeMin()
f2 = Q.minKey()
T2 = Q.removeMin()
Create new binary tree T with left subtree T1 and right subtree T2
Insert T into Q with key f1 + f2
return tree Q. removeMin()
Construction:
Step 1: Initialize n one-node trees and label them with the characters of the
alphabet. Record the frequency of each character in its tree’s root to indicate the
tree’s weight. (More generally the weight of a tree will be equal to the sum of the
frequencies in the tree’s leaves)
Step 2: Repeat the following operation until a single tree is obtained. “Find two
trees with smallest weight. Make them the left and right sub-tree of a new tree and
record the sum of their weights in the root of the new tree as its weight”
Example:
Construct a Huffman code for the following data:
• Encode the text ABACABAD using the code.

7. • Decode the text whose encoding is 100010111001010
Solution:
Step 1
Step 2
Step 3
Step 4
Step 5

8. Step 6
Algorithm stops as single tree obtained.
Encoded text for ABACABAD using the code words: 0100011101000110
Decoded text for encoded text 100010111001010 is: BAD-ADA
Compute compression ratio:

9. Bits per character = Codeword length * Frequency
= ( 1 * 0.4 ) + ( 3 * 0.1) + ( 3 * 0.2 ) + ( 3 * 0.15 ) + ( 3 * 0.15 )
= 2.20
Compression ratio is = ( 3 – 2.20 )/ 3 . 100% = 26.6%
1.4.5. Matroids and Greedy Methods
Many problems that can be correctly solved by greedy algorithms can be
described in terms of an abstract combinatorial object called a matroid. Matroids
were first described in 1935 by the mathematician Hassler Whitney as a
combinatorial generalization of linear independence of vectors—‘matroid’ means
‘something sort of like a matrix’.
A matroid M is a finite collection of finite sets that satisfies three axioms:
 Non-emptiness: The empty set is in M. (Thus, M is not itself empty.)
 Heredity: If a set X is an element of M, then every subset of X is also in M.
 Exchange: If X and Y are two sets in M where | X | > |Y |, then there is an
element x € X Y such that Y U {x} is in M.
The sets in M are typically called independent sets;
for example, we would say that any subset of an independent set is
independent. The union of all sets in M is called the ground set. An independent set
is called a basis if it is not a proper subset of another independent set. The exchange
property implies that every basis of a matroid has the same cardinality. The rank of
a subset X of the ground set is the size of the largest independent subset of X . A
subset of the ground set that is not in M is called dependent (surprise, surprise).
Finally, a dependent set is called a circuit if every proper subset is independent.
Most of this terminology is justified by Whitney’s original example:
Linear matroid: Let A be any n m matrix. A subset I {1, 2, . . . , n} is
independent if and only if the corresponding subset of columns of A is linearly
independent.
The heredity property follows directly from the definition of linear
independence; the exchange property is implied by an easy dimensionality
argument. A basis in any linear matroid is also a basis (in the linear-algebra sense)
of the vector space spanned by the columns of A. Similarly, the rank of a set of
indices is precisely the rank (in the linear-algebra sense) of the corresponding set of
column vectors.

10. Uniform matroid Uk,n : A subset X f1, 2, . . . , ng is independent if and only if |
X| ≤ k. Any subset of {1, 2, . . . , n} of size k is a basis; any subset of size k + 1 is a
circuit.
Graphic/cycle matroid M(G): Let G = (V, E) be an arbitrary undirected graph. A
subset of E is independent if it defines an acyclic subgraph of G. A basis in the
graphic matroid is a spanning tree of G; a circuit in this matroid is a cycle in G.
Cographic/cocycle matroid M (G): Let G = (V, E) be an arbitrary undirected
graph. A subset I E is independent if the complementary subgraph (V, E I) of G is
connected. A basis in this matroid is the complement of a spanning tree; a circuit in
this matroid is a cocycle—a minimal set of edges that disconnects the graph.
Matching matroid: Let G = (V, E) be an arbitrary undirected graph. A subset
I V is independent if there is a matching in G that covers I.
Disjoint path matroid: Let G = (V, E) be an arbitrary directed graph, and let s be a
fixed vertex of G. A subset I V is independent if and only if there are edge-disjoint
paths from s to each vertex in I.
Now suppose each element of the ground set of a matroid M is given an
arbitrary non-negative weight. The matroid optimization problem is to compute a
basis with maximum total weight. For example, if M is the cycle matroid for a
graph G, the matroid optimization problem asks us to find the maximum spanning
tree of G. Similarly, if M is the cocycle matroid for G, the matroid optimization
problem seeks (the complement of) the minimum spanning tree.
The following natural greedy strategy computes a basis for any weighted matroid:

11. Suppose we can test in F (n) whether a given subset of the ground set is
independent. Then this algorithm runs in O(n log n + n F (n)) time.
Theorem. For any matroid M and any weight function w, GreedyBasis(M, w)
returns a maximum-weight basis of M.
Proof: We use a standard exchange argument. Let G = {g1, g2, . . . , gk} be the
independent set returned by GreedyBasis(M, w). If any other element could be
added to G to obtain a larger independent set, the greedy algorithm would have
added it. Thus, G is a basis.
For purposes of deriving a contradiction, suppose there is an independent set H =
{h1, h2, . . . , hl} such that
Without loss of generality, we assume that H is a basis. The exchange property now
implies that k = l.
Now suppose the elements of G and H are indexed in order of decreasing weight.
Let i be the smallest index such that w(gi ) < w(hi ), and consider the independent
sets
Gi-1 = {g1, g2, . . . , gi-1} and Hi = {h1, h2, . . . , hi -1, hi }.
By the exchange property, there is some element hj ∈ Hi such that Gi-1 {hj} is an
independent set. We have w(hj ) ≥ w(hi ) > w(gi ). Thus, the greedy algorithm
considers and rejects the heavier element hj before it considers the lighter element gi
. But this is impossible—the greedy algorithm accepts elements in decreasing order
of weight. ƒ
We now immediately have a correct greedy optimization algorithm for any
matroid. Returning to our examples:
Linear matroid: Given a matrix A, compute a subset of vectors of maximum total
weight that span the column space of A.
Uniform matroid: Given a set of weighted objects, compute its k largest elements.
Cycle matroid: Given a graph with weighted edges, compute its maximum spanning
tree. In this setting, the greedy algorithm is better known as Kruskal’s algorithm.

12. Cocycle matroid: Given a graph with weighted edges, compute its minimum
spanning tree.
Matching matroid: Given a graph, determine whether it has a perfect matching.
Disjoint path matroid: Given a directed graph with a special vertex s, find the
largest set of edge-disjoint paths from s to other vertices.
The exchange condition for matroids turns out to be crucial for the success of this
algorithm. A subset system is a finite collection S of finite sets that satisfies the
heredity condition—If X ∈ S and YX , then Y ∈ S—but not necessarily the
exchange condition.
1.4.6. Unit time Task Scheduling
Independence