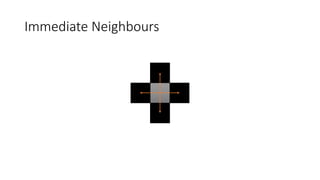
This document presents an algorithm for solving maze problems using backtracking. It first defines a maze as a confusing network of paths and hedges designed as a puzzle. It then explains that mazes can be solved by computers by devising an algorithm for a given maze. Specifically, it proposes using a backtracking approach due to the predefined constraints of mazes. The document provides pseudocode for a recursive backtracking algorithm that uses a depth-first search to find a clear path from the starting to ending position in a maze, represented as a 2D array. It analyzes the time complexity of this algorithm and suggests ways to potentially improve it.

1. “MAZE” Problem
& its Solution
By-Mudit Dholakia(14MTPOS001-MT005)
Guide:-Prof.P.M.Jadav

2. What is ‘maze’?
• Maze means confusing in nature.
• A network of paths and hedges designed as a puzzle through which
one has to find a way.
• DAZED

3. What to do with computers?
• It is easy to understand for a matured person.
• But what if we solve it using computer.????
?

4. Instruct Computer
• Solution is to devise an algorithm for given maze.
DYNAMIC
EFFECTIVE

5. Available Approaches
• Dynamic Programming
• Backtracking
• Greedy Approach

6. Backtracking?!
• We will solve this problem using backtracking.
• The reason behind this is we have pre-defined constraints.
• Hence it facilitates some ease for the programmer to choose the best
solutions.
• It also avoids undesired computations.

7. Example

8. Expected Solution
• 11x22 matrix
• “0”->wall
• “1”->gap
• Source Position (8,15)
• Destination Position(10,18)

9. Thinking from programmer’s perspective
• Constraints are there
• Array (matrix) is there
• Exploration of the right path is to be done
• “IN GENERAL WE HAVE TO FIND A CLEAR PATH TOWARDS
DESTINATION”
• 1. Consider the VISITED node, if it is ‘eligible’ for exploration.
• 2.Move forward else ‘stop’.

10. Ideal Algorithm
• 1. Consider a diamond neighbourhood of the algorithm.(i.e.
immediate neighbours HORIZONTALY and VERTICALY)
• 2.If ‘eligible’ move ahead having a track of backward knowledge
• 3.Else if not end then find another neighbour and follow step 2.
• 4.else ‘stop’

11. Tree consideration
• If we consider this problem solution to be an application of the
traditional tree then it is clear that “DFS-Depth First Search” tree
algorithm can solve this.
• Because in DFS we maintain all the visited track globally and move
further. So that visit consistency and order can be preserved.

12. Check for safe position
• int isSafe(int x,int y,int G[V1][V2],int Sol[V1][V2]) /* to check the safe move */
• {
• if(x>=0 && x<V1 && y>=0&&y<V2 && G[x][y]==1 && !Sol[x][y])
• {
• return 1;
• }
• else
• {
• return 0;
• }
• }

13. int MazeRecur(int G[V1][V2], int Sol[V1][V2], int x,int y) /* checking for the path to our exit point */
{
if(x==er &&y==ec)
{
Sol[x][y]=1;
return 1;
}
if(isSafe(x,y,G,Sol)==1)
{
printf("->(%d,%d)->",x,y);
Sol[x][y]=1;
if(MazeRecur(G,Sol,x,y-1)==1) /* left move possible */
{
return 1;
}
if(MazeRecur(G,Sol,x,y+1)==1) /* right move possible */
{
return 1;
}
if(MazeRecur(G,Sol,x-1,y)==1) /* up move possible */
{
return 1;
}
if(MazeRecur(G,Sol,x+1,y)==1) /* down move possible */
{
return 1;
}
Sol[x][y]=0;
}
return 0;
}

14. Immediate Neighbours

15. Implementing through C language

16. Time Complexity
• Consider only depth first search
of nodes.
• For mxn matrix to iterate the
search of node it will take
T(n*m/2) in worst case.
• And we add DFS recursive
backtrack algorithm time
T(n)=4T(n-1) for the 4 immediate
neighbours.
• T(n)=4T(nxm)
• Using master’s theorem it will
take 4 𝑛∗𝑚 exponential time.
• If we use backtracking then it
can be reduced to 2 𝑛∗𝑚
.

17. Improved algorithm can be designed …
• Using stack
• Using some enumerated datatypes
• Using K-connected neighbourhood concept
• Indexed data structures

18. References
• http://www.geeksforgeeks.org/backttracking-set-2-rat-in-a-maze/
• http://en.wikipedia.org/wiki/Maze_solving_algorithm
• https://www.cs.bu.edu/teaching/alg/maze/
• http://techlanguageworld.blogspot.in/2014/02/c-program-to-solve-
maze-problem.html

19. Queries?

20. THANK YOU