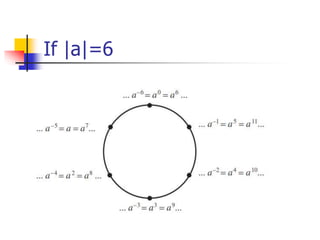
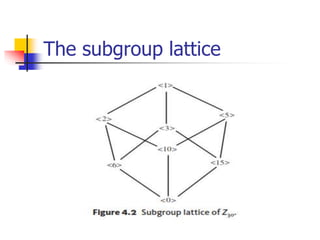
This document discusses properties of cyclic groups and subgroups of cyclic groups. It provides examples and proofs of theorems regarding cyclic groups. Specifically, it states that a subgroup of a cyclic group is cyclic, the order of any subgroup of a cyclic group must divide the order of the group, and for each positive integer k dividing the group order n, the group has exactly one subgroup of order k. It also provides examples of finding the order of elements in cyclic groups and calculating the Euler phi function for various numbers.

1. Chapter 4: Cyclic Groups
 Properties of Cyclic Groups
 Classification of Subgroups of Cyclic Groups

3. More Examples

4. More Examples
Therefore, U(8) is not cyclic.

6. Proof: continue

7. Proof: continue

9. If |a|=6

11. Proof; continue

12. Example:

19.  A subgroup of a cyclic group is cyclic.
 If |<a>|=n, then the order of any subgroup
of <a> divides n.
 For each +ve integer k, where
k divides n, the group <a> has exactly one
subgroup of order k, namely,

 k
n
a

20. Understanding the theorem

21. Proof: theorem 4.3

25. Example

29.  Euler phi function

31. Example
 Find the number of elements of order 8
in the cyclic group .
and
,
Z
, 320
8
8000000 Z
Z

33. Example: find the euler function value for each of the
following numbers: n=81, n=100
)
(
find
to
How n

)
(
)
(
)
(
then
prime,
relatively
are
n
m,
If
)
(
,
number
prime
any
For
1
n
m
mn
p
p
p
p
n
n
n






 

34. The subgroup lattice