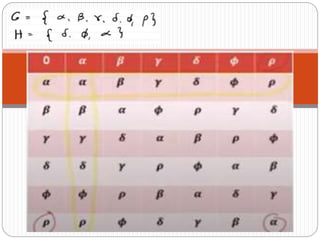
This document defines cosets and Lagrange's theorem. It defines a left coset as gH, the set of left multiplying an element g of a group G by elements of a subgroup H. A right coset is defined as Hg. Lagrange's theorem states that if H is a subgroup of a finite group G, the order of H divides the order of G. Examples are given of finding the left and right cosets of a subgroup H of the group Z12 and verifying they are equal, making H a normal subgroup. The order of a subgroup must divide the group order according to Lagrange's theorem.

1. COSETS AND LAGRANGE’S
THEOREM
JOHN MARIE M. NALAM
PRESENTERLAJJJJJGRANGE’S
THEOREM

2. Definition
Let G be a group and H a
subgroup G, let g be an element in G.
gH = {gh Ι h Є H} is called a left
coset of H in G.

3. The left coset is gH, but we can
similarly define the right coset of H in
G:
Hg = {hg I h Є H}

4. Definition
Let G be a group and H be a
subgroup. Then we say that H is a
normal subgroup of G if the sets of left
and right cosets of H and G coincide.

5. Examples:
1. Find the left and the right cosets of H = {0, 3, 6,
9} in 𝒁𝟏𝟐.
<3> = {3,6,9,0}
H = {0, 3, 6, 9} G = {1,2,3,4,5,6,7,8,9,10,11}
Right Cosets: Ha = {ha I h Є H, a Є G}
H0 = {0,3,6,9} = H H5 = {5,8,11,2} *
H1 = {1,4,7,10} *
H2 = {2,5,8,11} *
H3 = {3,6,9,0} = H
H4 = {4,7,10,1} *

6. H = {0, 3, 6, 9} G = {1,2,3,4,5,6,7,8,9,10,11}
Left Cosets: aH = {aH I, a Є G, h Є H}
0H = {0,3,6,9} = H
1H = {1,4,7,10}
2H = {2,5,8,11}
3H = {3,6,9,0} = H

7. Examples:
2. Find the left and the right cosets of
Are the left and the right cosets
equal?

9. Lagrange Theorem
Italian mathematician,
physicist and
astronomer.

10. Lagrange’s Theorem
If H ≤ G, then the order of H divides
the order of G.
Order of G = # of elements in G
= I G I
Lagrange’s Theorem:

11. Lagrange’s Theorem
If G is a finite group and H is a subgroup of G,
then I H I divides I G I
where I H I = order of H and I G I = order of G
or
The order of a Subgroup of a finite Group divides
the order of the Group.

12. Lagrange’s Theorem
Let G be a group with I G I = 323 = 17 x 19
Divisors of 323: 1, 17, 19, 323
Possible subgroups orders: 1, 17, 19, 323
Standard subgroups: G, {e}
I G I = 323
I{e}I = 1
Any other subgroup has order 17 or 19.

13. Example:
Find all possible Subgroups of the Group <G, *>. Where G = {1,-1,i,-i}
Sol:
Order of subgroup G is I G I = 4 (# of elements in G)
By Lagrange Theorem, order of each subgroup of G divides the order of G.
Divisors of order of G are 1, 2, 4 [Therefore 1 divides 4, 2 divides 4, 4 divides 4]
Hence, Subgroups of G order 1, 2, 4.
(i) Subgroup of order 1: H1 = {1} = e = 1
(ii) Subgroup of order 2: H2 = {1, -1}, H3 = {1, i}, H4 = (1, -i}
Therefore H2 is a subgroup but H3, H4 are not subgroup
(iii) Subgroup of order 4: H5 = {1, -1, i, -i}
Therefore H5 is a subgroup.

14. THANK YOU FOR
LISTENING…