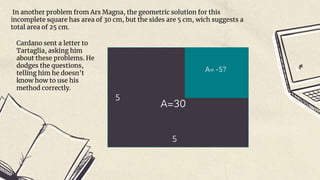
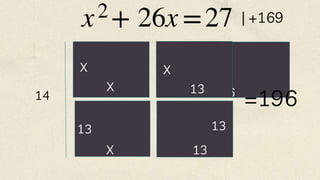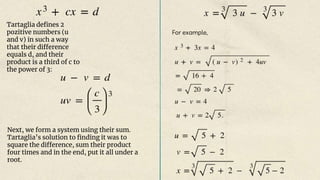The document outlines the historical development of complex numbers, focusing on key mathematicians such as Scipione del Ferro, Niccolò Fontana Tartaglia, Gerolamo Cardano, and Rafael Bombelli. It discusses their significant contributions to solving cubic equations and the eventual introduction of imaginary numbers. The project emphasizes the importance of these discoveries in the evolution of abstract mathematics and understanding the world.

1. The discovery
of complex
numbers
Group F+Fm1, First Year

2. Table of contents
01- The purpose of the project
02- Scipione del Ferro
03- Antonio Fior
05- Niccolo Fontana Tartaglia
06- Gerolamo Cardano
07- Rafael Bombelli
08- Conclusion

3. The purpose
of the project
01
The purpose of this project is to
answer the following questions:
❏ Who discovered complex numbers?
❏ When were they discovered?
❏ Why is this important?

4. The Quadratic equation

5. X
X
26
X
13
X
X
13
13
13
| +169
=196
14

7. That being said, a step above the
quadratic equation is the cubic equation:
This formula was belived to be impossible
to resolve, but in the 16th century, the
first steps were made in order to find the
answer. Everything began with Scipione
del Fero.

8. 02
Scipione del Fero
Born in Bologna, in the North of Italy, he
studied Mathematics at the University of
Bologna, where he became a professor in 1496.
Around the year 1510, he managed to
successfully resolve a simplified version of the
cubic equation (the depressed cubic):
∀ x,q,p>0

10. What did del Ferro do when he became the first person to solve this type of
equation?
Nothing.

11. And so, Ferro noted his discovery in a secret book, wich ended up in his
son in law’s possession, Annibale della Nave.
On his deathbed though, he told one of his students how to solve the
problem. His name?

12. 03
Antonio Fior
Antonio Fior wasn’t as good as his
mentor (or a very good mathematician in
general), but this detail didn’t stop him
from boasting about his ability to solve
the famous equation.
He challanges a newcomer in Venice,
his hometown.

13. 04
Niccolò Fontana “Tartaglia”
Niccolò Fontana was born in Brescia. In 1506
his father was murdered, leaving him,his
mother and his two brothers alone. Even
more then that, in 1512, France invaded
Brescia, where the soldiers left him with a
scar on his mouth and a speech impediment,
where his name Tartaglia comes from
(meaning “stutterer”).

14. Tartaglia defines 2
pozitive numbers (u
and v) in such a way
that their difference
equals d, and their
product is a third of c to
the power of 3:
Next, we form a system using their sum.
Tartaglia’s solution to finding it was to
square the difference, sum their product
four times and in the end, put it all under a
root.
For example,

15. In order to not go trough the geometric method every time (remember that they didn’t
have our notations) he wrote a poem:

16. With this victory also came the fame, but
Fontana refused to explain how he came
to his results, just like del Ferro. This is
where our next contestant comes in to
play.

17. 05
Gerolamo Cardano
A mathematician that had great
contributions to biology, chemistry and
physics. The difference between him
and the others however, was that he
didn’t work for other people, so he
wasn’t affected by the duel system.
He wrote numerous letters to Tartaglia,
ranging from complementing him to
insulting him, desperately trying to
learn how he managed to find the
solution.
His letters: https://mathshistory.st-
andrews.ac.uk/HistTopics/Tartaglia_v
_Cardan/

18. “ Written in five years, may it last for five hundred”

19. Cardano realised that if he replaced the “x” in this
way:
The result of this being a depressed cube,
something we already know how to solve.

20. That being said, Cardano discovered that some combinations of
numbers didn’t work for this method. For example:

21. In another problem from Ars Magna, the geometric solution for this
incomplete square has area of 30 cm, but the sides are 5 cm, wich suggests a
total area of 25 cm.
A=30
5
5
A= -5?
Cardano sent a letter to
Tartaglia, asking him
about these problems. He
dodges the questions,
telling him he doesn’t
know how to use his
method correctly.

22. 06
Rafael Bombelli
The author of the book “L’Algebra”, the engineer
and architect Rafael Bombelli, completed the
unsolved problems from Ars Magna, 10 years after
it’s debut, thus introducing for the first time the
concept of imaginary numbers.
Obviosly, they didn’t have that name yet.
Bombelli identifies (√-1) named piu di meno and (-
√-1) named meno di meno. This way, something
like 7+√-3 would have been read “ seven plus
three times plus of minus”.
Simmilarly, there is evidence that
suggest he developed a primitive
form of i^2=-2 and (i)*(-i)=1.

23. CREDITS:
This presentation template was created by
Slidesgo, including icons by Flaticon, infographics
& images by Freepik
07
Conclusion
The discovery of the method that solves the cubic equation, and trough it, the
eventual discovery of complex numbers, were humanity’s first steps towards
the understanding of abstract math, that helps us better understand how the
world works. Only when we stray away from nature we can truly begin to
describe it.

24. Sources
● Peters-Christen-HOM-SIGMAA-2018.pdf
● How Imaginary Numbers Were Invented- Veitasium
● Tartaglia V Cardano - Mac Tutor
● Wikipedia.org