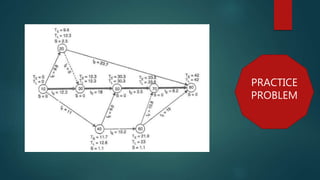
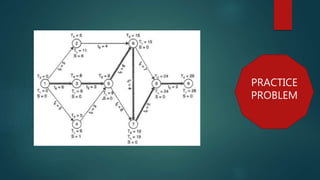
This document discusses construction project scheduling techniques including critical path method. It defines slack as the difference between earliest expected and latest allowable times, and explains that activities on the critical path with zero slack are most critical to completing the project on schedule. The document also provides steps to calculate the probability of meeting a scheduled completion date based on the critical path's standard deviation and the probability factor.

1. Construction Technology
and Management
Dr. Abhishek Jindal

2.  Slack
 Critical Path
 Practice Problem
 Probability of Meeting Scheduled date
Overview

3.  Earliest Expected time (TE)
 Latest Allowable Occurrence time (TL)
 Difference between latest allowable time and the earliest expected
time of an event - SLACK
S = TL - TE
 Slack gives idea of time to spare.
SLACK

4. SLACK

5. SLACK
Slack could be Positive, Negative or
Zero depending upon the relationship
between TE and TL.
Positive Slack - when TL is more than
TE for an event. Indicates Ahead of
Schedule condition.
Zero Slack - when TL is equal to TE for
for an event. Indicates On Schedule
condition.
Negative Slack - when TL is less than
TE for an event. Indicates Behind of
Schedule condition.

6. SLACK

7.  For an event - value of slack determines - how critical the event is.
 Less the slack time (even negative) - more critical an event is.
 A critical path is the one which connects the events having zero or
minimum slack times.
 Any delay in occurrence of events on critical path will result in the
delay in scheduled completion of project.
 Eventually, a critical path is the longest path (time wise) connecting the
initial and final event. CRITICAL
PATH

8. Determine the Critical Path for above network.
PRACTICE
PROBLEM

9.  Earliest expected time and Latest allowable occurrence time for each
event is already shown in network.
 Calculating Slack for each event by taking difference between Earliest
expected time and Latest allowable occurrence time for each event.
PRACTICE
PROBLEM

10. PRACTICE
PROBLEM

11. PRACTICE
PROBLEM
Determine the Critical Path for above network.

12. PRACTICE
PROBLEM

13. PRACTICE
PROBLEM

14. PRACTICE
PROBLEM
Determine the Critical Path for above network. Given
scheduled completion time is 21 days

15.  Latest Allowable Occurrence time - scheduled completion time
 Critical path
 What is the probability of meeting the scheduled time?
 Procedure for determining the probability of meeting the scheduled
time:
 Step 1: Determine standard deviation (σ) for critical path for network.
σ = (Sum of variances along critical path)1/2
σ = √ (Σ σ2)
Variance for an activity ij is given by
σ2
ij = (
tij
p − tijo
6
)2
 Step 2: Calculating Probability factor
Z =
𝑇𝑆
−𝑇𝐸
σ
=
𝑇𝑆 −𝑇𝐸
√ (Σ σ2)
PROBABILITY
OF MEETING
SCHEDULED
DATE

16.  Probability Factor (Z) can be positive, zero or negative.
 When Z is positive, chances of completing project on time are more than
50%.
 When Z is Zero, chances of completing project on time are fifty-fifty.
 When Z is negative, chances of completing project on time are less than
50%.
 Step 3: Find % Probability with respect to Z from table. PROBABILITY
OF MEETING
SCHEDULED
DATE

17. PROBABILITY
OF MEETING
SCHEDULED
DATE

18. PROBABILITY
OF MEETING
SCHEDULED
DATE

19. PROBABILITY
OF MEETING
SCHEDULED
DATE

20. PROBABILITY
OF MEETING
SCHEDULED
DATE

21. PROBABILITY
OF MEETING
SCHEDULED
DATE

22. PROBABILITY
OF MEETING
SCHEDULED
DATE

23. PROBABILITY
OF MEETING
SCHEDULED
DATE

24. END