Download to read offline
Resonance.pptx
- 1.
- 2. Series RLC CircuitParallel RLC Circuit RLC Circuit
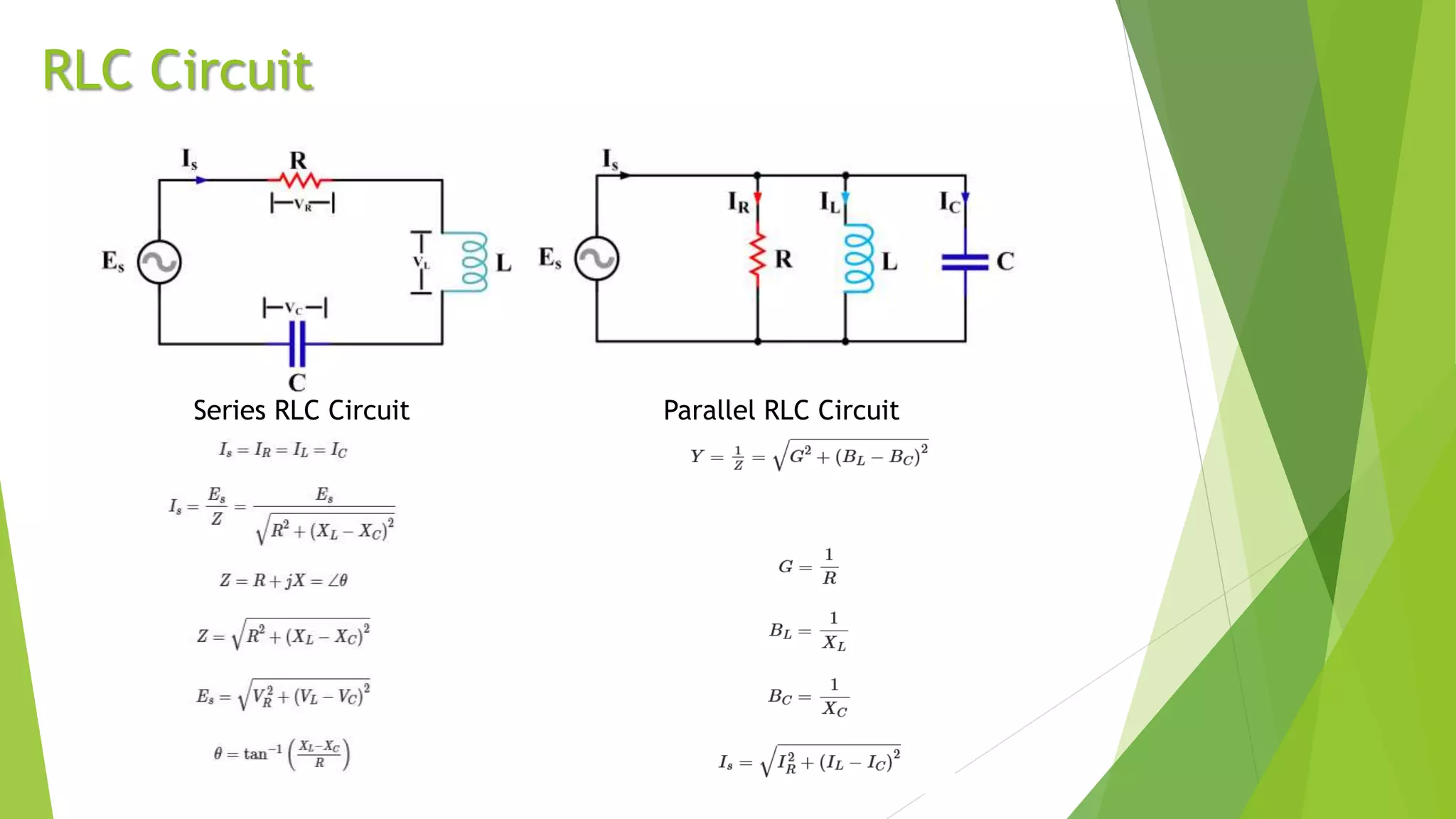
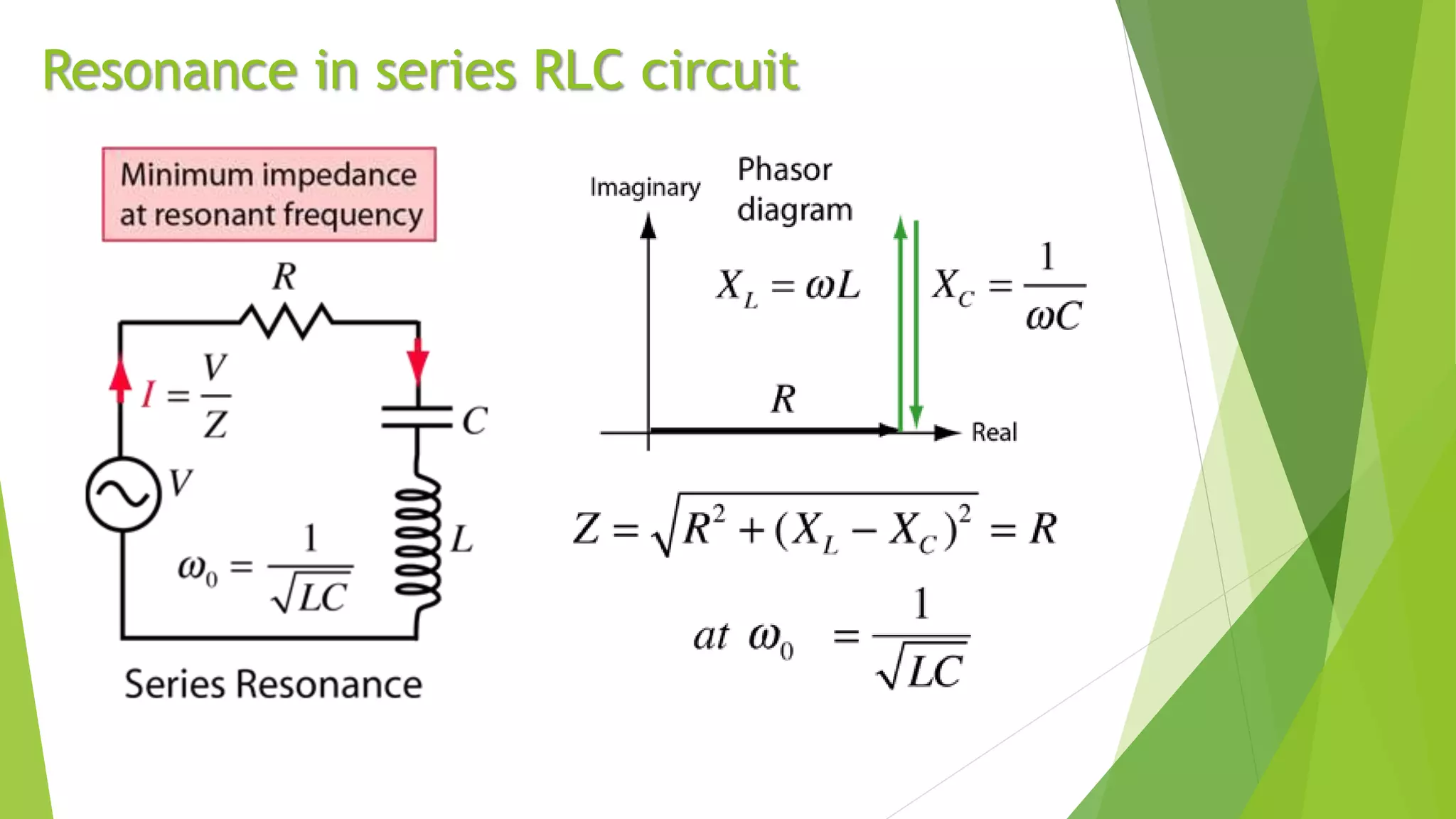
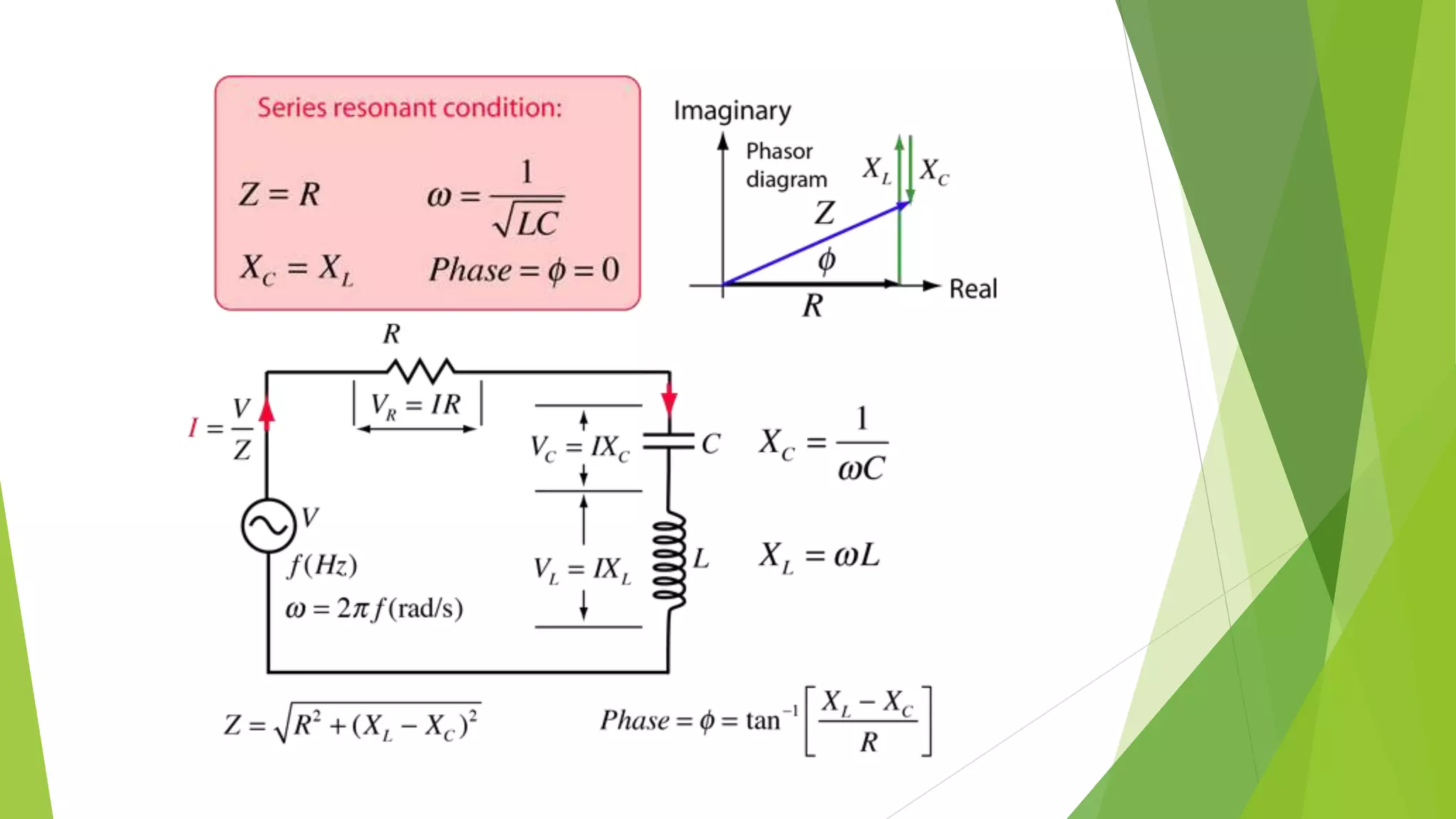
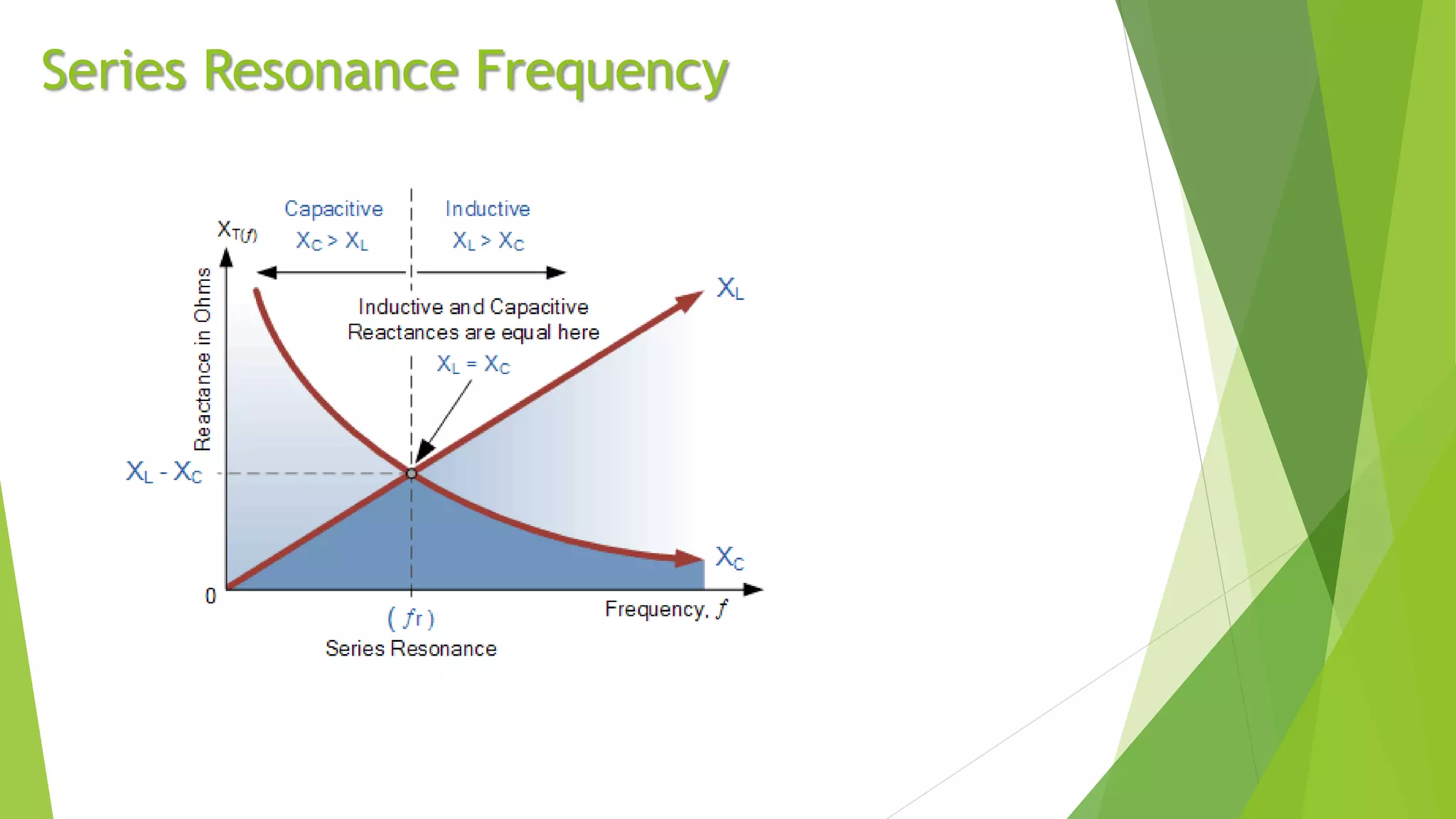
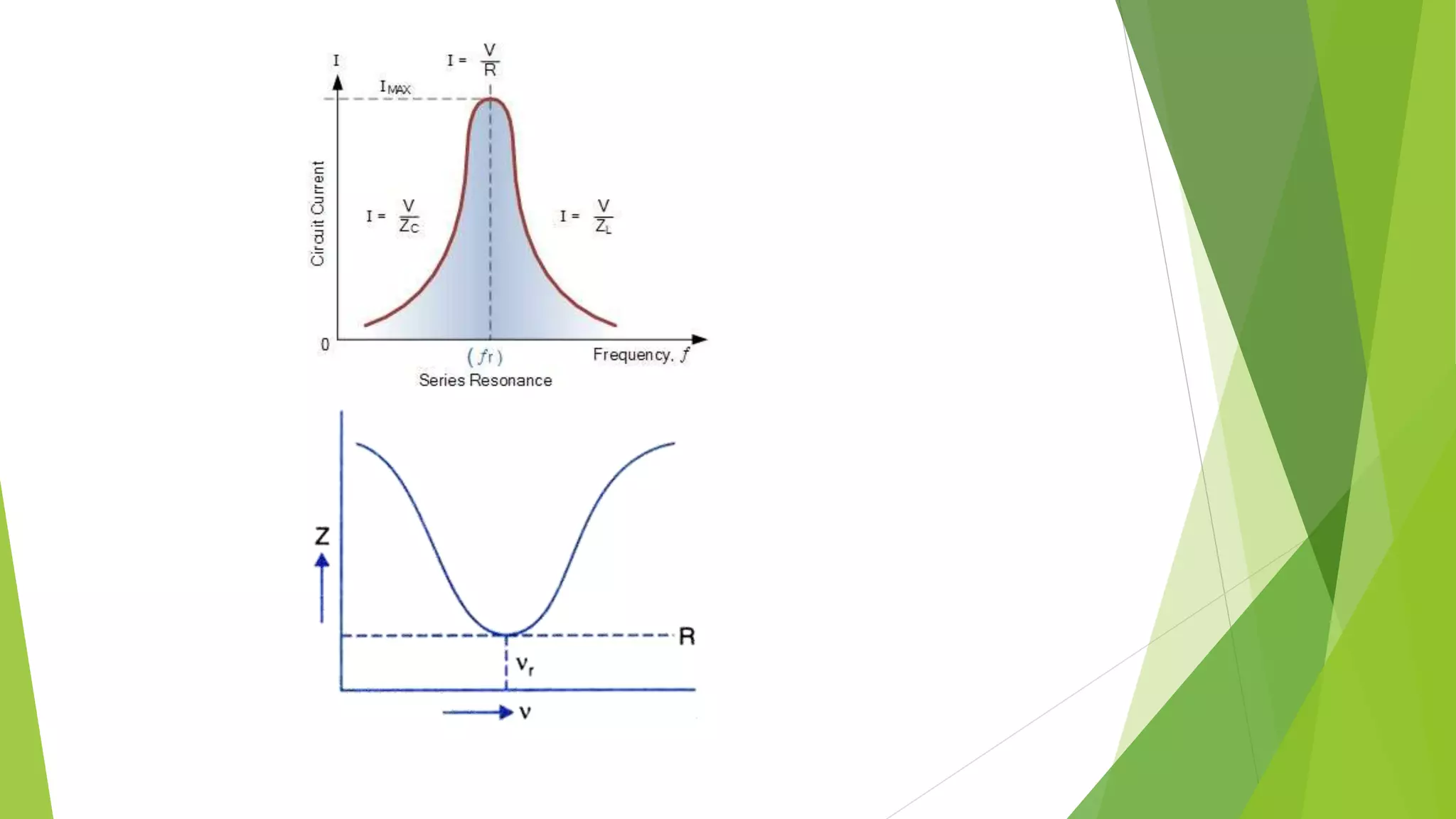
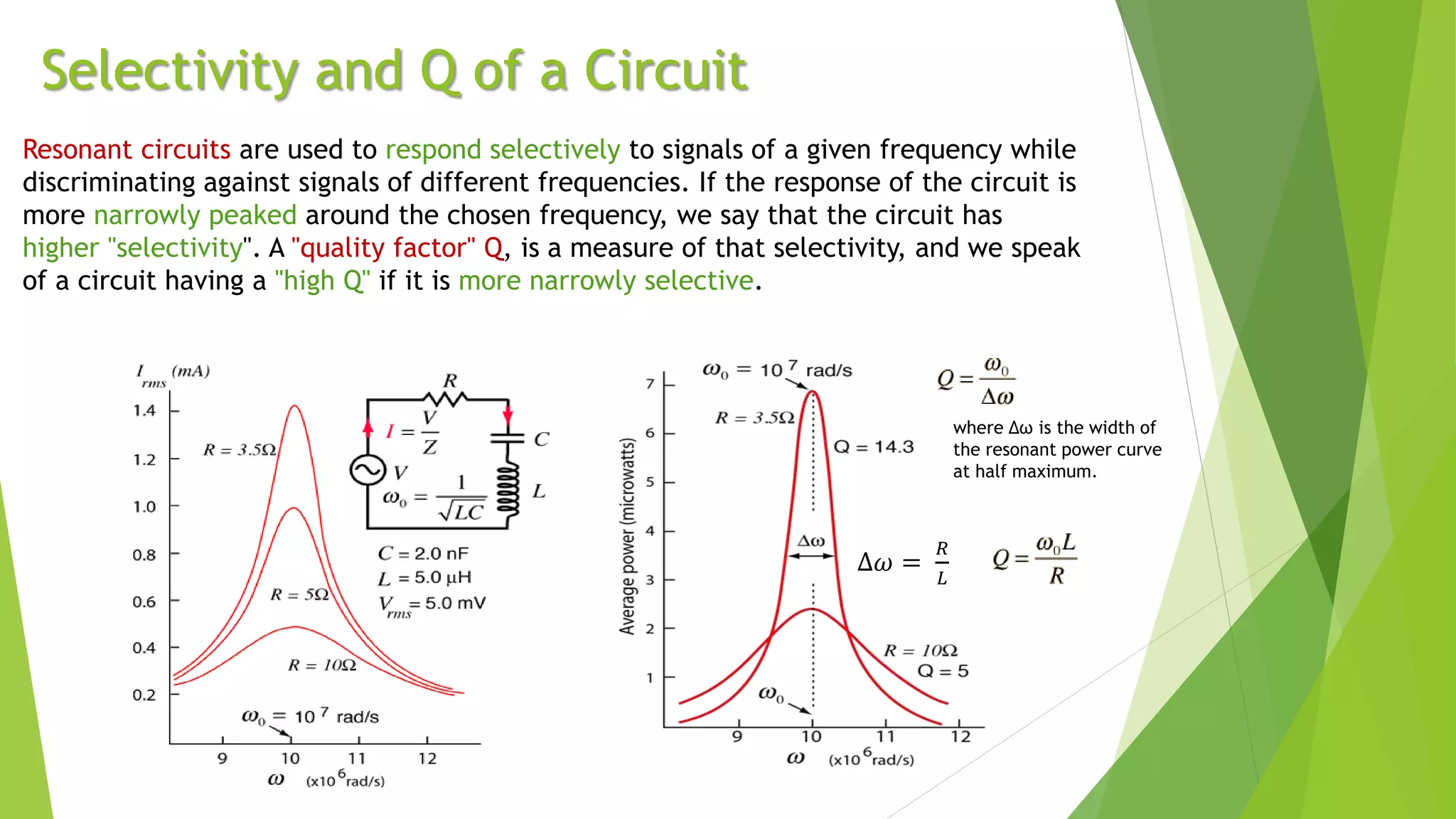
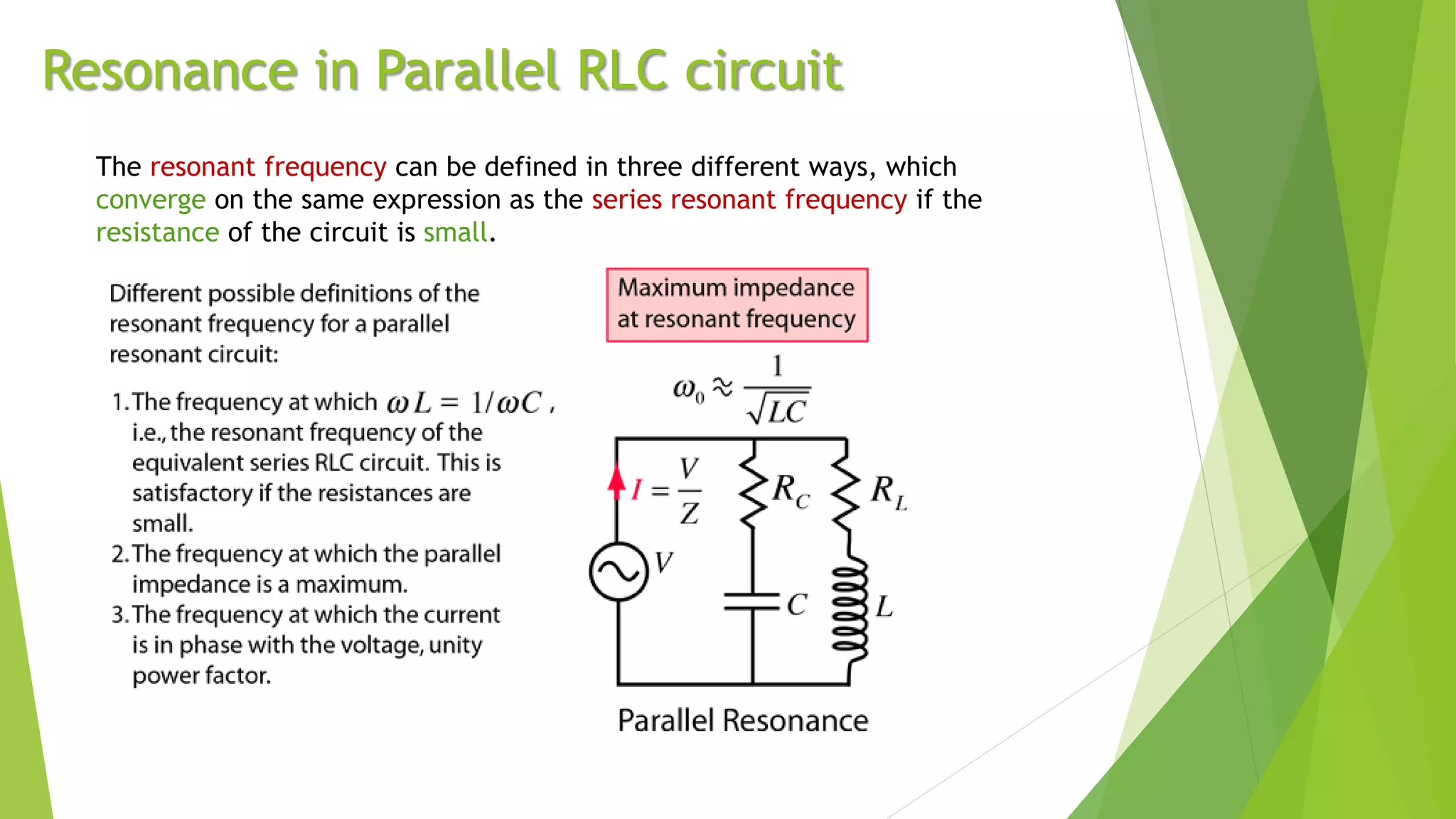
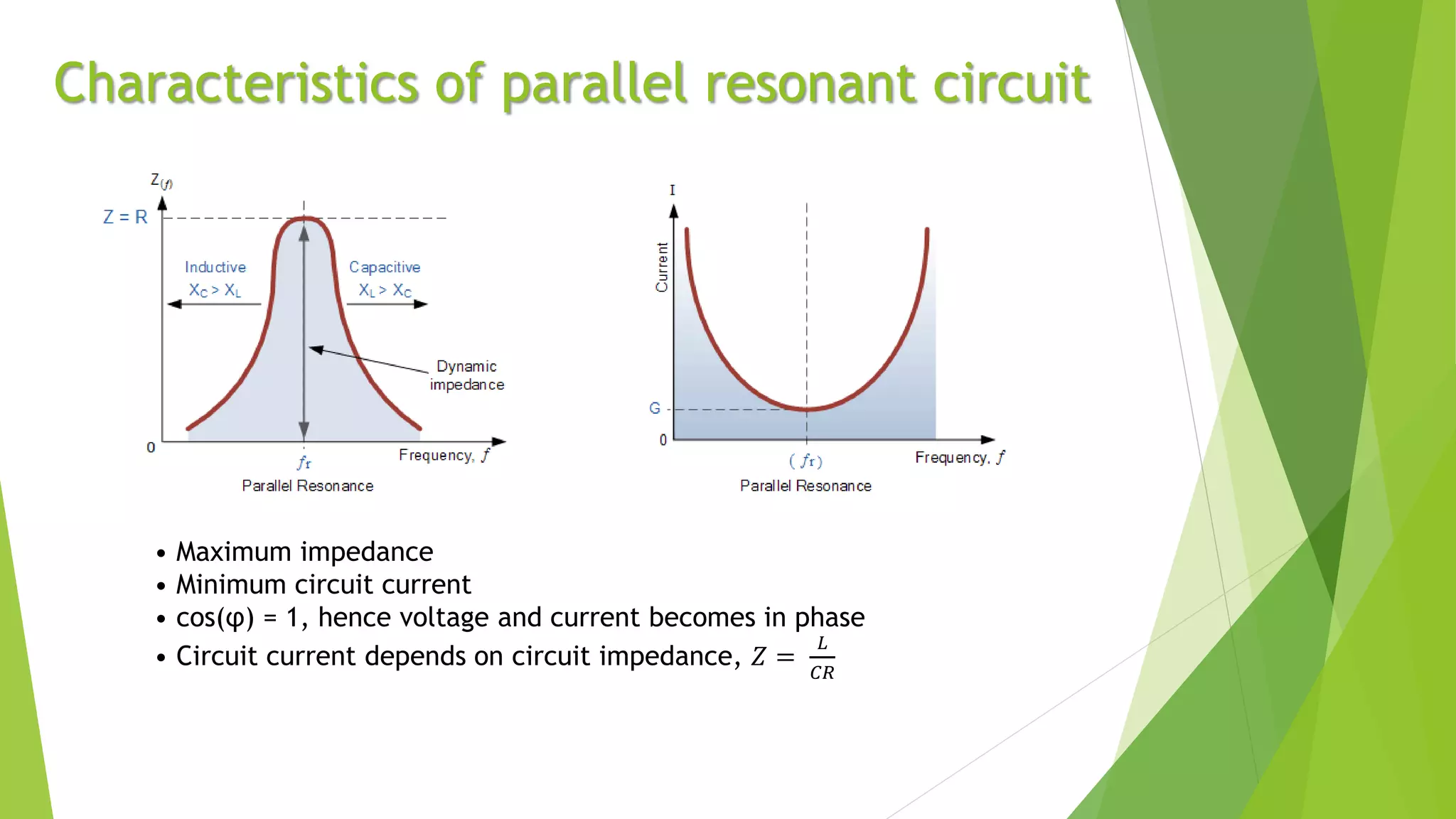
- 3. Resonance in anRLC Circuit is a special condition for parallel and series RLC circuits, when capacitive reactance and inductive reactance have the same magnitude and cancel each other. This only happens at some frequency named resonance frequency (f0). Electrical Resonance Resonant circuits can generate very high voltages. A tesla coil is a high-Q resonant circuit tuner of a television set
- 4. Resonance in seriesRLC circuit
- 6.
- 7. Characteristics of seriesresonant circuit XL = XC 𝑓𝑟 = 1 2𝜋 𝐿𝐶 The impedance is minimum and purely resistive. The current has a maximum value of 𝜀0 𝑅 at resonant condition. 𝐼0 = 𝜀0 𝑅2+ 𝜔𝐿 − 1 𝜔𝑐 2 , Clearly 𝐼0 becomes maximum when 𝜔 = 1 𝐿𝐶 The power dissipated in the circuit is maximum and is equal to 𝜀𝑟𝑚𝑠 2 𝑅 The Current is in phase with the voltage or the power factor is unity. cos 𝜙 = 1 , 𝑤ℎ𝑒𝑛 𝜙 = 0
- 9. Selectivity and Qof a Circuit Resonant circuits are used to respond selectively to signals of a given frequency while discriminating against signals of different frequencies. If the response of the circuit is more narrowly peaked around the chosen frequency, we say that the circuit has higher "selectivity". A "quality factor" Q, is a measure of that selectivity, and we speak of a circuit having a "high Q" if it is more narrowly selective. Δ𝜔 = 𝑅 𝐿 where Δω is the width of the resonant power curve at half maximum.
- 10. Expression for QualityFactor - Q
- 11. Tuning of aRadio Receiver An example of the application of resonant circuits is the selection of AM radio stations by the radio receiver. The selectivity of the tuning must be high enough to discriminate strongly against stations above and below in carrier frequency, but not so high as to discriminate against the "sidebands" created by the imposition of the signal by amplitude modulation. The selectivity of a circuit is dependent upon the amount of resistance in the circuit. The smaller the resistance, the higher the "Q" for given values of L and C.
- 12. Resonance in ParallelRLC circuit The resonant frequency can be defined in three different ways, which converge on the same expression as the series resonant frequency if the resistance of the circuit is small.
- 13. Parallel RLC circuit– Resonate frequency Finding the impedance of a parallel RLC circuit is considerably more difficult than finding the series RLC impedance. This is because each branch has a phase angle and they cannot be combined in a simple way. The impedance of the parallel branches combine in the same way that parallel resistors combine: But although the branch impedance magnitudes can be calculated from they cannot be directly combined as suggested by the expression above because they are different in phase - like vectors in different directions cannot be added directly. This dilemma is most easily solved by the complex impedance method. By setting the = 0, the resonant frequency can be calculated. Note that for small values of the resistances, this approaches the series resonant frequency
- 14. Characteristics of parallelresonant circuit • Maximum impedance • Minimum circuit current • cos(φ) = 1, hence voltage and current becomes in phase • Circuit current depends on circuit impedance, 𝑍 = 𝐿 𝐶𝑅
- 16. References Halliday Resnick,Jearl Walker 9th edition, International Student Version, Chapter 31 Electromagnetic Oscillations and Alternating current. New Simplified Physics by S.L. Arora hyperphysics.phy-astr.gsu.edu electronics-tutorials.ws rfwireless-world.com kullabs.com electrical4u.com theelectricalportal.com
Editor's Notes
- #4 Resonant circuits can generate very high voltages. A tesla coil is a high-Q resonant circuit tuner of a television set.