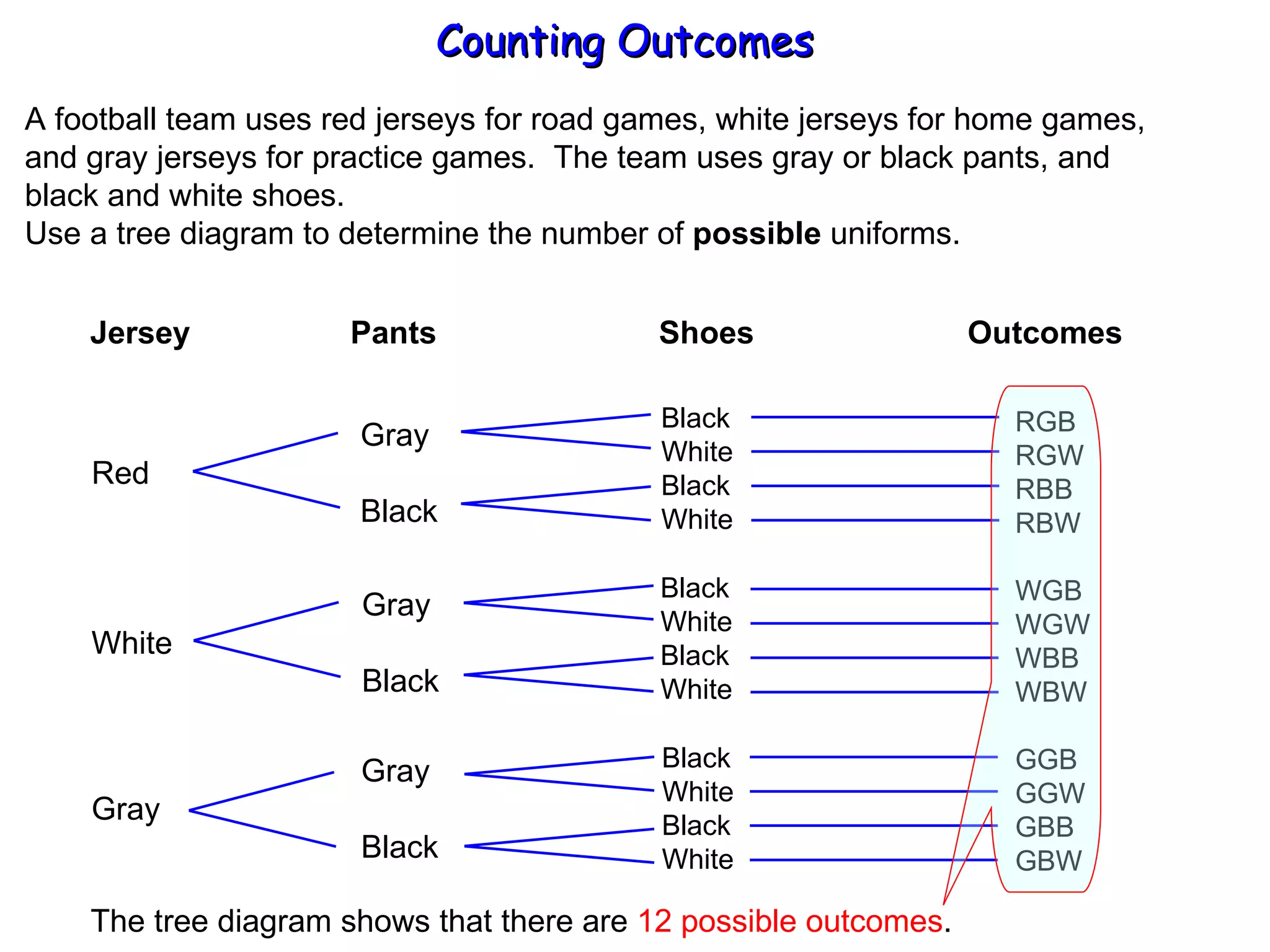
The document discusses different methods for counting outcomes and possibilities, including tree diagrams and the Fundamental Counting Principle. It provides examples of using each method to count the number of possible uniforms for a football team and possible lunch special combinations at a deli. It also explains that the number of arrangements of 10 video games can be found using the factorial formula 10!.

1. What You'll Learn Vocabulary 1) tree diagram 2) sample space 3) event 4) Fundamental Counting Principle 5) Factorial Counting Outcomes Count outcomes using a tree diagram. Count outcomes using the Fundamental Counting Principle.

2. Counting Outcomes One method used for counting the number of possible outcomes is to draw a tree diagram . The last column of a tree diagram shows all of the possible outcomes . The list of all possible outcomes is called the sample space , while any collection of one or more outcomes in the sample space is called an event .

3. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms.

4. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms. Jersey Pants Shoes Outcomes Red White Gray

5. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms. Jersey Pants Shoes Outcomes Red White Gray Gray Black Gray Black Gray Black

6. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms. Jersey Pants Shoes Outcomes Red White Gray Gray Black Gray Black Gray Black Black White Black White Black White Black White Black White Black White

7. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms. Jersey Pants Shoes Outcomes Red White Gray Gray Black Gray Black Gray Black Black White Black White RGB RGW RBB RBW WGB WGW WBB WBW GGB GGW GBB GBW Black White Black White Black White Black White

8. Counting Outcomes A football team uses red jerseys for road games, white jerseys for home games, and gray jerseys for practice games. The team uses gray or black pants, and black and white shoes. Use a tree diagram to determine the number of possible uniforms. Jersey Pants Shoes Outcomes Red White Gray Gray Black Gray Black Gray Black Black White Black White RGB RGW RBB RBW WGB WGW WBB WBW GGB GGW GBB GBW Black White Black White Black White Black White The tree diagram shows that there are 12 possible outcomes .

9. Counting Outcomes In the previous example, the number of possible outcomes could also be found by multiplying the number of choices for each item.

10. Counting Outcomes In the previous example, the number of possible outcomes could also be found by multiplying the number of choices for each item. The team could choose from: 3 different colored jerseys 2 different colored pants 2 different colored shoes

11. Counting Outcomes In the previous example, the number of possible outcomes could also be found by multiplying the number of choices for each item. The team could choose from: 3 different colored jerseys 2 different colored pants 2 different colored shoes There are 3 X 2 X 2 or 12 possible uniforms.

12. Counting Outcomes In the previous example, the number of possible outcomes could also be found by multiplying the number of choices for each item. The team could choose from: 3 different colored jerseys 2 different colored pants 2 different colored shoes There are 3 X 2 X 2 or 12 possible uniforms. This example illustrates the Fundamental Counting Principle .

13. Counting Outcomes In the previous example, the number of possible outcomes could also be found by multiplying the number of choices for each item. The team could choose from: 3 different colored jerseys 2 different colored pants 2 different colored shoes There are 3 X 2 X 2 or 12 possible uniforms. This example illustrates the Fundamental Counting Principle . If an event M can occur in m ways, and is followed by an event N that can occur in n ways, then the event M followed by event N can occur m X n ways.

14. Counting Outcomes A deli offers a lunch special in which you can choose a sandwich, a side dish, an a beverage. If there are 10 different sandwiches, 12 different side dishes, and 7 different beverages, from which to choose, how many different lunch specials can be ordered?

15. Counting Outcomes A deli offers a lunch special in which you can choose a sandwich, a side dish, an a beverage. If there are 10 different sandwiches, 12 different side dishes, and 7 different beverages, from which to choose, how many different lunch specials can be ordered? Multiply to find the number of lunch specials. sandwich choices side dish choices beverage choices number of specials X X =

16. Counting Outcomes A deli offers a lunch special in which you can choose a sandwich, a side dish, an a beverage. If there are 10 different sandwiches, 12 different side dishes, and 7 different beverages, from which to choose, how many different lunch specials can be ordered? Multiply to find the number of lunch specials. 10 X 12 X 7 = 840 The number of different lunch specials is 840 . sandwich choices side dish choices beverage choices number of specials X X =

17. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them?

18. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position.

19. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position.

20. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position. After choosing a game for the first position, there are nine games left from which to choose for the second position.

21. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position. After choosing a game for the first position, there are nine games left from which to choose for the second position. There are now eight choices for the third position.

22. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position. After choosing a game for the first position, there are nine games left from which to choose for the second position. There are now eight choices for the third position. This process continues until there is only one choice left for the last position.

23. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position. After choosing a game for the first position, there are nine games left from which to choose for the second position. There are now eight choices for the third position. This process continues until there is only one choice left for the last position. Let n represent the number of arrangements. n = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 or 3,628,800

24. Counting Outcomes A.J. is setting up a display of the ten most popular video games from the previous week. If he places the games side-by-side on a shelf, in how many different ways can he arrange them? The number of ways to arrange the games can be found by multiplying the number of choices for each position. A.J. has 10 games from which to choose for the first position. After choosing a game for the first position, there are nine games left from which to choose for the second position. There are now eight choices for the third position. This process continues until there is only one choice left for the last position. Let n represent the number of arrangements. n = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 or 3,628,800 There are 3,628,800 different ways to arrange the video games.

25. Counting Outcomes The expression n = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 used in the previous example can be written as 10! using a factorial . The expression n! , read n factorial, where n is greater than zero, is the product of all positive integers beginning with n and counting backward to 1. n! = n(n – 1)* (n – 2) * . . . 3 * 2 * 1 Example: 5! = 5 * 4 * 3 * 2 * 1 or 120

26. Counting Outcomes 0! is defined as being equal to 1. Let’s see why.

27. Counting Outcomes 0! is defined as being equal to 1. Let’s see why. Writing this out using the definition of factorials.

28. Counting Outcomes 0! is defined as being equal to 1. Let’s see why. Writing this out using the definition of factorials.

29. Counting Outcomes 0! is defined as being equal to 1. Let’s see why. Writing this out using the definition of factorials.

30. Counting Outcomes 0! is defined as being equal to 1. Let’s see why. Writing this out using the definition of factorials. so, the next logical conclusion is that

31. Counting Outcomes End of Lesson!