This document describes research on optimizing the design of induction motors using genetic algorithms. It presents three optimal motor designs that were compared to a classically designed motor with the same ratings. The genetic algorithm optimization considered three objective functions: efficiency, torque, and cost. Key design variables like stator and rotor dimensions were selected as variables to be optimized. Performance constraints like efficiency, power factor, and current densities were also defined. The optimal designs found by the genetic algorithm were intended to improve performance while reducing costs compared to the classical design approach.

1. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
443
COST AND PERFORMANCE OPTIMIZATION OF INDUCTION
MOTOR USING GENETIC ALGORITHM TECHNIQUE
A. S. Sindekar1
, A. R. Agrawal2
1
Dept.of Electrical Engineering, Govt. College of Engineering, V.M.V. Road, Amravati,
India
2
Dept.of Electrical Engineering, Govt. College of Engineering, V.M.V. Road, Amravati,
India
ABSTRACT
This paper presents three different optimal designs of induction motor. The optimally
designed motor is compared with classically designed motor, having same ratings. Genetic
Algorithm is used for optimization and three objective functions namely efficiency, torque
and cost are considered. The motor design procedure consists of a system of non-linear
equations, which gives induction motor characteristics, motor performance, magnetic stresses
and thermal limits. Genetic Algorithms (GAs) give satisfactory results in the design
optimization of electrical machinery, it has been observed that the GAs locate the global
optimum region faster than the conventional direct search optimization techniques.
Nowadays optimization of induction machine is making trade-off between different
objectives such as a particular item of performance, cost of machine or quality or reliability.
Keywords: Optimization Technique, Genetic Algorithm, Induction Motor.
1. INTRODUCTION
Induction motors have always played and will continue to play an important role in
the industry due to their simple structure, robustness [7, 11] and high reliability. It has
become a kind of demand by both the users and the manufacturers to optimize the design to
improve the performance in terms of efficiency, torque and reduce the active material which
comprises cost of the induction motor. Because the optimization of induction motor design is
highly nonlinear mix-discrete constrained multivariable problem, the conventional
INTERNATIONAL JOURNAL OF ELECTRICAL ENGINEERING
& TECHNOLOGY (IJEET)
ISSN 0976 – 6545(Print)
ISSN 0976 – 6553(Online)
Volume 4, Issue 2, March – April (2013), pp. 443-449
© IAEME: www.iaeme.com/ijeet.asp
Journal Impact Factor (2013): 5.5028 (Calculated by GISI)
www.jifactor.com
IJEET
© I A E M E

2. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
444
optimization methods, are not effective. On the other hand genetic algorithm shows
remarkable effects and is being widely used for solving the optimization problems for
electrical machines and other electromagnetic devices. If the standard non-linear
programming (NLP) techniques were to be used in this case, then they would be
computationally very expensive, time consuming and inefficient. GA’s have been renowned
as an important tool in design optimization of electrical machinery in recent years. One of the
most important advantage of the GA over the standard NLP techniques is that it is able to
find the global minimum, instead of a local minimum. Another advantage is that it does not
require derivative of the function, which is not always easily obtainable or may not even
exist. The aim of this paper is to give a further contribution in the optimum design of three
phase induction motor in manufacturing process; using three objective functions, namely cost
(C), efficiency (E) and torque (T). A design sheet has been developed for a particular three-
phase squirrel-cage type induction motor. An induction motor of 2.2 kW, 400 V, 1500
synchronous r.p.m. is chosen for comparison with three optimally designed motors [12].
Same motor rating (basic specification) is used for three optimal designs and same
performance limits (constraints) are considered for all three designs. Advantages and
disadvantages of each design are then briefly discussed.
2. BASICS OF GENETIC ALGORITHM
Genetic Algorithm is a random search method [10] which involves stochastic
generation of several valid design solutions and then systematically validates and refines the
solutions until a stopping criterion is met. There are three fundamental operators which
comprise in the search process of genetic algorithm: selection, crossover, and mutation.
Following are the steps to implement GA:
Step 1: Define all parameters involved and form objective function
Step 2: Generate first population at random
Step 3: Check and validate population on the basis of fitness value of objective function
Step 4: Test the solution. If satisfied then stop else continue.
Step 5: Apply all GA operators (Selection, Crossover, and Mutation)
Step 6: New generation is obtained, to continue the optimization return to step 3.
Selection: Selection is a process in which individual chromosomes (combination of
parameters) are selected according to their fitness value. The selection probability [1] can be
defined by
Pj = F (xi) / ∑ i
F (xi)
Where Pj is probability of selection of certain individual string and F (xi) is objective
function.
Crossover: This is the most powerful genetic operator. There are two types of crossover,
single-point crossover and multi point crossover. Usually single-point crossover is used.
Following is an example of single-point crossover; crossover point is selected between the
first and the last bits of the parent chromosome. The binary code which is to the right of the
crossover point of Parent1 goes to Offspring2 [1] and Parent2 passes its code to Offspring1.

3. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
445
Point of crossover
Parent1 = 0010010 101
Parent2 = 0101011 100
Offspring1 = 0010010 100
Offspring2 = 0101011 101
Mutation: This is a common genetic shuffling operator, which involves the stochastic
alteration of genes [2] during the process of copying a chromosome from one parent to its
offspring. The mutation operator should be used because, mutation increases algorithm’s
freedom to search outside the current region of parameter space. Mutation changes from a
“0” to a “1” or vice versa. It may be illustrated as follows:
110001010 › 110000010
3. PROBLEM FORMULATION
a) Objective functions
As mentioned earlier there are three objective functions, cost of the motor, efficiency
of the motor and torque of the motor.
i) Objective function for cost
Total cost of motor [3, 8] is addition of copper material cost, iron material
cost, fabrication cost and laminating cost. Lamination cost for low and mid range motors is
around 150% of total active material cost and fabrication cost is around 25% of total motor
cost. For formulation purpose only cost of active material (addition of copper cost and iron
cost) is used as a function. The cost of copper or iron depends on its weight and weight
depends on the volume. Volume is a function of area and length. Iron weight and copper
weight is multiplied by per kg rate of Rs.50 and Rs.450 respectively, thus cost objective
function is written as:
Cost of active material [fun(y)] = [(weight of iron * 50) + (weight of copper * 450)]
ii) Objective function for efficiency
Efficiency is the ratio of output and input of the motor [4]; so mainly we need
to calculate the output and all losses such as copper losses, iron losses and friction and
windage losses. Moreover for considering the additional losses such as harmonic losses,
pulsation losses, 0.5 is deducted from the equation for efficiency. So the required objective
function will be:
Efficiency [fun(y)] =
output
output + losses
Efficiency [fun(y)] =
PW×1000
ሺPW×1000ሻ+total loss
×100 - 0.5

4. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
446
iii) Objective function for torque
The objective function is given by:
Torque at full load [fun(y)] =
rotor input × 60
2× π×Ns
Where Ns is synchronous speed in r.p.m. and rotor input is the addition of rotor output,
friction and windage losses and rotor copper losses. Thus we need to calculate these
parameters with MATLAB program.
bሻbሻbሻbሻ Design variables:
Practically there are many parameters in induction motor design which can be
considered as design variables. Some key independent variables are selected and are assigned
from X1 to X13 with their upper and lower bounds [9].
Table 1: Design Variables
c) Inequality constraints
Some key performance parameters [5] are considered with their upper and lower
bounds [9] as inequality constraints. The performance parameters are taken as constraints
only to have a practical optimal design (feasible design), which has an optimal value of the
considered objective function with all the performance parameters within the specified limits.
Table 2: Performance Constraints (limits)
Variable Parameter Upper
limit
Lower
limit
X1 Stator turns per phase 480 400
X2 Length of stator core (m) 0.13 0.11
X3 Diameter of stator core (m) 0.110 0.105
X4 Stator slot height (mm) 20 15
X5 Stator tooth width (mm) 6 3
X6 Depth of rotor slot (mm) 10 9
X7 Width of rotor slot (mm) 8 6
X8 Actual diameter of stator conductor (mm) 0.96 0.90
X9 Area of each rotor bar (mm2
) 45 43
X10 Depth of end ring (mm) 11 8
X11 Thickness of end ring (mm) 9 7
X12 Depth of rotor core (mm) 18 15
X13 Length of air gap (mm) 0.35 0.29
Variable Parameter Upper
limit
Lower
limit
b1 Efficiency (%) 85 80
b2 Power factor 0.9 0.8
b3 Full load slip (%) 6 3
b4 Rotor bar current density (A/mm2
) 6 4
b5 Stator current density ( A/mm2
) 5 3.9
b6 Starting current (A) 19 15
b7 Starting torque (N-m) 17 14

5. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
447
4. EXECUTION OF PROBLEM
Classical design of induction motor is carried out with MATLAB. Simple program is
written for obtaining all the required design parameters. The values of all three objective
functions are calculated without applying any optimization technique (classically). Genetic
algorithm tool box is used to optimize the objective functions of cost, efficiency and torque.
The fitness function (objective function) is written as @name of m. file in which function is
saved, then the total number of variables used is mentioned in the next row and finally the
linear inequalities are written in the matrix form.
5. RESULTS
In table 3 values of all design variable, for classical design, efficiency optimization,
cost optimization and torque optimization is given. Table 4 shows, values of all performance
parameter for all three optimization and classical design. Both the tables give a comparative
evaluation of all results obtained.
Table 3: Comparative values of design variable
Table 4: Comparative values of performance parameter
Variable Parameter Classical
design
Efficiency
optimization
Cost
optimization
Torque
optimization
X1 Stator turns per phase 416 408 433 440
X2 Length of stator (m) 0.125 0.123 0.120 0.120
X3 Diameter of stator core (m) 0.105 0.1055 0.105 0.109
X4 Stator slot height (mm) 17 15 15 19.98
X5 Stator tooth width (mm) 3.9 3 3 3
X6 Depth of rotor slot (mm) 9.3 10 9 10
X7 Width of rotor slot (mm) 6.8 6 6.057 7
X8 Actual diameter of conductor (mm) 0.95 0.936 0.91 0.90
X9 Area of each rotor bar (mm2
) 44 44.56 43 43
X10 Depth of ring (mm) 10 8 8 10.99
X11 Thickness of ring (mm) 8 9 7 7
X12 Depth of rotor core (mm) 17 17 16 16.21
X13 Length of air gap (mm) 0.3 0.31 0.29 0.314
Parameter Classical
design
Efficiency
optimization
Cost
optimization
Torque
optimization
Efficiency (%) 81.3 83.93 80.5 79.9
Power factor 0.829 0.865 0.81 0.89
Full load slip (%) 5.6 3.06 3.04 3.009
Rotor bar current density (A/mm2
) 4 4.50 4.001 4.003
Stator current density (A/mm2
) 3.9 3.95 3.89 4.08
Starting current (A) 18.86 18.37 19 17.68
Full load torque (N-m) 15 14.89 15.06 15.25
Starting torque ( N-m) 15 14.80 15.04 15.25
Active material cost (INR) 2600 2570 2348 2630

6. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
448
6. CONCLUSION
Optimization of all three objective functions is carried out with the help of GA
toolbox which gives effective and fast results in comparison with the MATLAB GA program.
At the time of optimization many constant parameters can also be taken into consideration as
design variables or performance parameters. Apart from the three objective functions chosen
in this paper, power factor can also be considered as an objective function for maximization.
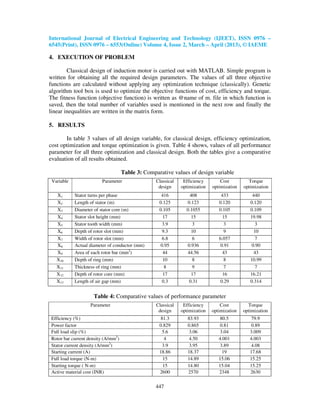
With respect to the results shown in table 3 and table 4, following conclusions can be drawn:
1. Active material cost is reduced by almost 10% with all the performance parameters
within their specified limits.
2. Almost 3% increase is seen in efficiency as compared to the classically designed
motor that to with a better cost. It can be further increased by improving the quality
of active material used.
3. Full load torque goes up by almost 2% with torque optimization, with the highest
cost and lowest efficiency amongst all four.
4. All three optimal designs obtained can be fabricated (assembled) by using the frame
size ‘D100L’, which is a standard frame size for this rating.
5. Diameter of stator core and length of stator changes slightly in all three optimal
designs; however the same frame size can be used.
6. In efficiency optimized design, stator turns per phase are less than that of the
classical design which will slightly affect the loading capacity of the motor. This
problem can be resolved either by making new stator stampings according to the new
dimensions obtained or by slightly increasing the actual diameter of conductor used.
Making new stator stamping is affordable only when there is a bulk order of motor
manufacturing.
7. In cost and torque optimized designs, stator turns per phase are greater than that of
the classical design those can be accommodated in the same slots of stampings by
slightly decreasing the diameter of conductor.
8. There are minor changes in the width and depth of rotor slot in all the three optimal
designs. This results into change in the starting torque of the motor. End ring current
is not investigated.
REFERENCES
[1] Mehmet Cunkas and Ramazan Akkaya, “Design Optimization of Induction Motor by
Genetic Algorithm and Comparison with Existing Motor”, Mathematical and
Computational Application, Vol. 11, No. 3, pp 193-203, 2006
[2] Li HAN, Hui LI, Jingcan LI, Jianguo ZHU, “Optimization for Induction Motor Design
by Improved Genetic Algorithm”, Australasian Universities Power Engineering
Conference, pp 26-29 September 2004
[3] Shivendra Prakash Verma, “Design Optimization of 7.5 Kw, 4 Pole, 3-Phase, 50 Hz
Induction Motor Employing Genetic Algorithm / Improved Genetic Algorithm Using
Sweep Frequency Response Analysis”, MIT International Journal of Electrical and
Instrumentation Engineering Vol. 1, No. 2, Aug. 2011, pp 108-115 ISSN 2230-7656©
MIT Publications.
[4] S. Ghozzi, K. Jelassi, X. Roboam, “Energy optimization of induction motor drives”,
IEEE conference on industrial technology, 2004

7. International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 –
6545(Print), ISSN 0976 – 6553(Online) Volume 4, Issue 2, March – April (2013), © IAEME
449
[5] J. Faiz, M.B.B. Sharifian, “Optimal design of three phase induction motors and their
comparison with a typical industrial motor”, Int. J. of Comp. and Elect. Engg. Eng.
27:133-144, 2001
[6] X. Liu, G. R. Slemon, “An Improved Method of Optimization for Electrical
Machines”, IEEE Trans. On energy conversion, Vol. 6, no. 3, pp 492-496, sep. 1991
[7] C.G. Veinott, Theory and Design of Small Induction Motors, McGraw-Hill, New
York, 1959.
[8] M. Ramamoorty, “Computer Aided Design of Electrical Equipment”, Affilated East
West Press Private Limited, New Dehli, 1987, pp 1 -4, 86-94
[9] A Shanmugasundaram, G Gangadharan, R Pillai, “Electrical Machine Design Data
Book” New Age International Pvt. Ltd., New Dehli, 2001
[10] D.E. Goldberg, “Genetic Algorithms in Search, Optimization, and Machine Learning”,
Addison Wesley, New York, 1989.
[11] S.J. Chapman, “Electric machinery and power system fundamentals”, McGraw-Hill,
New York, 2002.
[12] A. K. Sawhney, “A Course in Electrical Machine Design”, Dhanpat Rai and Sons,
New Delhi, 5th Edition, 1991, pp 10.1-10.97, 22.1-22.7.