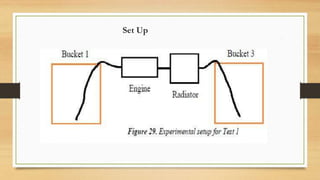
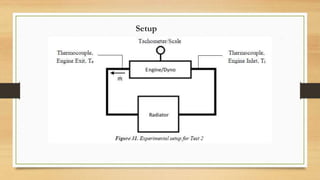
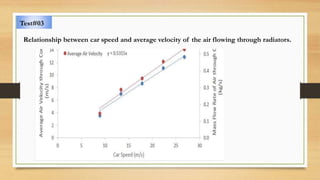
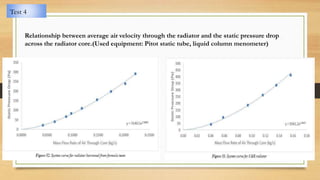
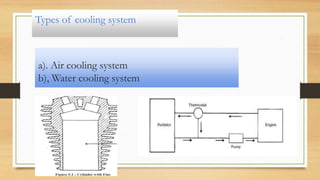
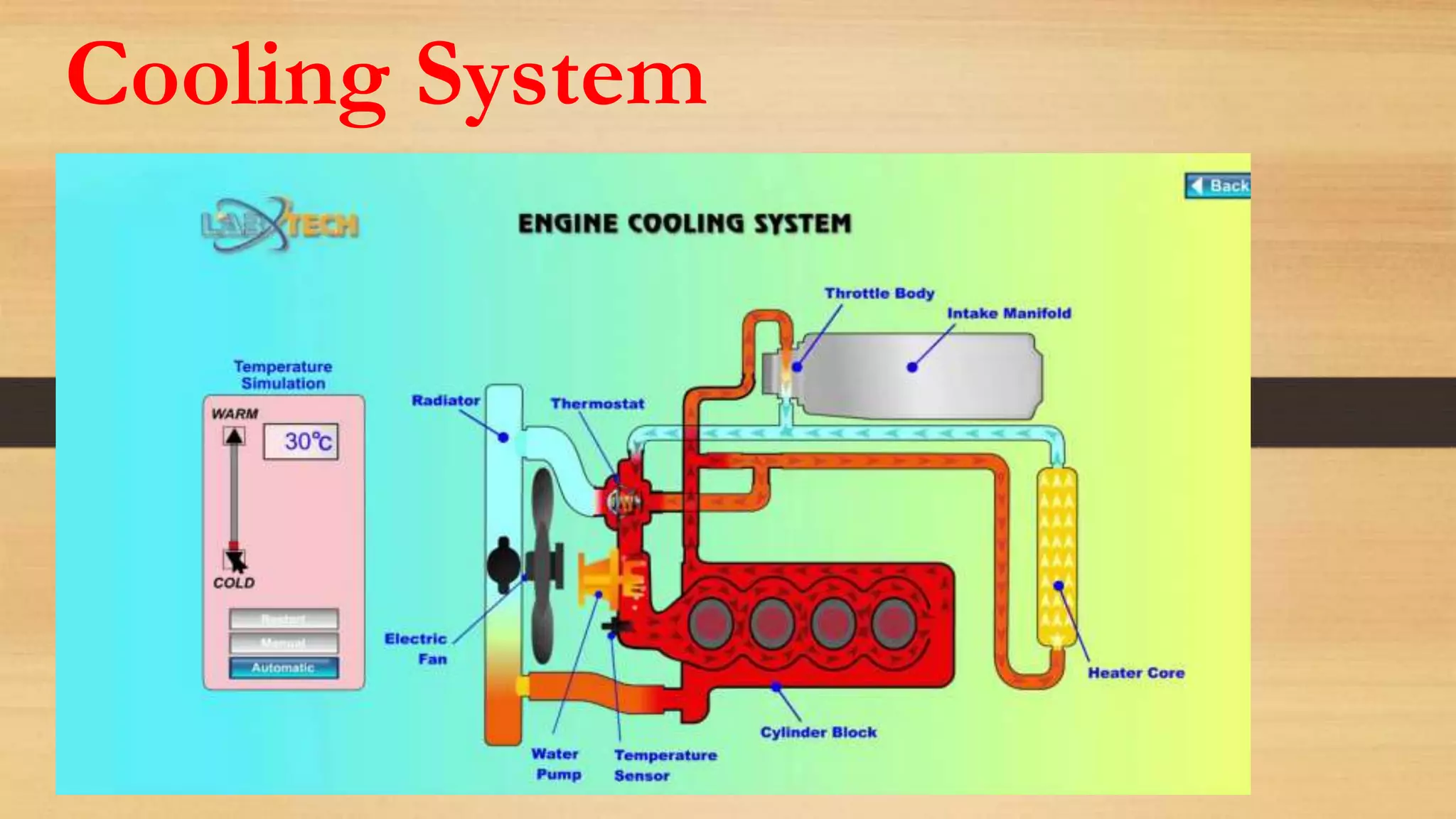
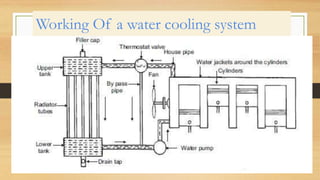
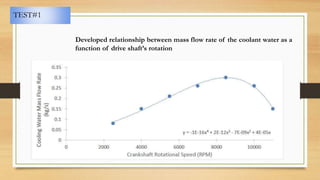
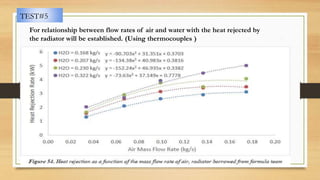
The document discusses various aspects of engine cooling systems, including: 1) Different types of cooling systems like air cooling and water cooling are described. Water cooling further includes thermosiphon and pump circulation systems. 2) Key components of a water cooling system are identified, including the coolant, pump, thermostat, radiator, reserve tank, and fan. 3) Techniques for sizing radiators are outlined, including establishing relationships between various parameters through testing and using effectiveness-NTU or LMTD methods. Worst case scenarios can be used to determine required heat rejection and radiator size.

1. Cooling System

2. ● Temperature of burning gases can reach up to 1500-2000 c which
is greater than melting point of block material.
● Without coolant system, any engine would destroy in a while.
● Engine has a specific temperature interval in which it does its great
job.(195-220 F)
● Basically a coolant is circulated in the engines which maintains its
temperature.

3. Things to be noted:
a). About 20-25% generated heat is used in brake power.
b). About 30% of generated heat goes in coolant
c). Rest goes in friction loses and exhaust.

4. a). Air cooling system
b), Water cooling system
Types of cooling system

5. Air cooling System
Advantage:
● Cheaper, simple, Inexpensive
● the heat, which is conducted to the outer parts of the
engine, is radiated and
● conducted away by the stream of air, which is
obtained from the atmosphere.
Used in low power engine(15-20 KW) and in aero plane engine.

6. Water Cooling system

7. Types of water cooling system
a). Thermo Siphon System of Cooling
b).Pump Circulation System

8. Thermo Siphon System of Cooling
In this system the circulation of water is due to difference in temperature
(i.e. difference in densities) of water. So in this system pump is not
required
but water is circulated because of density difference only.

9. Coolant system using pump
In this system circulation of water is obtained by a pump. This pump is
driven by means of engine output shaft through V-belts.

10. Working Of a water cooling system

11. Parts of a Cooling System

12. 1. Coolant
2. Pump
3. Thermostat
4. Radiator
5. Reserve tank
6. Radiator cooling Fan
7. Pressure cap
8. Freeze Plug
9. Head gasket
10.Hoses
11.Bypass system

13. Coolant + Antifreeze
● What are they
● FSAE Rule

14. Story for illustration purposes only
Pump
Thermostat
Freeze Plug
Head Gasket

15. Radiators
Heat Exchanger
Design is most important aspect because it is in our hand.
Cross flow and down flow type radiator
Pressure Cap

16. Designing of Cooling system
Variables
● Number, Size, type, orientation of radiators
● Mass flow rate of water and air
● Size, Number, Place of Fan
● Ducting in and out of the radiator
● Pressure drop across the radiator/rise across the flow
But still we would rely on the size and numbers of radiators.

17. Specifications of KTM390
● 4 stroke, single cylinder
● Water cooled
● Rated Power 43HP
Calculations of Size of radiators
Let us see….

18. Technique #1
Reference: Formula SAE design report
Overview
They conducted experiments on real radiator using engine dyno technique in
wind tunnel and find out relationships between many variables as:
Mass flow rate of coolant, mass flow rate of air, crankshaft speed, car speed,
rate of heat dissipation and using worst case scenario and find out required area
of radiator which would be involved in heat exchanging.

19. TEST#1
Developed relationship between mass flow rate of the coolant water as a
function of drive shaft’s rotation

20. Set Up

21. Test 2
Relationship between rate of rotation of crankshaft and the rate at which heat is
rejected from the engine to the cooling water.
About 30%
of the engine
power
converter
into heat
dissipation.

22. Setup

23. Test#03
Relationship between car speed and average velocity of the air flowing through radiators.

24. Procedure
Three people would be required to collect data. One person will drive
the car, then one person will hold the radiator outside of the
window while another person held the anemometer behind the
radiator to collect data

25. Test 4
Relationship between average air velocity through the radiator and the static pressure drop
across the radiator core.(Used equipment: Pitot static tube, liquid column menometer)

26. Conclusion:
The calibration curves above suggest that the pressure drop across the C&R core is
significantly higher than the pressure drop across the other radiator at an equivalent air mass
flow rate.
This is due to higher fin density associated with the C&R core.
There are more fins and thus more drag resulting in more significant head losses across the
core.
This is reflected by a loss in static pressure between the two sides of the core.

27. TEST#5
For relationship between flow rates of air and water with the heat rejected by
the radiator will be established. (Using thermocouples )

29. Using Experimental results to size the
radiator
Worst case scenario: This “worst-case scenario” is the operating point that results in a
high rate of heat rejection from the engine to the cooling fluid and
a low rate of heat rejection from the cooling fluid to the air via the radiator.
Solution: Car should be in 1st year and at maximum speed so that velocity of air
passing through radiator is less and power output is high.
V: var velocity
Ne: Crankshaft RPM
Et: transmission reduction
Ea: drive axle reduction
Rw: radius of the tire

30. Process: 1. From car speed, determine mass flow rate of air.(Test 3)
2. From mass flow rate of air or mass flow rate of water, determine heat
rejection rate through cooling water.( Test 5)
3. The heat rejection rate measured in Test 5 can be viewed as the heat rejection
rate per heat transfer area (or the surface area of the fins contained within the duct during
testing).
4.To determine the surface area necessary to achieve adequate cooling, simply
divide the rate at which heat is rejected from the engine to the water by the rate of heat
rejection from the water to the air per unit area, according to
Equation 6 as follows.
𝐴𝑟𝑒𝑞 = 𝐴ℎ𝑡 ∗(Q2/Q5)

31. Technique#2
Effectiveness: NTU Method
U.A
NTU = ---------
C(min)
U: heat exchanger coefficient
A: heat exchanger surface
area

33. 1. The value of the effectiveness ranges from 0 to 1.
2. It increases rapidly with NTU for small values (up to about NTU 1.5) but
rather slowly for larger values. Therefore, the use of a heat exchanger with a
large NTU (usually larger than 3) and thus a large size cannot be justified
economically, since a large increase in NTU in this case corresponds to a small
increase in effectiveness.
3.Thus, a heat exchanger with a very high effectiveness may be
highly desirable from a heat transfer point of view but rather undesirable from
an economical point of view.

34. 4. The effectiveness of a heat exchanger is independent of the capacity ratio c for NTU
values of less than about 0.3.
5. The value of the capacity ratio c ranges between 0 and 1. For a given NTU, the
effectiveness becomes a maximum for c = 0 and a minimum for c = 1.
The case c = Cmin /Cmax → 0 corresponds to Cmax →∞ , which is realized
during a phase-change process in a condenser orboiler. All effectiveness relations in this
case reduce to ε = εmax = 1 - exp(NTU) regardless of
the type of heat exchanger.
6. Note that the temperature of the condensing or boiling fluid remains constant in this
case.

35. Technique# 3
• The logarithmic mean temperature difference(LMTD)
• LMTD method is very suitable for determining the size of a heat
• exchanger to realize prescribed outlet temperatures when the
massflow
• rates and the inlet and outlet temperatures of the hot and cold fluids
are specified