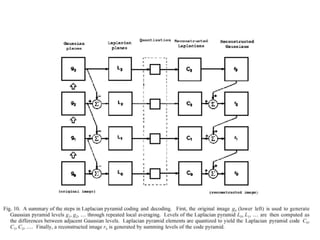
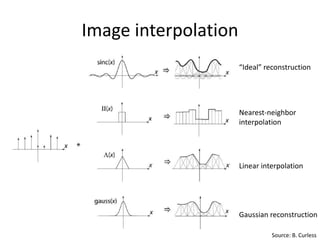
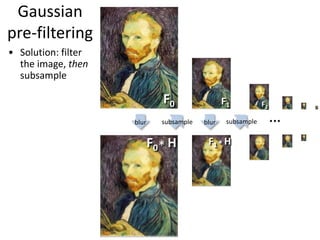
This document discusses techniques for image resampling and interpolation. It begins with a basic explanation of image subsampling which can cause aliasing artifacts. It then introduces Gaussian pre-filtering as a way to avoid aliasing by smoothing high frequencies before subsampling. The Gaussian pyramid is presented as a multi-scale image representation built from successive Gaussian filtering and subsampling steps. Upsampling is also discussed, along with various interpolation methods like nearest neighbor, bilinear, and bicubic interpolation that can be used to increase image resolution. Modern learning-based super resolution techniques are briefly mentioned at the end.















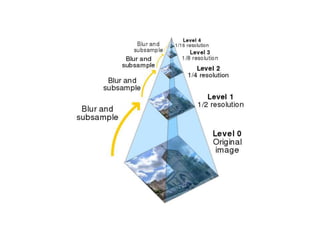
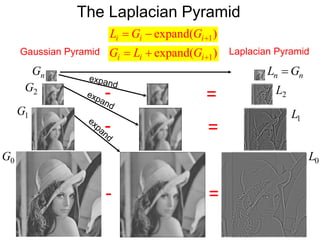
![Gaussian pyramids
[Burt and Adelson, 1983]
• In computer graphics, a mip map [Williams, 1983]
• A precursor to wavelet transform
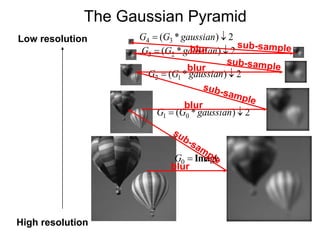
Gaussian Pyramids have all sorts of applications in computer vision
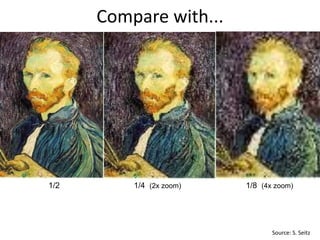
Source: S. Seitz](https://image.slidesharecdn.com/lec03resample-200719134934/85/Computer-Vision-resample-21-320.jpg)
![Gaussian pyramids
[Burt and Adelson, 1983]
• How much space does a Gaussian pyramid take compared to the
original image?
Source: S. Seitz](https://image.slidesharecdn.com/lec03resample-200719134934/85/Computer-Vision-resample-22-320.jpg)