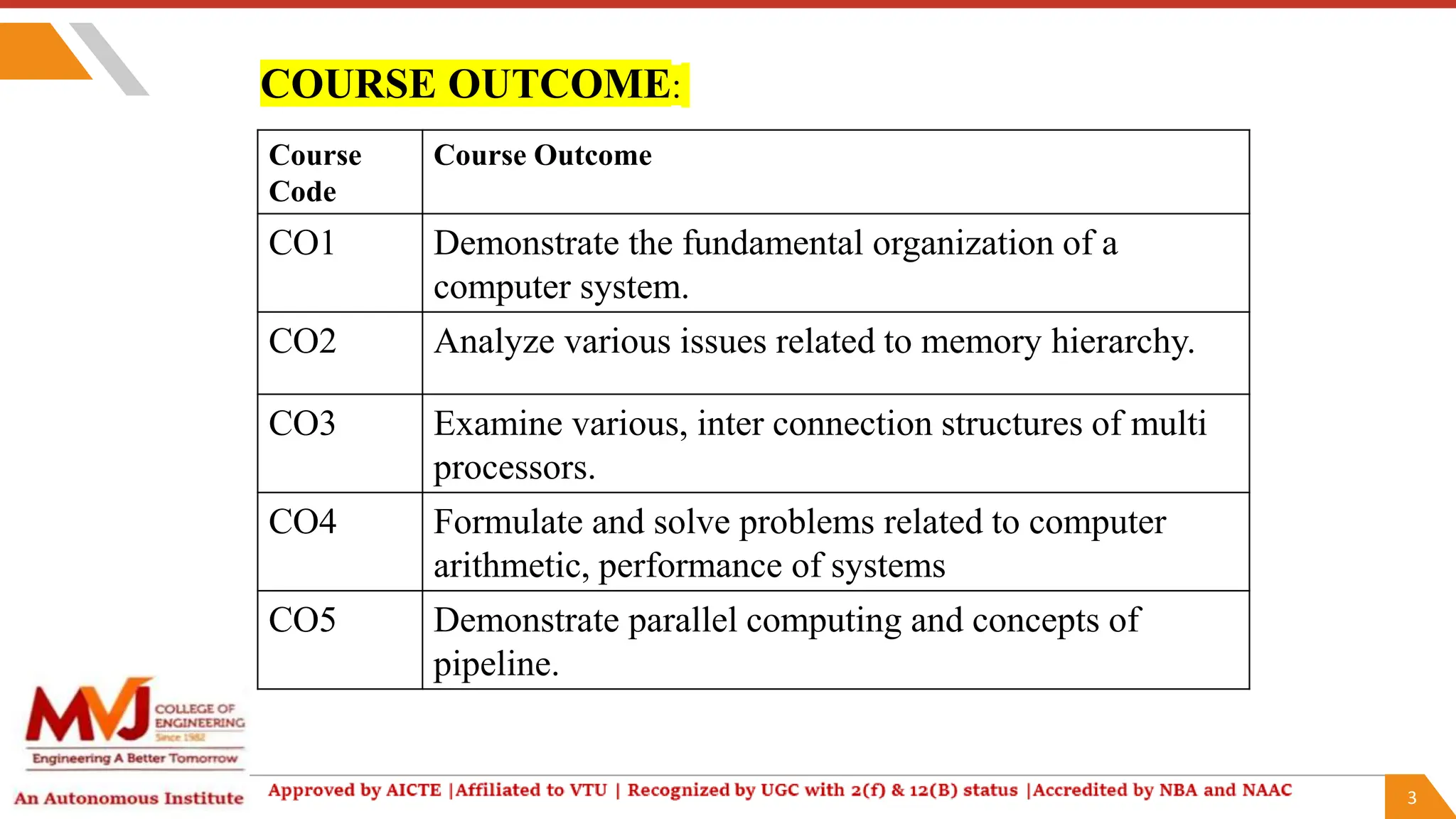
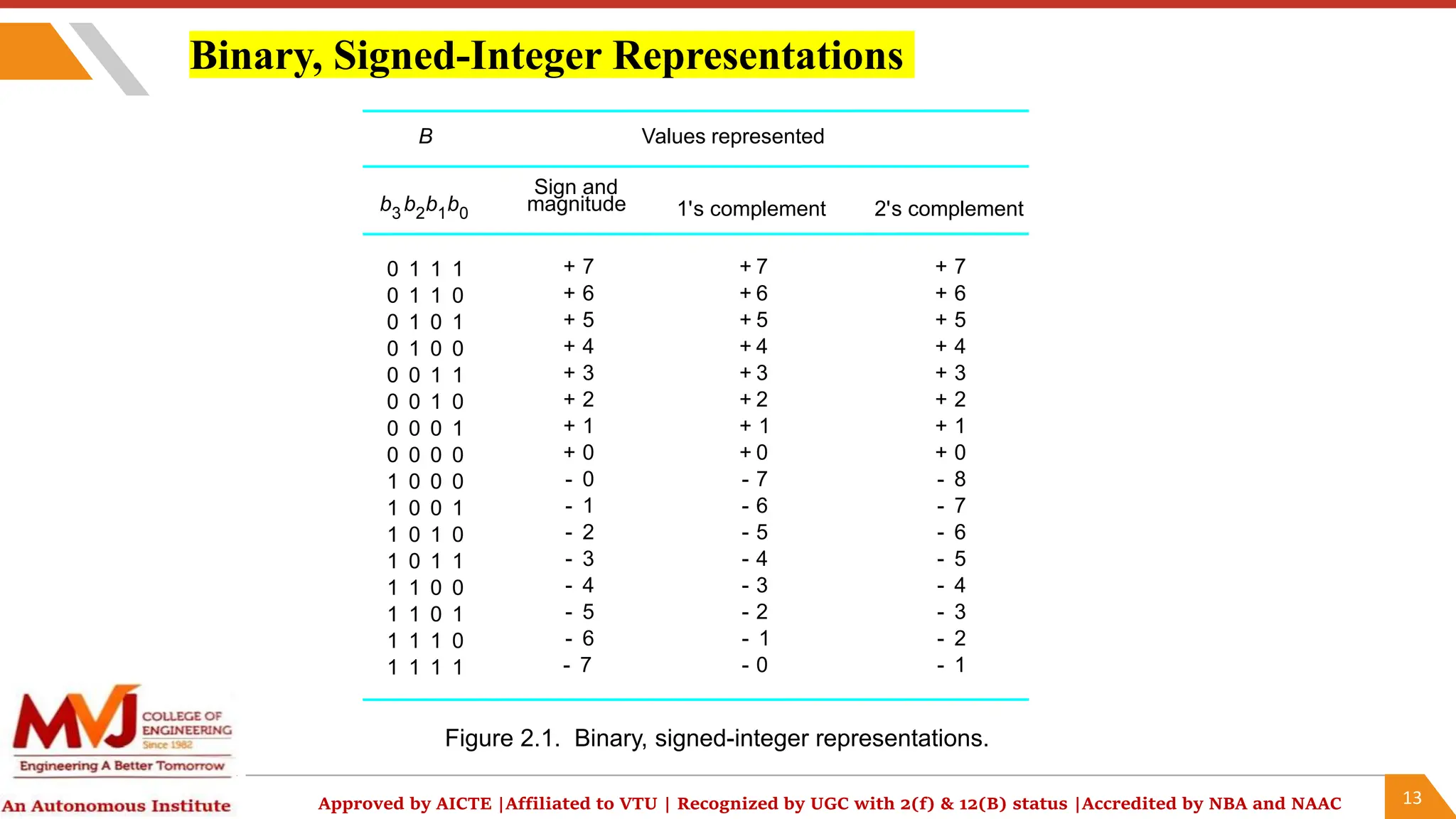
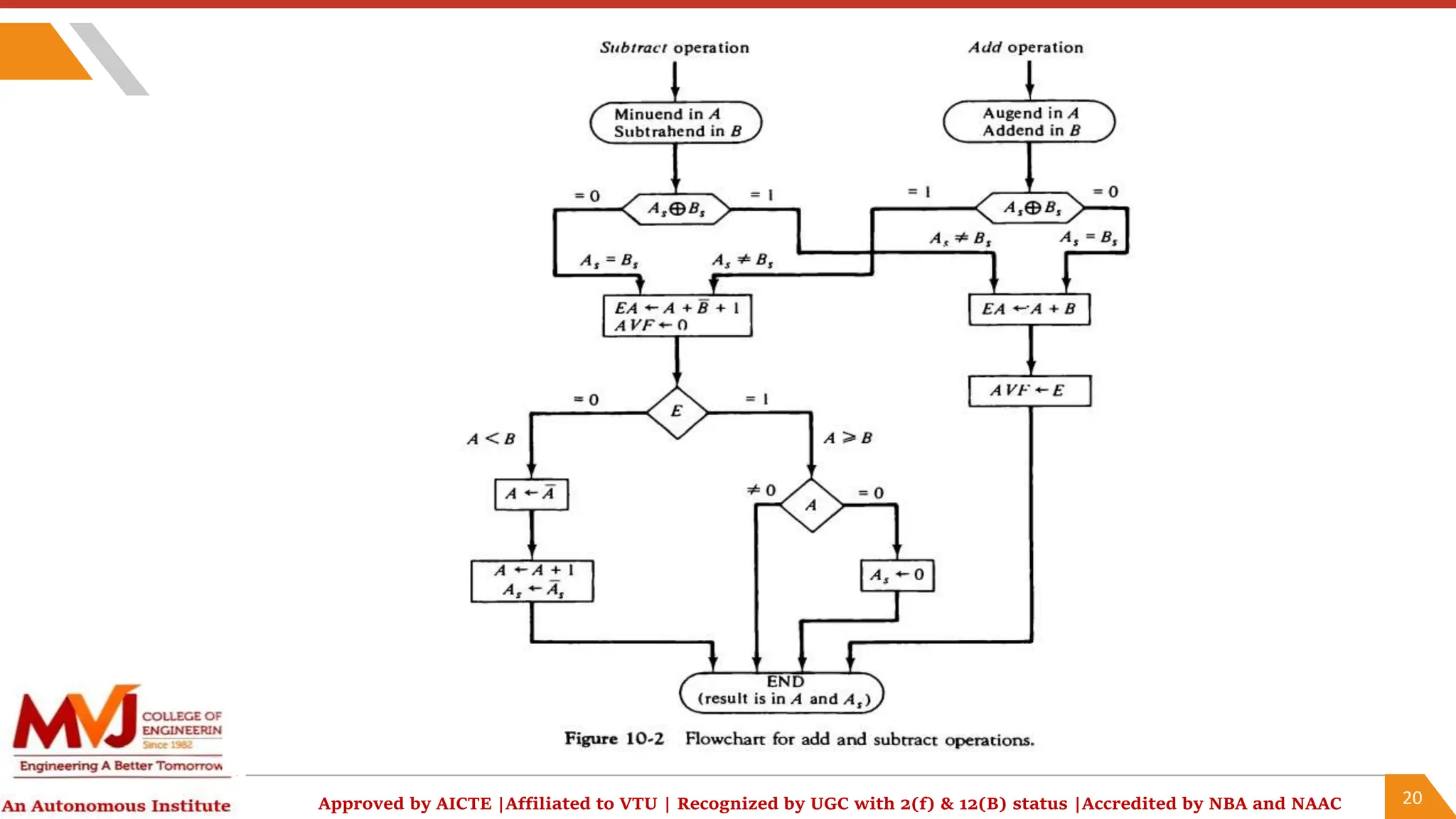
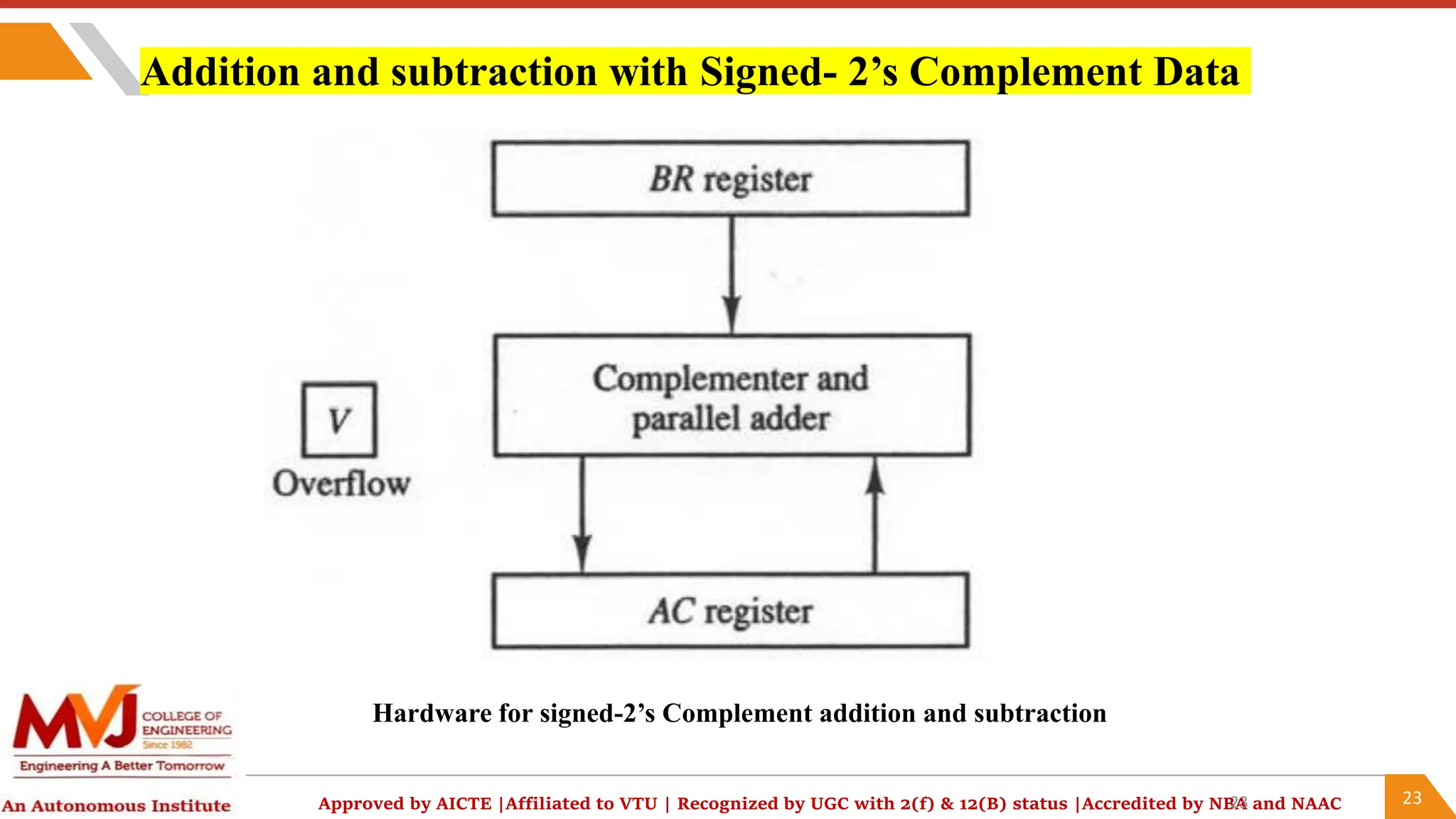
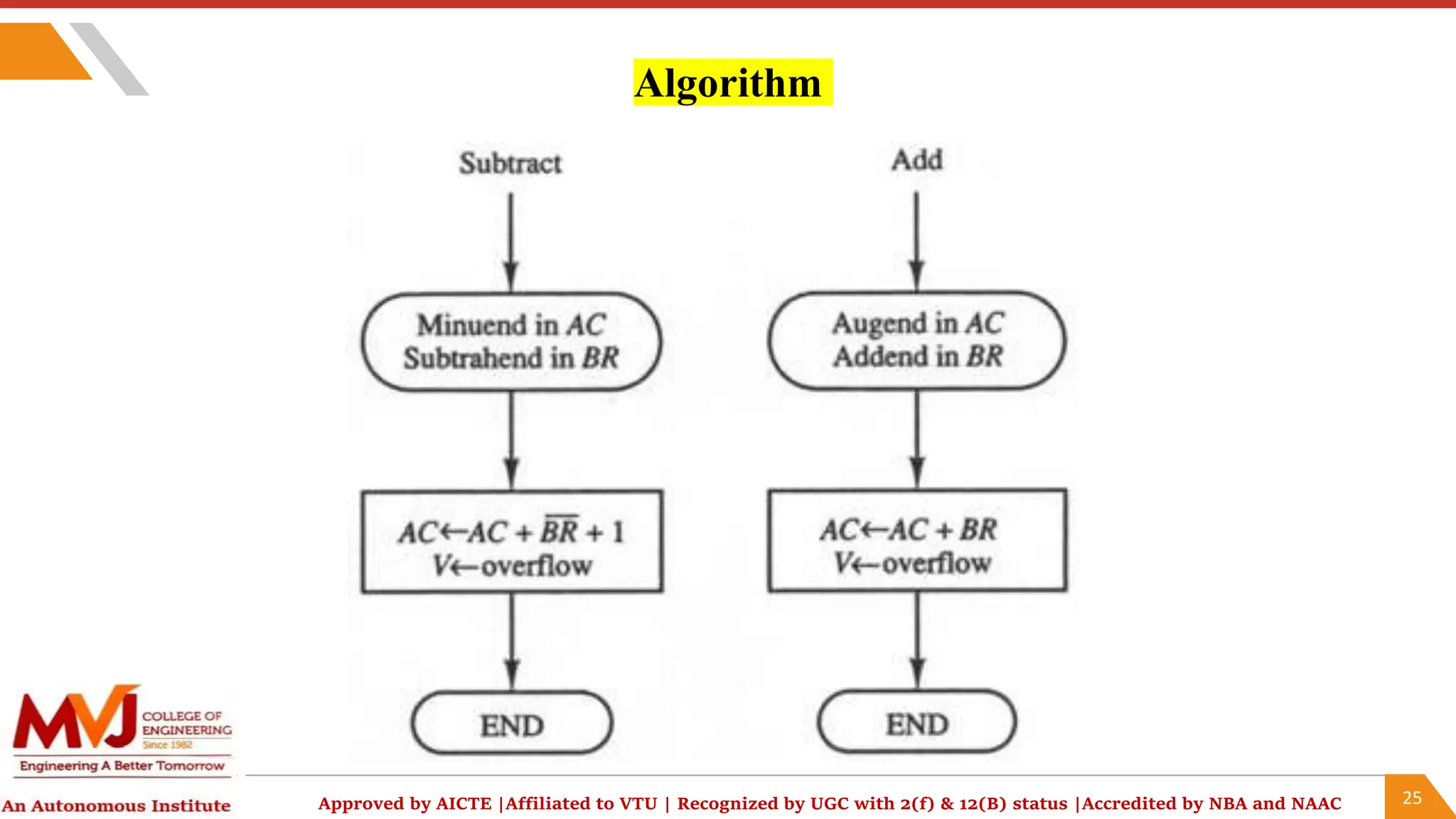
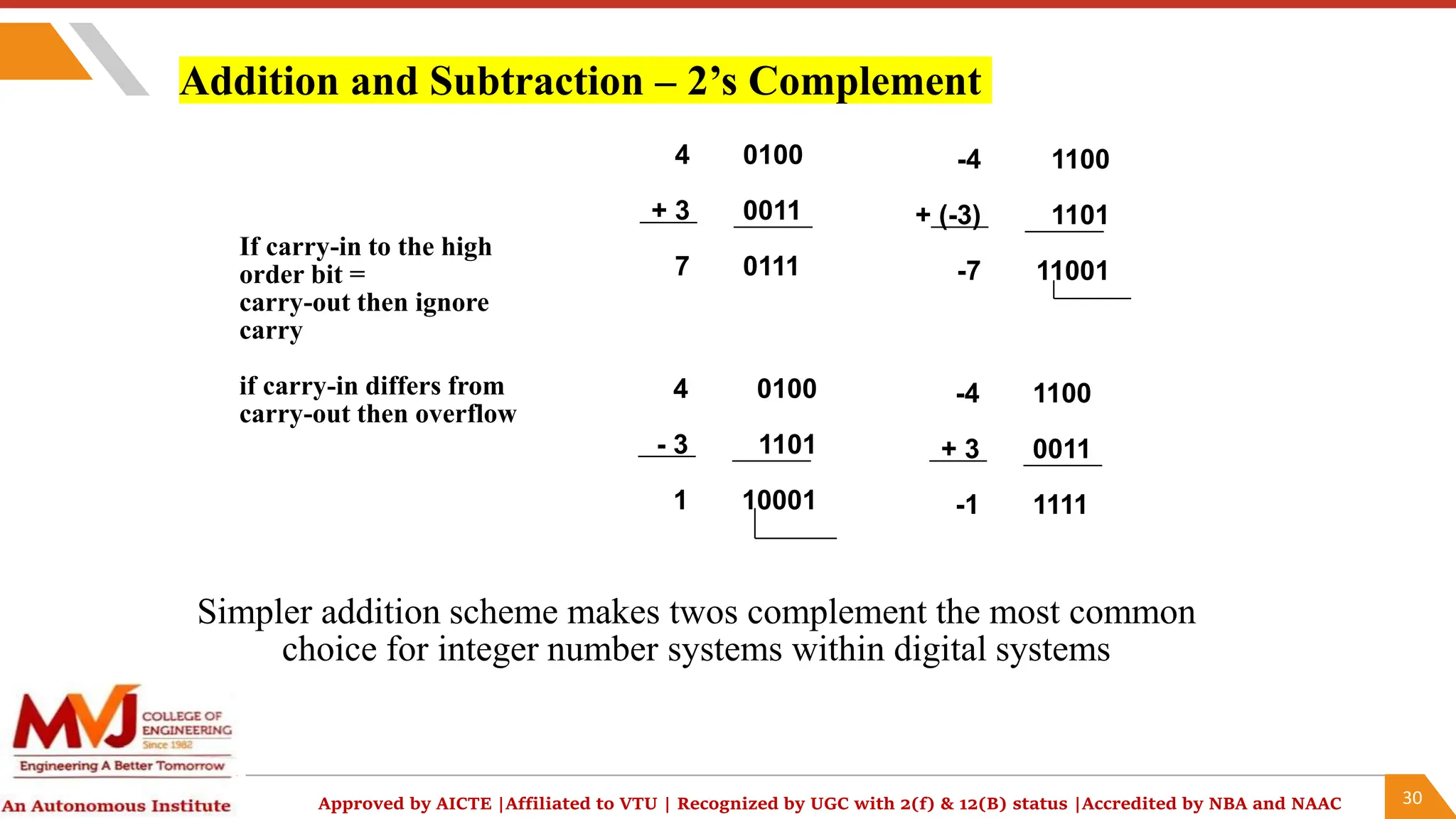
The document outlines a computer organization and architecture course that includes objectives, outcomes, and detailed topics such as number systems (decimal, binary, octal, hexadecimal), arithmetic operations, and representations of signed integers. It highlights various ISA styles, memory hierarchy issues, and techniques for parallel computing and problem-solving in computer arithmetic. Additionally, it provides examples and algorithms for addition and subtraction using different signed number representations.