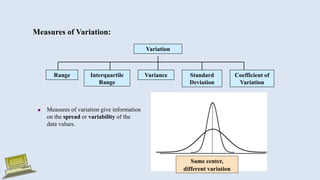
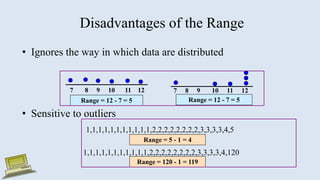
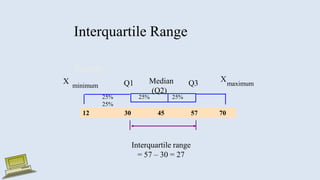
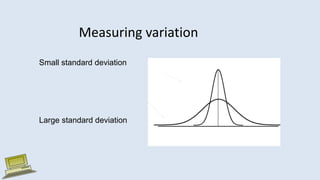
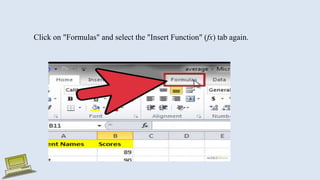
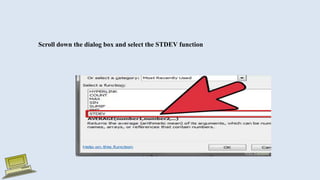
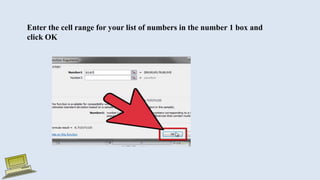
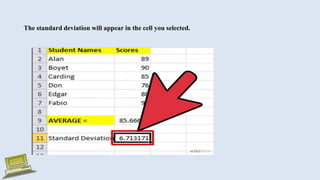
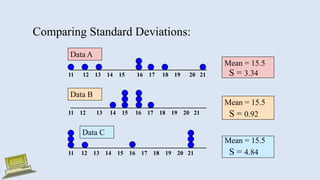
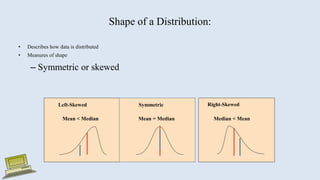
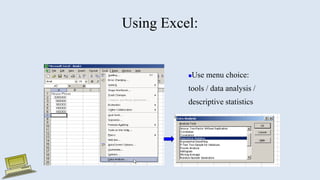
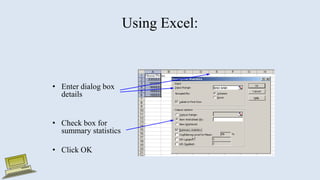
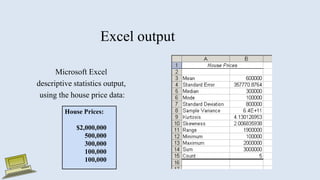
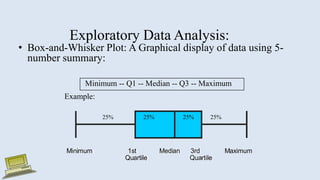
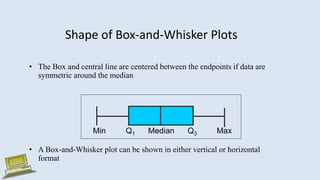
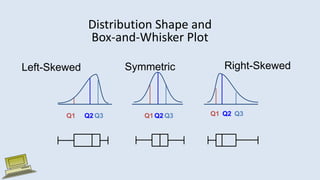
The document discusses various measures of statistical variation that can be used to analyze and describe the spread or dispersion of data values in a data set. It defines and provides examples to calculate and interpret range, standard deviation, variance, interquartile range, and coefficient of variation. It also discusses box plots and how they can be used as a graphical method to visualize the five number summary of a data set. Microsoft Excel functions like STDEV and descriptive statistics tools are demonstrated for computing some of these measures of variation from a data set.