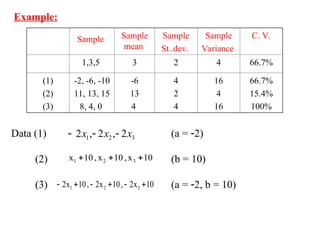
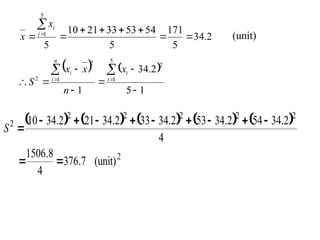The document discusses measures of dispersion, particularly focusing on range, variance, standard deviation, and coefficient of variation, explaining how these metrics indicate the spread of values in a dataset. It provides formulas to calculate population and sample variance, standard deviation, and illustrates their significance through examples. Additionally, it highlights the importance of the coefficient of variation for comparing relative variability across different datasets.

1. Larger variation
2.3. Measures of Dispersion (Variation):
The variation or dispersion in a set of values refers to how spread
out the values are from each other.
· The variation is small when the values are close together.
· There is no variation if the values are the same.
· Same
Center
Smaller variation
Smaller variation
Larger variation

2. Some measures of dispersion:
Range – Variance – Standard deviation
Coefficient of variation
Range:
Range is the difference between the largest (Max) and smallest (Min)
values.
Range = Max  Min
Example:
Find the range for the sample values: 26, 25, 35, 27, 29, 29.
Solution:
Range = 35  25 = 10 (unit)
Note:
The range is not useful as a measure of the variation since it only
takes into account two of the values. (it is not good)

3. Variance:
The variance is a measure that uses the mean as a point of reference
· The variance is small when all values are close to the mean.
· The variance is large when all values are spread out from the mean
Squared deviations from the mean:
X1
X2 x Xn
(X1
 )2
x (X2
 )2
x (Xn
 )2
x
(1) Population variance:
Let be the population values.
The population variance is defined by:
N
X
X
X ,
,
, 2
1 

4.        
N
X
X
X
N
X
N
N
i
i 2
2
2
2
1
1
2
2 














  (unit)2
where is the population mean.
N
X
N
i
i


 1

Notes:
· is a parameter because it is obtained from the population
values (it is unknown in general).
·
(2) Sample Variance:
Let be the sample values.
The sample variance is defined by:
2

0
2


n
x
x
x ,
,
, 2
1 
       
1
1
2
2
2
2
1
1
2
2













n
x
x
x
x
x
x
n
x
x
S N
n
i
i
 (unit)2

5. Where is the sample mean
n
x
x
n
i
i


 1
Notes:
· S2
is a statistic because it is obtained from the sample values (it
is known).
· S2
is used to approximate (estimate) .
·
Example:
We want to compute the sample variance of the following sample
values: 10, 21, 33, 53, 54.
2

0
2

S
Solution:
n=5

6. 2
.
34
5
171
5
54
53
33
21
10
5
5
1










i
i
x
x (unit)
   
1
5
2
.
34
1
5
1
2
1
2
2










 i
i
n
i
i x
n
x
x
S
         
(unit)
7
.
376
4
8
.
1506
4
2
.
34
54
2
.
34
53
2
.
34
33
2
.
34
21
2
.
34
10
2
2
2
2
2
2
2












S

7. Another method:
 




5
1
0
i
i x
x  
 
 8
.
1506
2
x
xi
i
x  
 
2
.
34



i
i
x
x
x  
 2
2
2
.
34



i
i
x
x
x
-24.2
-13.2
-1.2
18.8
19.8
10
21
33
53
54
585.64
174.24
1.44
353.44
392.04



5
1
171
i
i
x
2
.
34
5
171
5
5
1





i
i
x
x
7
.
376
4
8
.
1506
2


S
Calculating Formula for S2
:
1
1
2
2
2





n
x
n
x
S
n
i
i
* Simple
* More accurate

8. Note:
To calculate S2
we need:
· n = sample size
· The sum of the values
· The sum of the squared values
For the above example:
 
i
x
 
2
i
x
10 21 33 53 54
100 441 1089 2809 2916
i
x
2
i
x
 171
i
x
 7355
2
i
x
   7
.
376
4
8
.
1506
1
5
2
.
34
5
7355
2
2





S (unit)2
Standard Deviation:
· The standard deviation is another measure of variation.
· It is the square root of the variance.

9. (1) Population standard deviation is: (unit)
(2) Sample standard deviation is: (unit)
Example:
For the previous example, the sample standard deviation is
2

 
2
S
S 
41
.
19
7
.
376
2


 S
S (unit)
Coefficient of Variation (C.V.):
· The variance and the standard deviation are useful as measures
of variation of the values of a single variable for a single
population (or sample).
· If we want to compare the variation of two variables we cannot
use the variance or the standard deviation because:
1. The variables might have different units.
2. The variables might have different means.

10. · We need a measure of the relative variation that will not depend
on either the units or on how large the values are. This measure is the
coefficient of variation (C.V.) which is defined by:
%
100
*
.
x
S
V
C  (free of unit or unit
less)
Mean St.dev. C.V.
%
100
.
1
1
1
x
S
V
C 
%
100
.
2
2
2
x
S
V
C 
1
S
1
x
2
x 2
S
1st
data set
2nd
data set
· The relative variability in the 1st
data set is larger than the relative
variability in the 2nd
data set if C.V1
> C.V2
(and vice versa).

11. Example:
1st
data set: 66 kg, 4.5 kg
2nd
data set: 36 kg, 4.5 kg

1
x

2
S
%
8
.
6
%
100
*
66
5
.
4
. 1 

 V
C

2
x

2
S
%
5
.
12
%
100
*
36
5
.
4
. 2 

 V
C
Since , the relative variability in the 2nd
data set is larger
than the relative variability in the 1st
data set.
2
1 .
. V
C
V
C 
Notes: (Some properties of , S, and S2
:
Sample values are :
a and b are constants
x
n
x
x
x ,
,
, 2
1 

12. Sample Data Sample
mean
Sample
st.dev.
Sample
Variance
n
x
x
x ,
,
, 2
1 
n
ax
ax
ax ,
,
, 2
1 
b
x
b
x n 
 ,
,
,
1 
b
ax
b
ax n 
 ,
,
1 
x
x
a
b
x 
b
x
a 
S
S
a
S
S
a
2
S
2
2
S
a
2
S
2
2
S
a
Absolute value:
 0
0



 a
if
a
a
if
a
a

13. Sample Sample
mean
Sample
St..dev.
Sample
Variance
C. V.
1,3,5 3 2 4 66.7%
(1)
(2)
(3)
-2, -6, -10
11, 13, 15
8, 4, 0
-6
13
4
4
2
4
16
4
16
66.7%
15.4%
100%
Example:
Data (1) (a = 2)
(2) (b = 10)
(3) (a = 2, b = 10)
3
2
1 2
,
2
,
2 x
x
x 


10
x
,
10
x
,
10
x 3
2
1 


10
x
2
,
10
x
2
,
10
x
2 3
2
1 






14. Can C. V. exceed 100%?
Data: 10,1,1,0
Mean=3
Variance=22
STDEV=4.6904
C. V.=156.3%