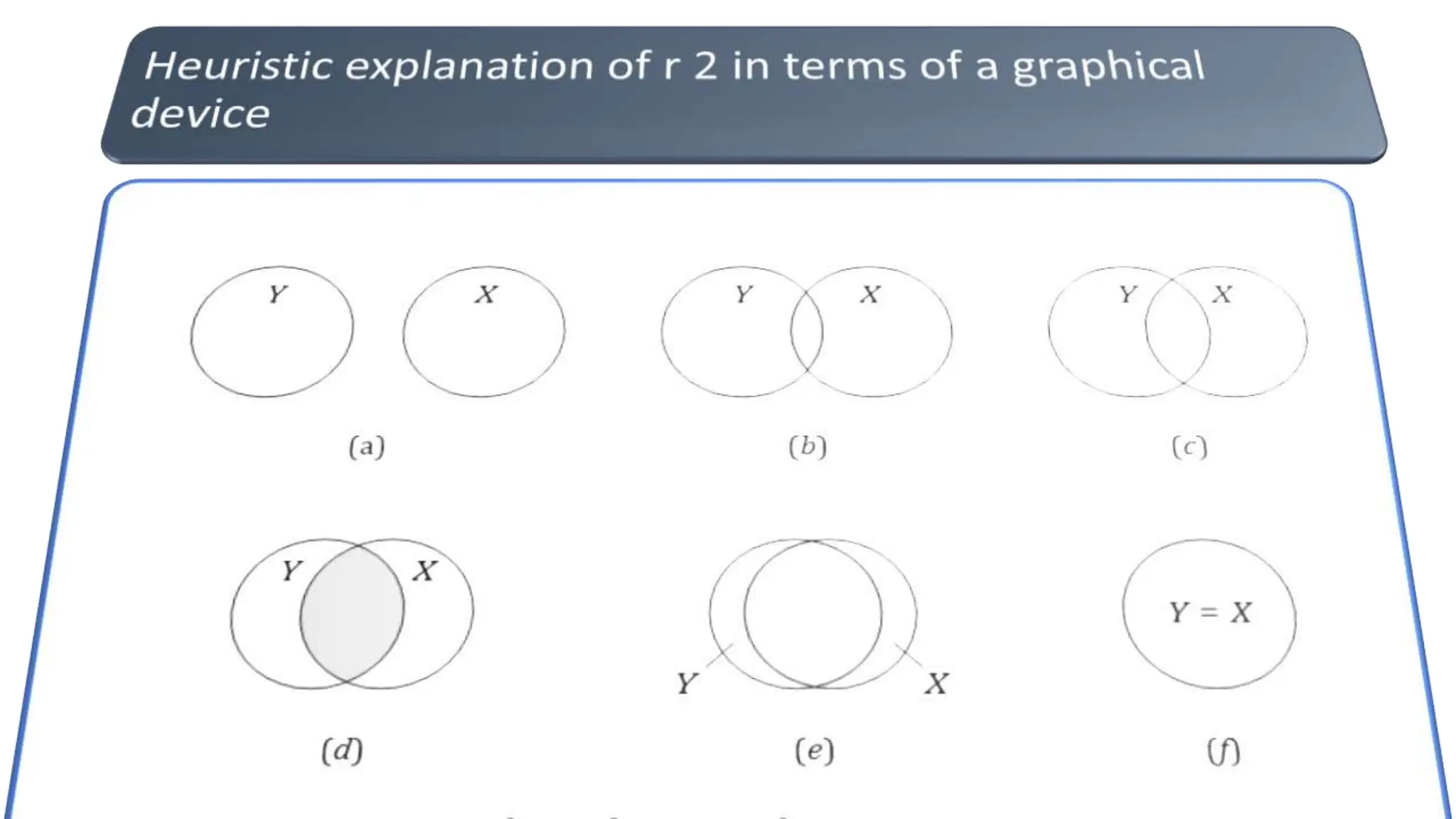
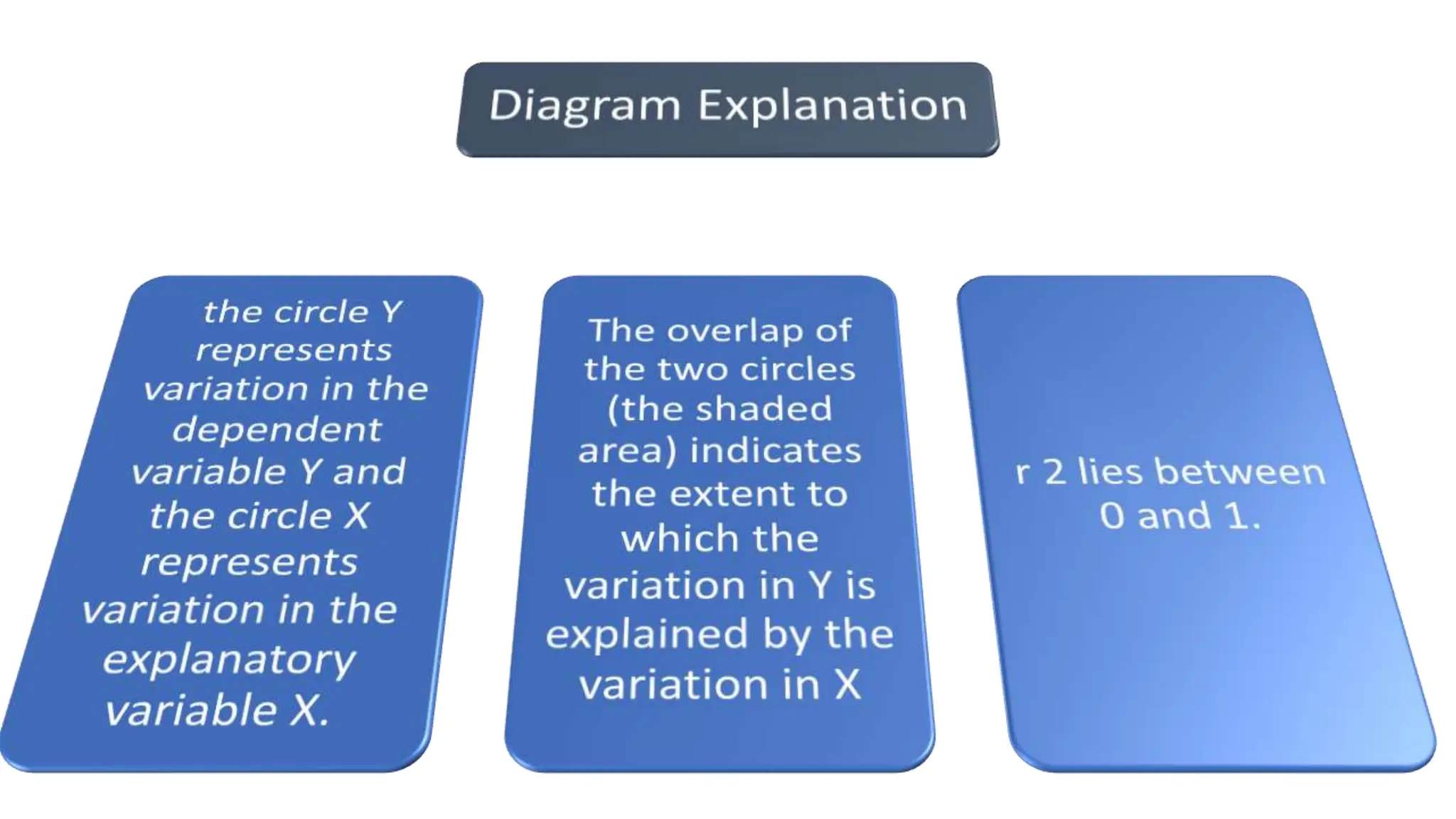
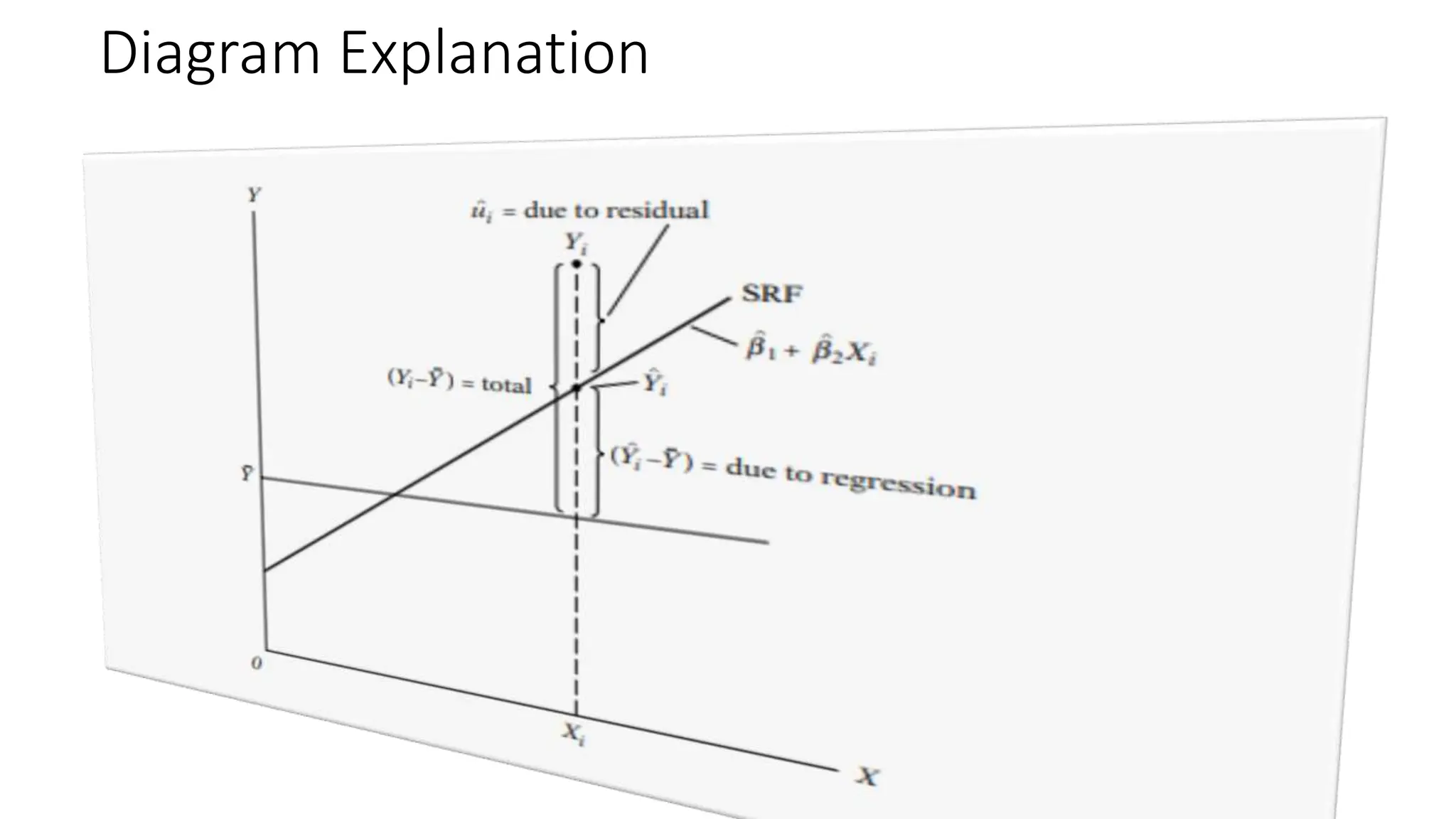
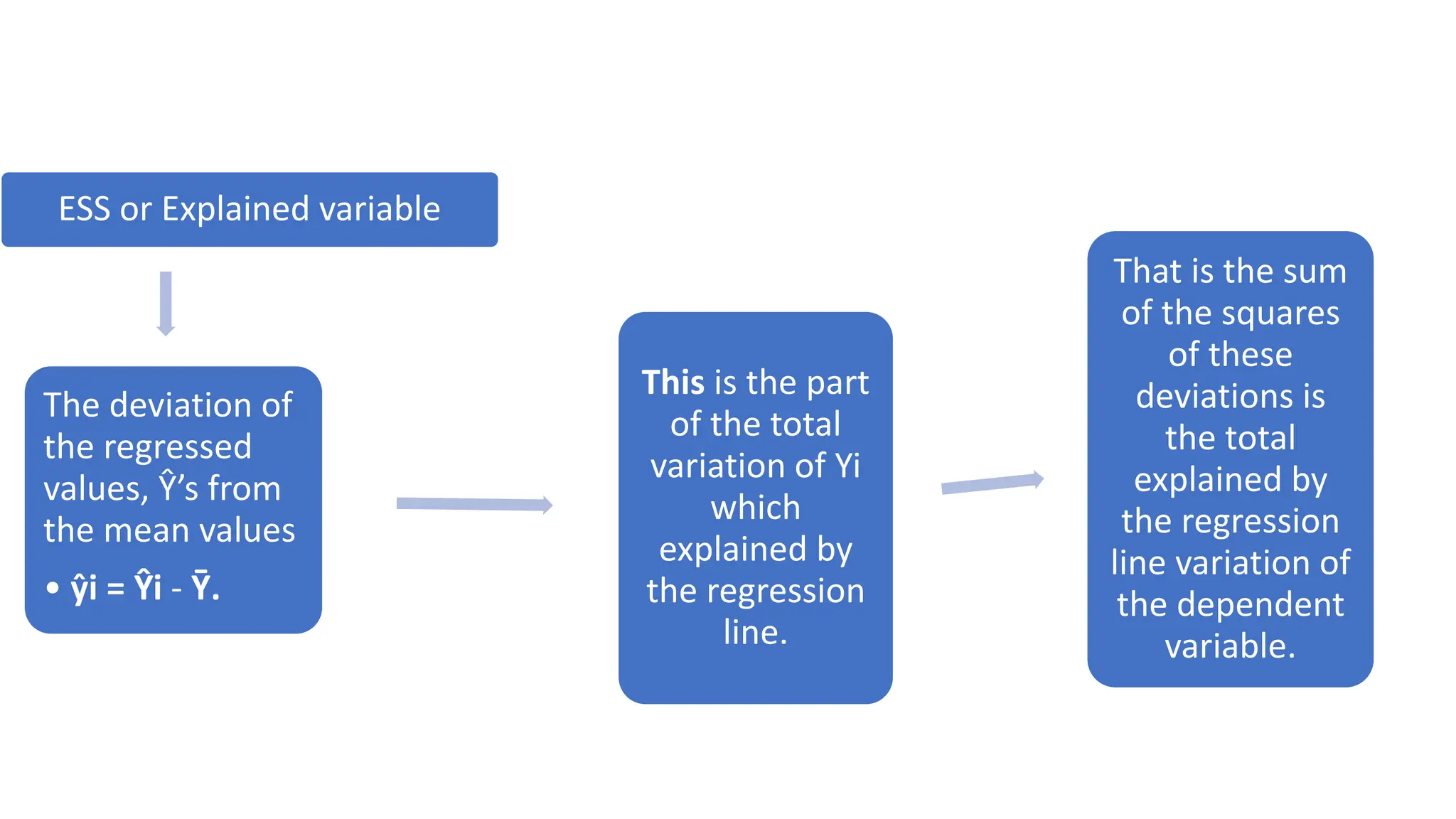
The document discusses the concept of goodness of fit in regression analysis, emphasizing how well the sample regression line fits the data. It explains that the goodness of fit is measured by the square of the correlation coefficient (R²), indicating the percentage of the total variation in the dependent variable that can be explained by the independent variable. It also delineates the total variation into explained and unexplained components, detailing how the variations are calculated.

1. Goodness of Fit

2. we shall find out how “well” the
sample regression line fits the
data
We need to know how goodness
is the fit of this line to the sample
observations of Y and X.
If the closer the observation to
the line, the better the goodness
of fit. That is the explanation of
the variations of Y by the changes
in the explanatory variables.

5. Meaning
The measurement of the
goodness of fits is the square
of the correlation coefficients
r Square
which means that the percentage
of the total variation of dependent
variable that can be explained by
the independent variable X.

6. Diagram Explanation

7. Deviation of the observed value of Y into two
component
• Firstly, it is explained by the regression line variation
• Secondly, the unexplained variation.
• That is

8. TSS or Total variation
• The total variation of the dependent variable by comparing each
value of Y to the mean Ȳ and adding all the resulting deviations.
• That is

9. ESS or Explained variable
The deviation of
the regressed
values, Ŷ’s from
the mean values
• ŷi = Ŷi - Ȳ.
This is the part
of the total
variation of Yi
which
explained by
the regression
line.
That is the sum
of the squares
of these
deviations is
the total
explained by
the regression
line variation of
the dependent
variable.

10. RSS or Unexplained variable
• This is a part of the variation of the dependent variable which is not
explained by the regression line.
• Thus the sum of the squared residuals gives the total unexplained
variation of the dependent variable Y around its mean.
• That is