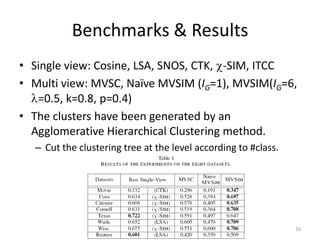
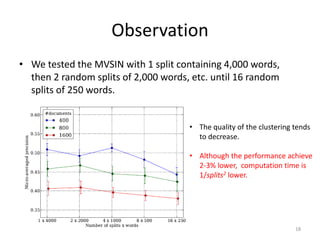
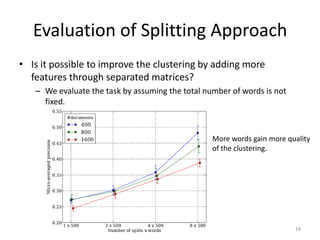
This document summarizes a research paper on co-clustering multi-view datasets using a parallelizable approach called MVSIM. MVSIM computes co-similarity matrices for related objects across multiple views or relation matrices. It creates a learning network matching the relational structure and aggregates the similarity matrices using a damping factor. Experiments show MVSIM outperforms single-view and other multi-view clustering methods on document and newsgroup datasets, and its performance decreases slightly but computation time reduces significantly when the data is split across more views.

1. Co-clustering of Multi-View Datasets:
a Parallelizable Approach
Authors/ Gilles Bisson and Clement Grimal
Affiliation/ University Joseph Forier, France
Source/ International Conference on Data Mining 2012
Presenter/ Allen
1

2. Outline
•
•
•
•
•
•
Introduction
Multi-View Learning
The -SIM algorithm
The MVSIM architecture
Experiments
Conclusion
2

3. Introduction
• Co-clustering have been proposed to observe the intensity
of relation between two objects.
• However, datasets involving more than two types of
interacting objects are also frequent.
– In addition to analyze users’ relation in a social network, the
relations between documents and users are also needed to be
analyzed.
• A simple way is to process such datasets into many
matrices and co-cluster them separately.
– Interactions between objects in difference matrices are not
considered.
3

4. Introduction (Cont.)
• Multi-view clustering task, handle the views
together, was proposed to solve this problem.
•
-SIM is a co-clustering algorithm, which builds
similarity matrices rather than produce co-cluster
results.
– It is flexible to combine different views together.
– It can be easily inject priori knowledge into initialized
similarity matrix.
– It’s possible to transfer the similarities form one view
to the others.
4

5. Multi-view learning
• Multi-view learning became highly popular
with the seminal work of co-training, which
trained two algorithms on two different views.
• Several extensions of classical clustering
methods have been proposed to deal with
multi-view data.
– Multi-view K-means (MVKM)
– Multi-view EM
5

6. Multi-view learning
• Multi-view clustering aims at combining multiple
results into one.
– Occurrence
• Fred et al. produced a meta-similarity matrix based on how many
times objects appear in the same cluster.
– Clustering ensemble selection problem
• Li et al. built a weighted consensus clustering methods to select
the best clustering among multi views.
• Azimi et al. adapts their selection strategy according to stability of
clustering.
– Fusion manner
• Combining multiple similarity matrices to perform a given learning
task.
– Linked Matrix Factorization, fuzzy clustering
6

7. Notations
• Type of objects
– Let N be the number of objects in the dataset. (i.e.
users, documents, words, etc.)
• Ti is an object. i 1…N
• For simplify, object Ti has ni instances.
– Relation matrices
• Let M be the number of relations between objects.
ni nj is the relation matrix between objects T and T .
• Rij
i
j
– Similarity matrices
ni ni is the square and symmetrical
• Similarity matrix Si
matrix of Ti, where the values must be in [0,1].
7

8. The -SIM algorithm [SDM’10]
• Let R12 is a [documents/words] matrix and that
the task is to compute the similarity matrix S1
(documents) and S2 (words).
• The idea of -SIM is to capture the duality
between documents and words.
• This is achieved by simultaneously calculating
document-document similarities based on words,
and word-word similarities based on documents.
8

9. The -SIM algorithm (cont.)
• The similarity matrix S1 between documents is
evaluated in two steps:
– The k parameter is similar to one used in
Minkowski distance.
The Minkowski distance of order p between two points
is defined as:
9

10. The -SIM algorithm (cont.)
• Parameter p: the percentage of
the smallest similarity needed to
be pruned.
• If k=1, It=1 and p=0, -SIM is
equivalent to cosine similarity.
R12
word1
word2
word3
doc1
2
1
0
doc2
1
2
3
doc3
0
1
2
S1
doc1
doc2
doc3
doc1
5
4
1
doc2
4
14
8
doc3
1
8
5
10

11. The MVSIM architecture
• This architecture deal with
datasets having multiple
relation matrices (or views).
• The goal:
– Compute a co-similarity
matrix Si for object Ti which
appear in different views.
• The idea:
The input: Si, Sj, Ri,j, i,j 1…N
The output: Si(i,j), Sj(i,j), Rij, i,j 1…N
The aggregation function: i, j
– Create a learning network
isomorphic to the relational
structure of the datasets.
11

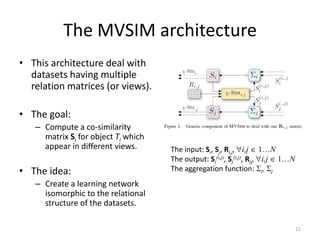
12. Aggregation Function
• Functions
i
have two important roles:
– Aggregate the multiple similarity matrices
produced by -SIM.
• F(Si(i,1), Si(i,2),..): merging function combining matrices.
– Ensure the convergence
• Use damping factor
[0,1] to balance the function
i
12

13. The MVSIM algorithm
• IG: the number of iterations for MVSIM.
• For simplify, k, p and It are set to the same.
13

14. Complexity and Parallelization
• Complexity
– MVSIM is related to -SIM.
• Time complexity: O(nm2+n2m)
• Parallelization
n m, it will be spilt into h
– For one relation matrix R12
small matrices. (n: # documents; m: # words)
• If m is huge, R12 can be divided into h small matrices
n (m/h).
R’
• Using a distributed version on h cores.
– Time complexity is decreased to O(1/h2(nm2)+1/h(n2m))
– Memory storage is decreased to 1/h.
14

15. Evaluation of multi-view approaches
• Evaluating the correlation between the learned
and known clusters in the confusion matrix.
– Measurement: micro-averaged precision
• Datasets (Ground truth: document class)
– IMDB
– CiteSeer
– 4 universities datasets: Cornell, Texas, Washington and
Wisconsin
– Reuters RCV1/RCV2
15

16. Benchmarks & Results
• Single view: Cosine, LSA, SNOS, CTK, -SIM, ITCC
• Multi view: MVSC, Naïve MVSIM (IG=1), MVSIM(IG=6,
=0.5, k=0.8, p=0.4)
• The clusters have been generated by an
Agglomerative Hierarchical Clustering method.
– Cut the clustering tree at the level according to #class.
16

17. Evaluation of Splitting Approach
• Dataset
– NG20: 20,000 newsgroup
– Ground truth: 10 categories
• How is the quality of the clustering influenced,
when #splits increases with a total #features
kept constant?
17

18. Observation
• We tested the MVSIN with 1 split containing 4,000 words,
then 2 random splits of 2,000 words, etc. until 16 random
splits of 250 words.
• The quality of the clustering tends
to decrease.
• Although the performance achieve
2-3% lower, computation time is
1/splits2 lower.
18

19. Evaluation of Splitting Approach
• Is it possible to improve the clustering by adding more
features through separated matrices?
– We evaluate the task by assuming the total number of words is not
fixed.
More words gain more quality
of the clustering.
19

20. Conclusion
• The MVSIM architecture deal with the problem of
learning co-similarities from a collection of
matrices describing interrelated types of objects.
• It provides interesting properties in terms of
convergence and scalability, and allows a
straightforward parallelization of the process.
• The experiments demonstrate that this method
outperform both single-view and multi-view
approaches.
20