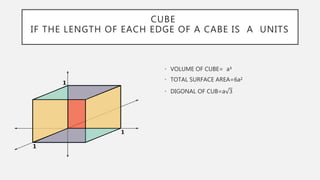
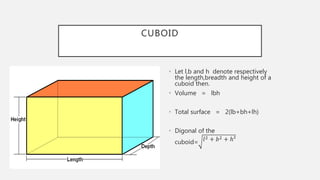
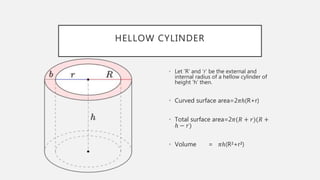
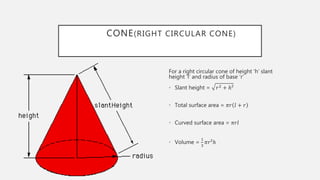
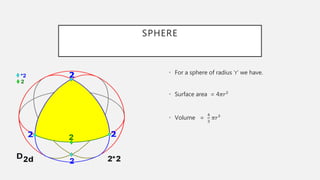
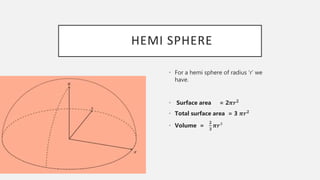
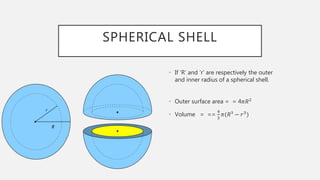
The document provides formulas for calculating the surface areas and volumes of basic 3D shapes including cubes, cuboids, cylinders, cones, spheres, hemispheres, and spherical shells. It lists the key measurements needed such as length, width, height, radius, and slant height. Formulas given include calculating the volume, total surface area, curved surface area, and diagonals or slant heights for each shape.

1. BASIC FORMULA
SURFACE AREAS AND VOLUME
PRESENTED BY RAKESH VERMA

2. INDEX
• CUBE
• CUBOID
• RIGHT CIRCULAR CYLINDER
• CONE
• SPHERE

3. CUBE
IF THE LENGTH OF EACH EDGE OF A CABE IS A UNITS
• VOLUME OF CUBE= a³
• TOTAL SURFACE AREA=6a²
• DIGONAL OF CUB=a 3

4. CUBOID
• Let l,b and h denote respectively
the length,breadth and height of a
cuboid then.
• Volume = lbh
• Total surface = 2(lb+bh+lh)
• Digonal of the
cuboid= 𝑙2 + 𝑏2 + ℎ²

5. CYLINDER(RIGHT CIRCULAR CYLINDER)
• For base radius ‘r’ and height ‘h’ then.
• Curved surface area=2𝜋𝑟ℎ
• Total surface area=2𝜋𝑟(h+r)
• Volume= 𝜋𝑟²ℎ

6. HELLOW CYLINDER
• Let ‘R’ and ‘r’ be the external and
internal radius of a hellow cylinder of
height ‘h’ then.
• Curved surface area=2𝜋ℎ(R+r)
• Total surface area=2𝜋(𝑅 + 𝑟)(𝑅 +
ℎ − 𝑟)
• Volume = 𝜋ℎ(R²+r²)

7. CONE(RIGHT CIRCULAR CONE)
For a right circular cone of height ‘h’ slant
height ‘l’ and radius of base ‘r’
• Slant height = 𝑟2 + ℎ²
• Total surface area = 𝜋𝑟 𝑙 + 𝑟
• Curved surface area = 𝜋𝑟𝑙
• Volume =
1
3
𝜋𝑟²ℎ

8. CONE(FRUSTUM OF CONE)
• Slant height = ℎ2 + (𝑅 − 𝑟)²
• Total surface area = 𝜋𝑙 𝑅 + 𝑟 +
𝜋(𝑅 + 𝑟)
• Volume =
1
3
𝜋ℎ (R+Rr+r²)
• Lateral surface area = 𝜋𝑙 (𝑅 + 𝑟)

9. SPHERE
• For a sphere of radius ‘r’ we have.
• Surface area = 4𝜋𝑟²
• Volume =
4
3
𝜋𝑟³

10. HEMI SPHERE
• For a hemi sphere of radius ‘r’ we
have.
• Surface area = 2𝝅𝒓 𝟐
• Total surface area = 3 𝝅𝒓 𝟐
• Volume =
𝟐
𝟑
𝝅𝒓³

11. END

12. SPHERICAL SHELL
• If ‘R’ and ‘r’ are respectively the outer
and inner radius of a spherical shell.
• Outer surface area = = 4𝜋𝑅2
• Volume = ==
4
3
𝜋(𝑅³ − 𝑟3)