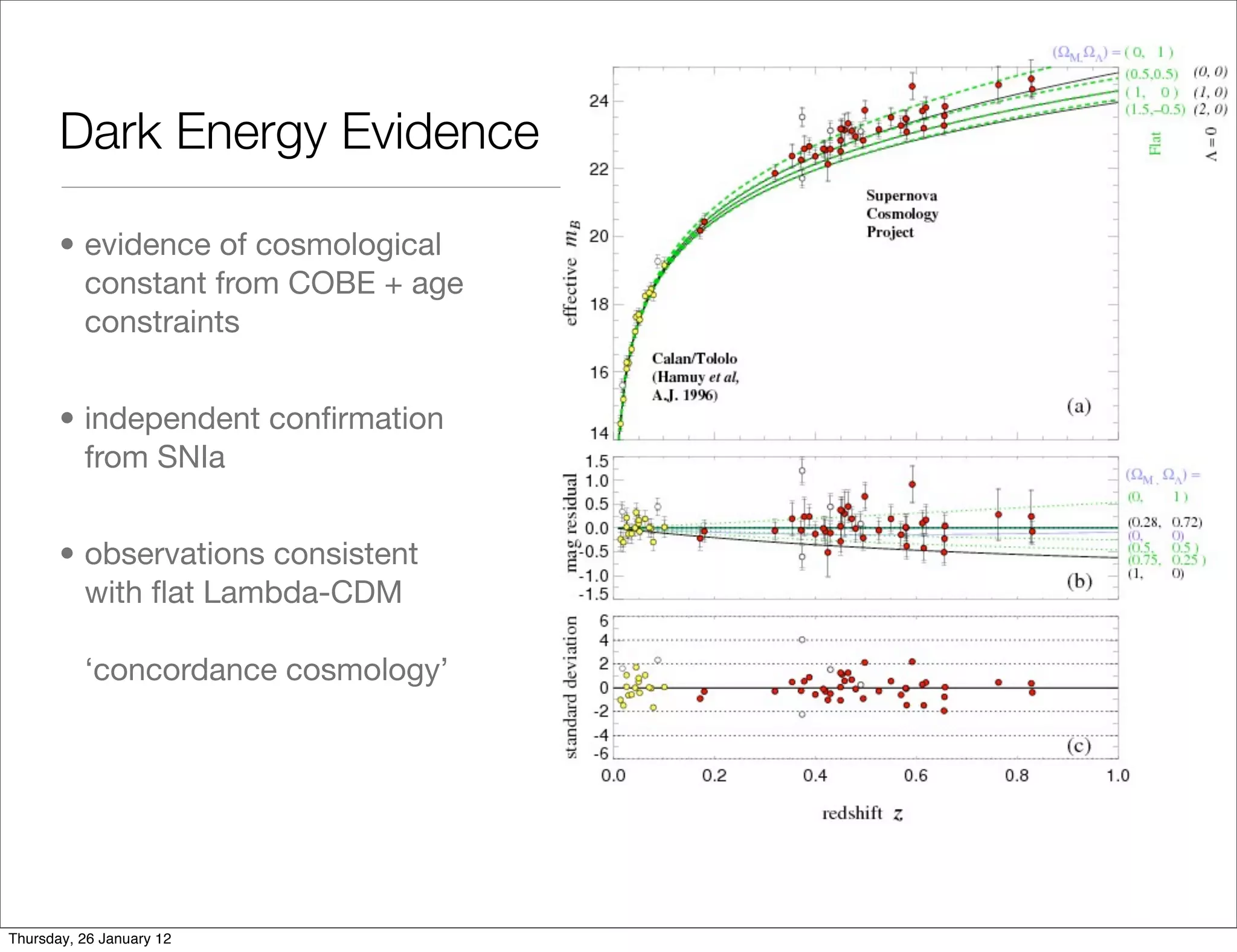
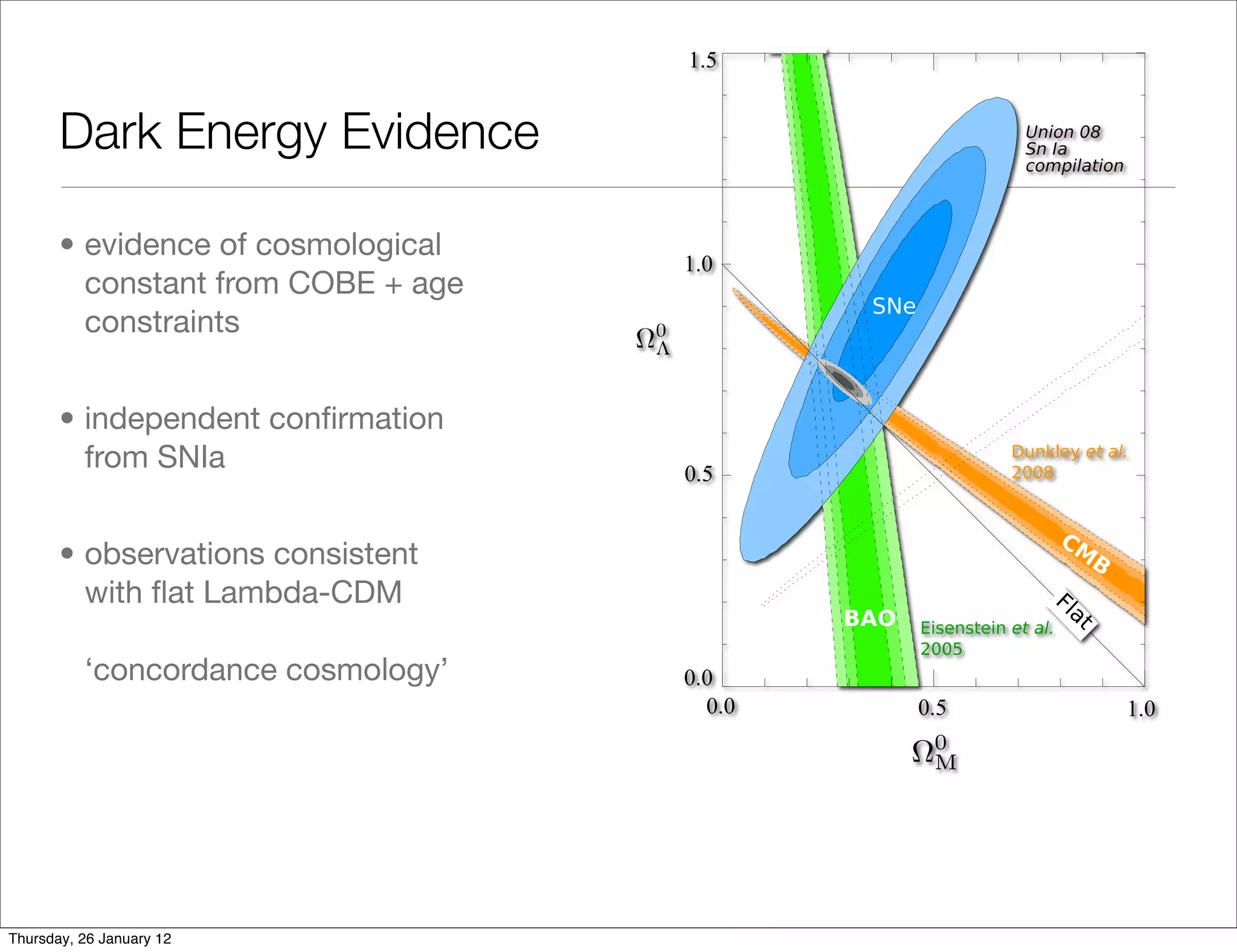
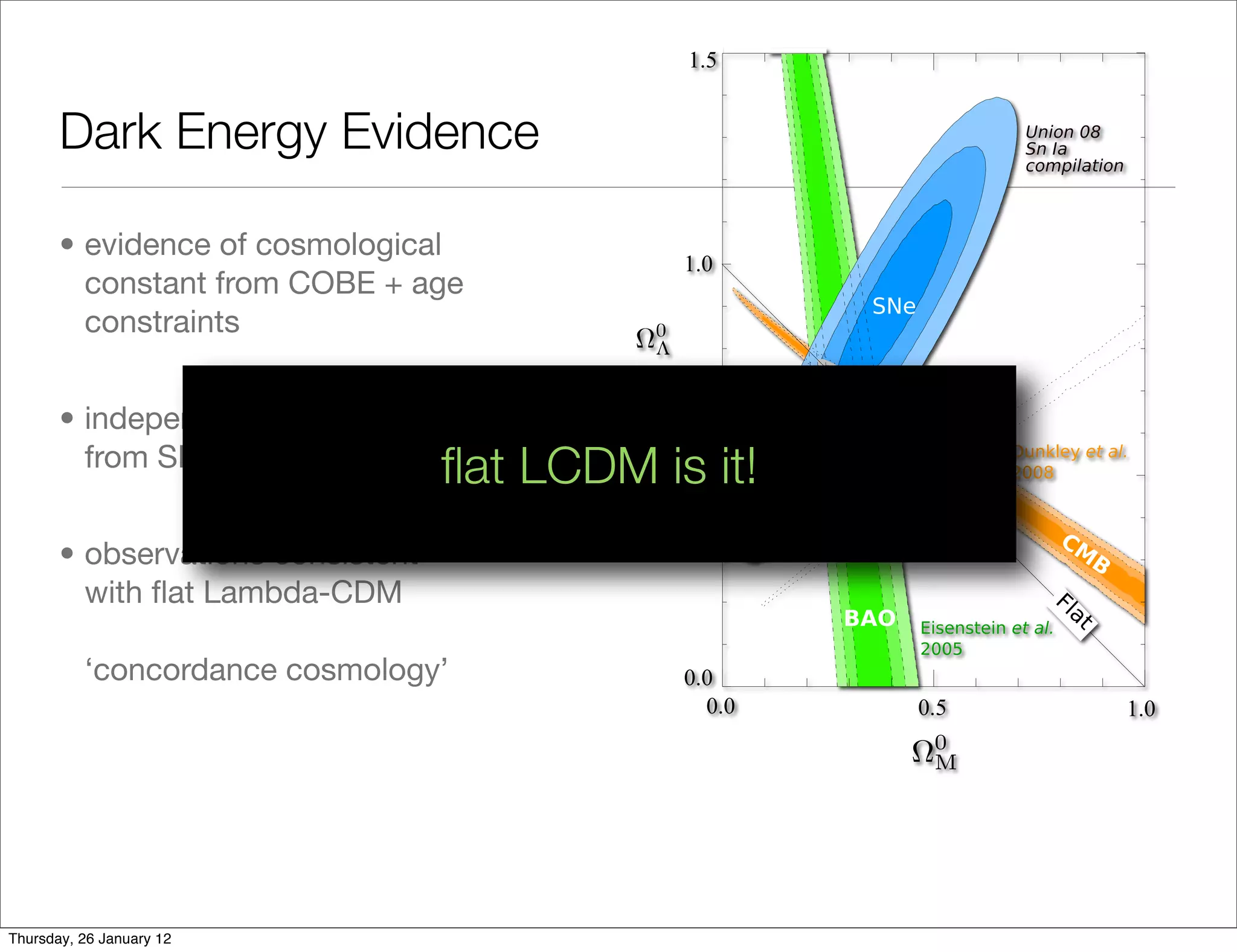
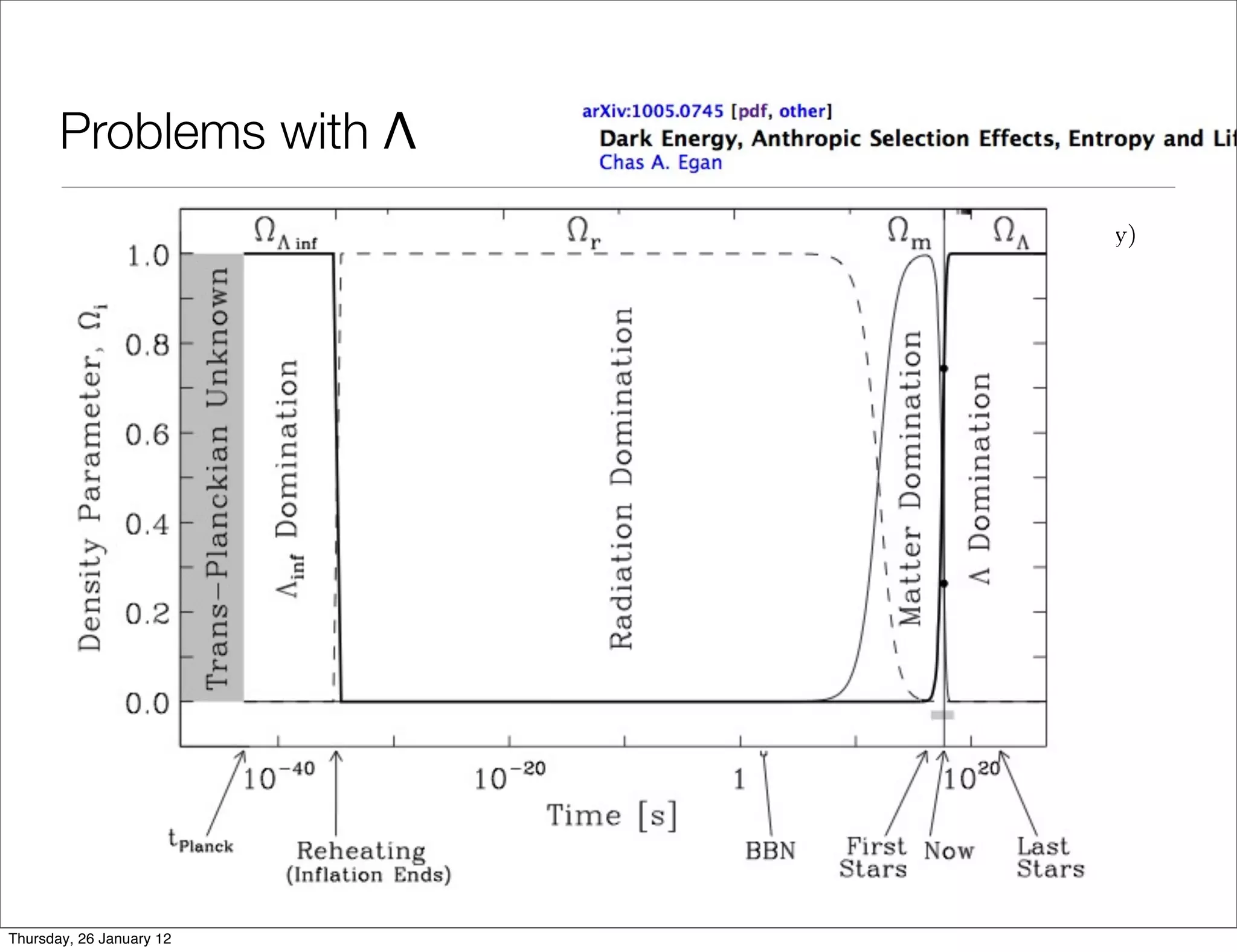
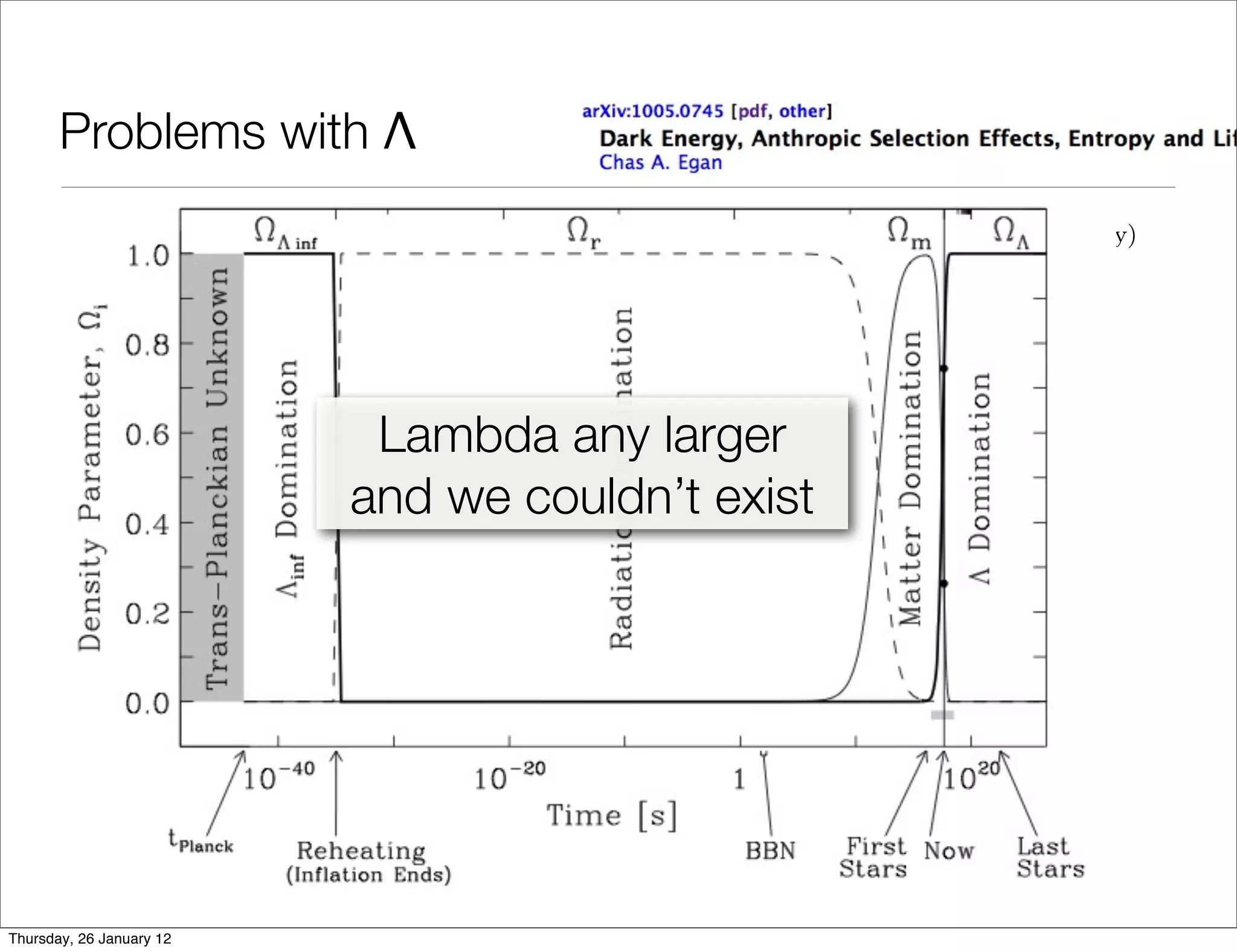
The document discusses evidence for dark energy and the Lambda Cold Dark Matter (Lambda-CDM) model of cosmology. It notes that:
1) Evidence from COBE and age constraints provides evidence for a cosmological constant.
2) Type Ia supernovae provide independent confirmation of dark energy.
3) Observations are consistent with a flat Lambda-CDM model, known as the "concordance cosmology".
However, the cosmological constant poses theoretical problems, such as a discrepancy of 30 orders of magnitude between observed and predicted vacuum energy densities. Alternatives to Lambda-CDM that could still be consistent with observations are also discussed.








![z jump =0.085 ; ∆CENTRE =-0.48
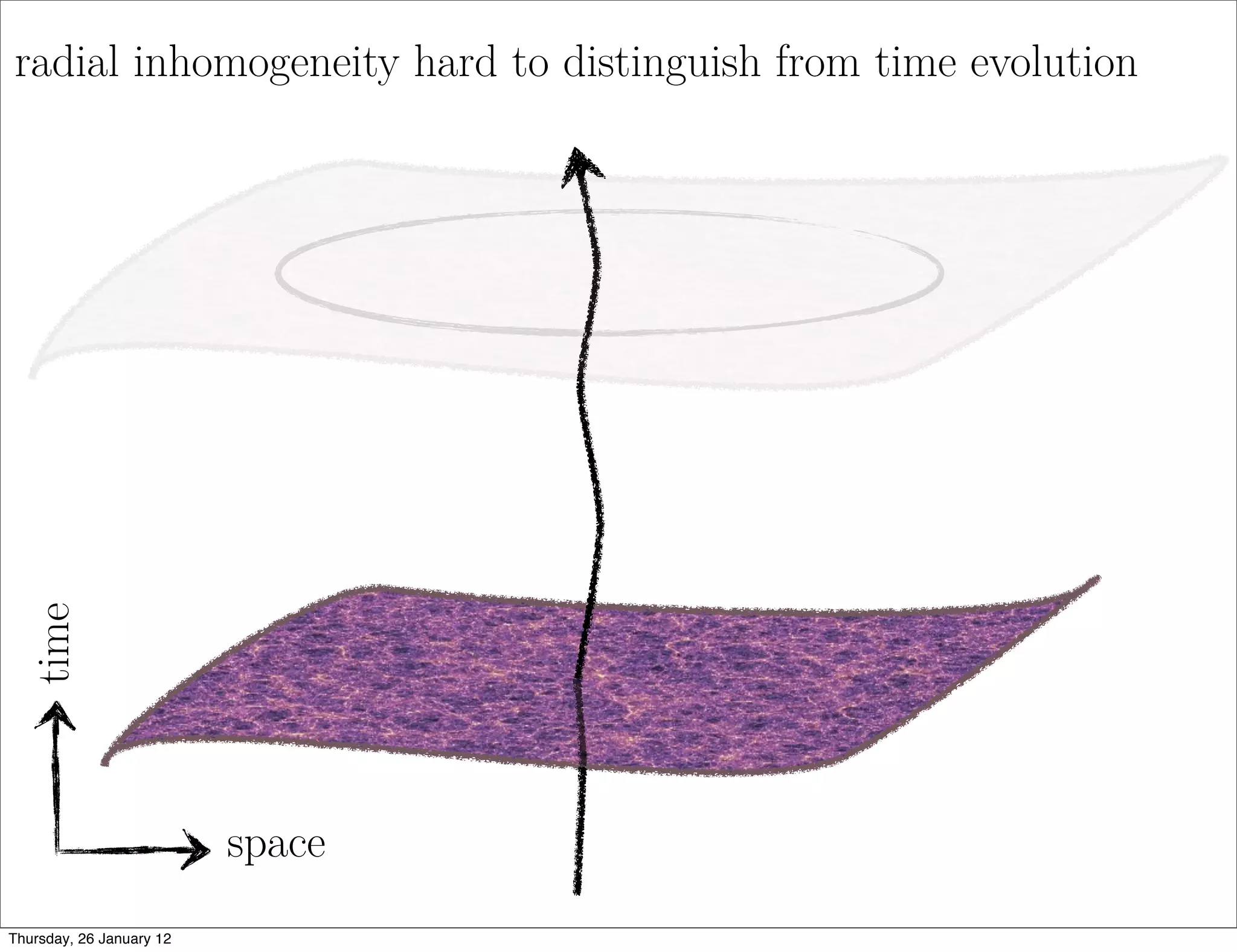
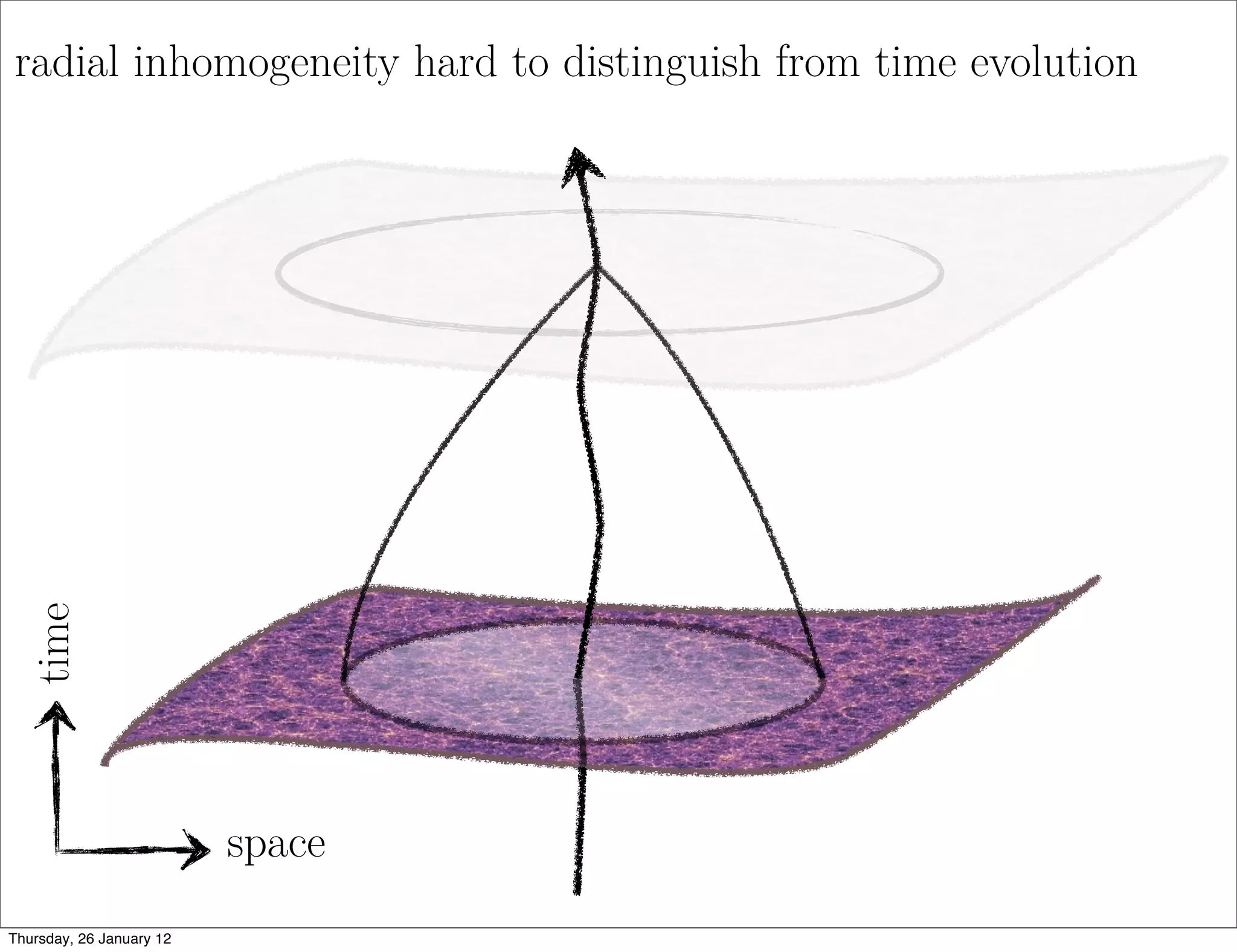
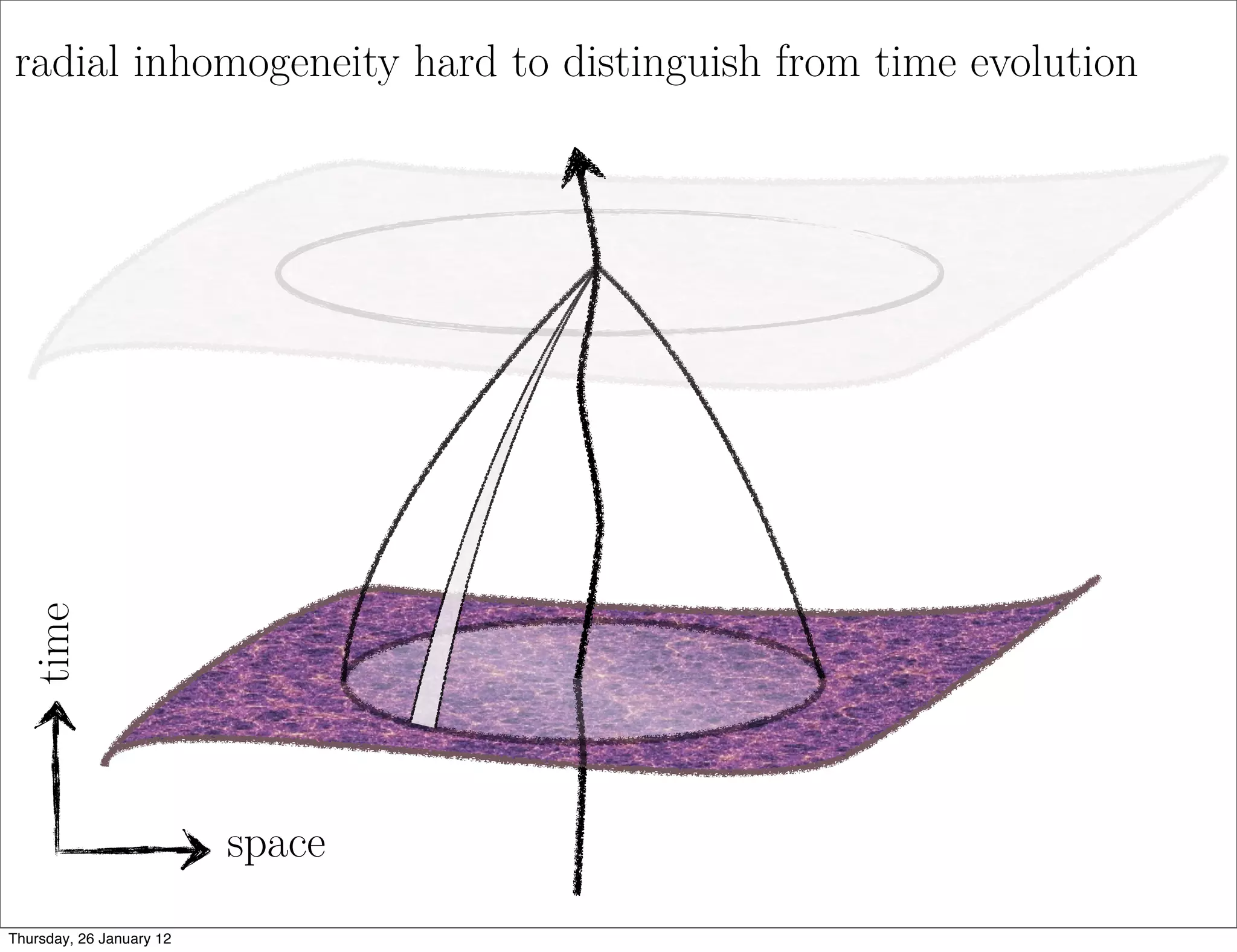
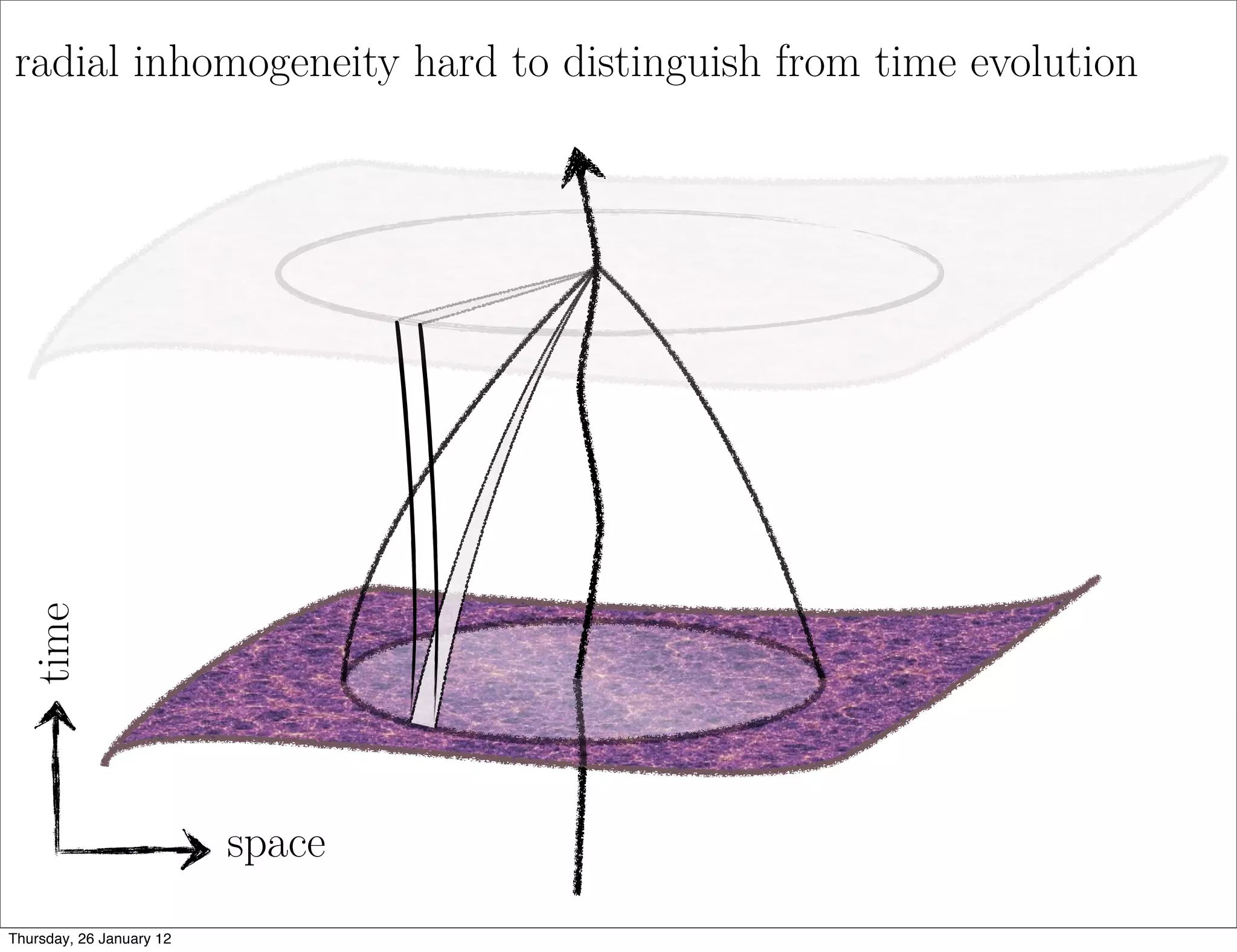
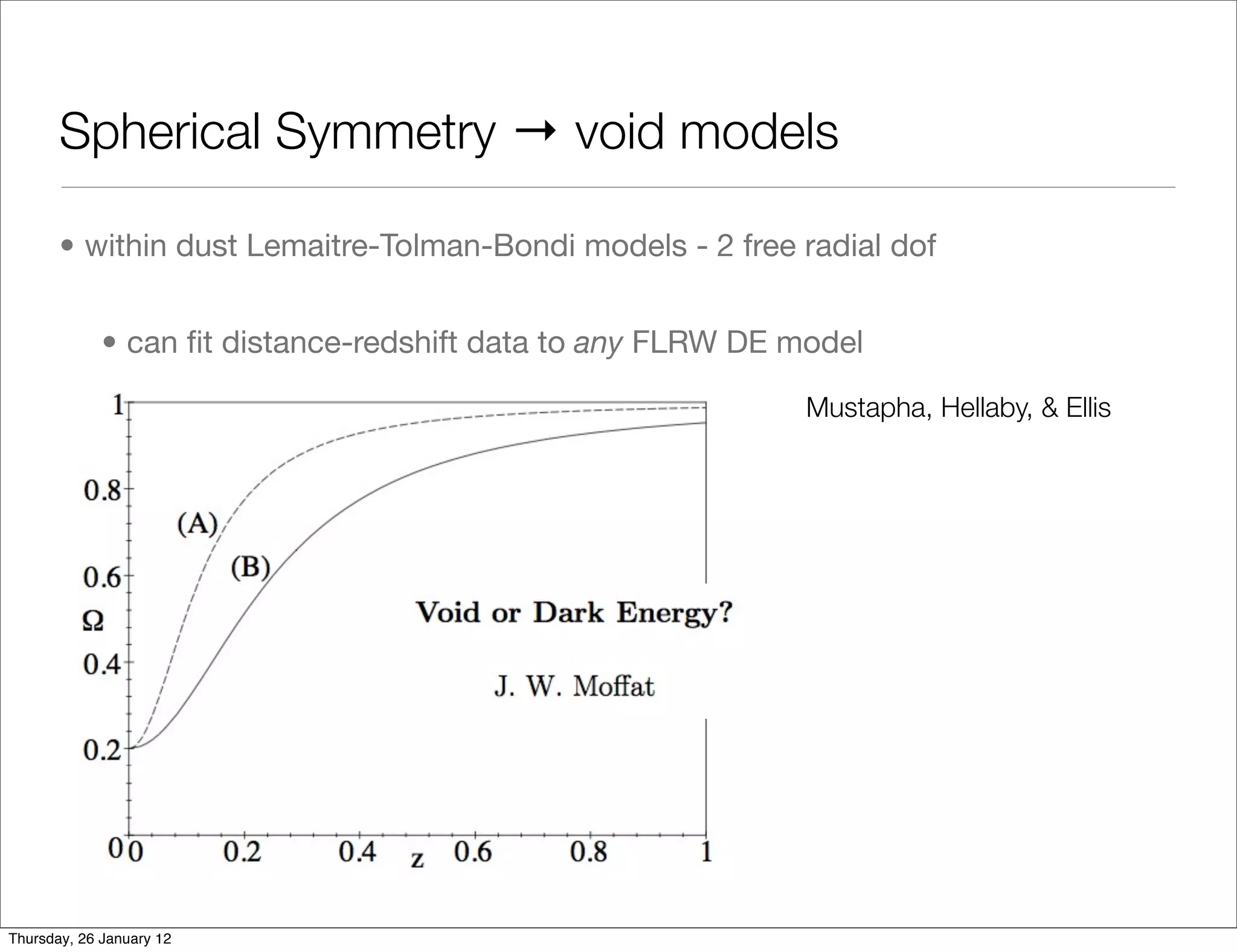
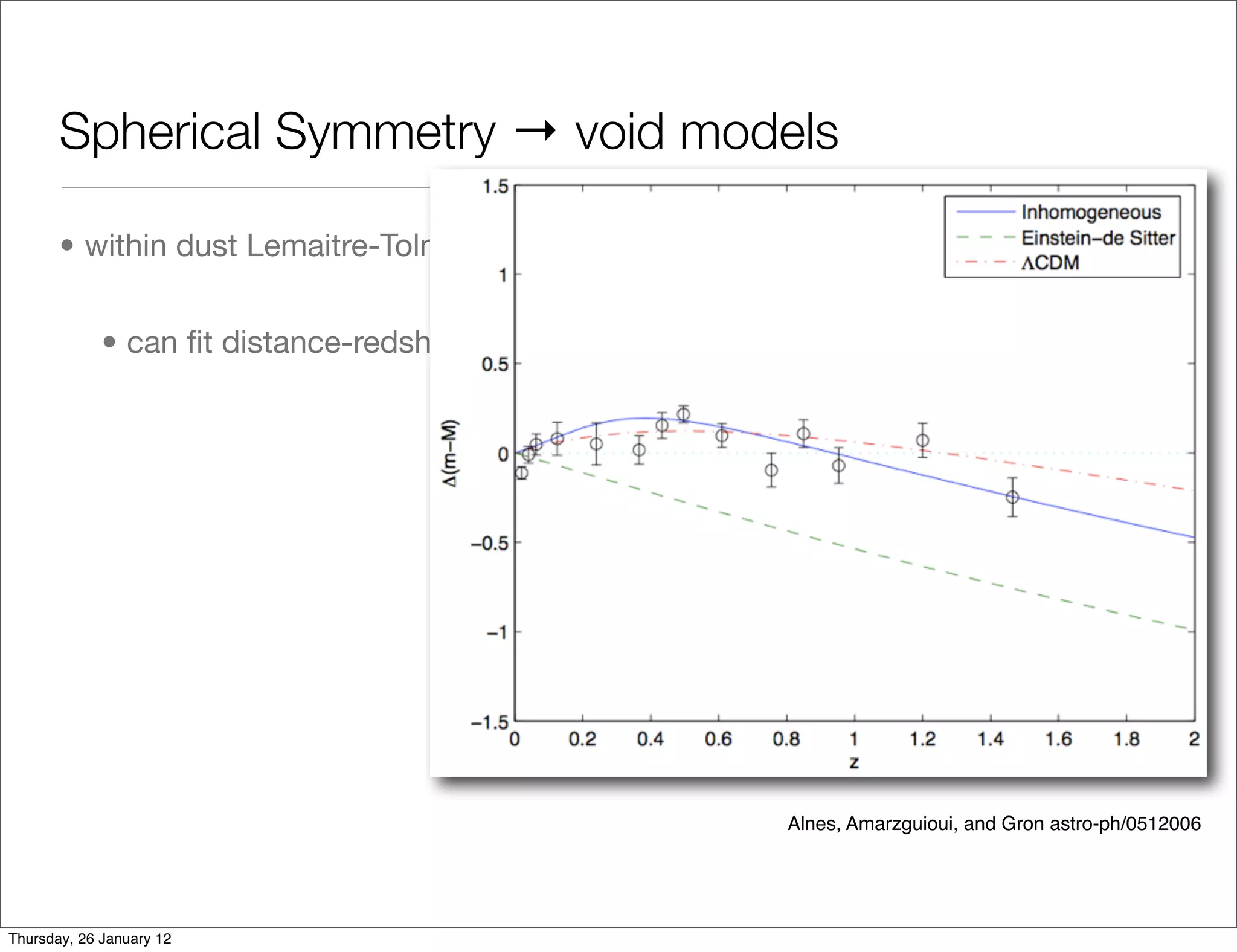
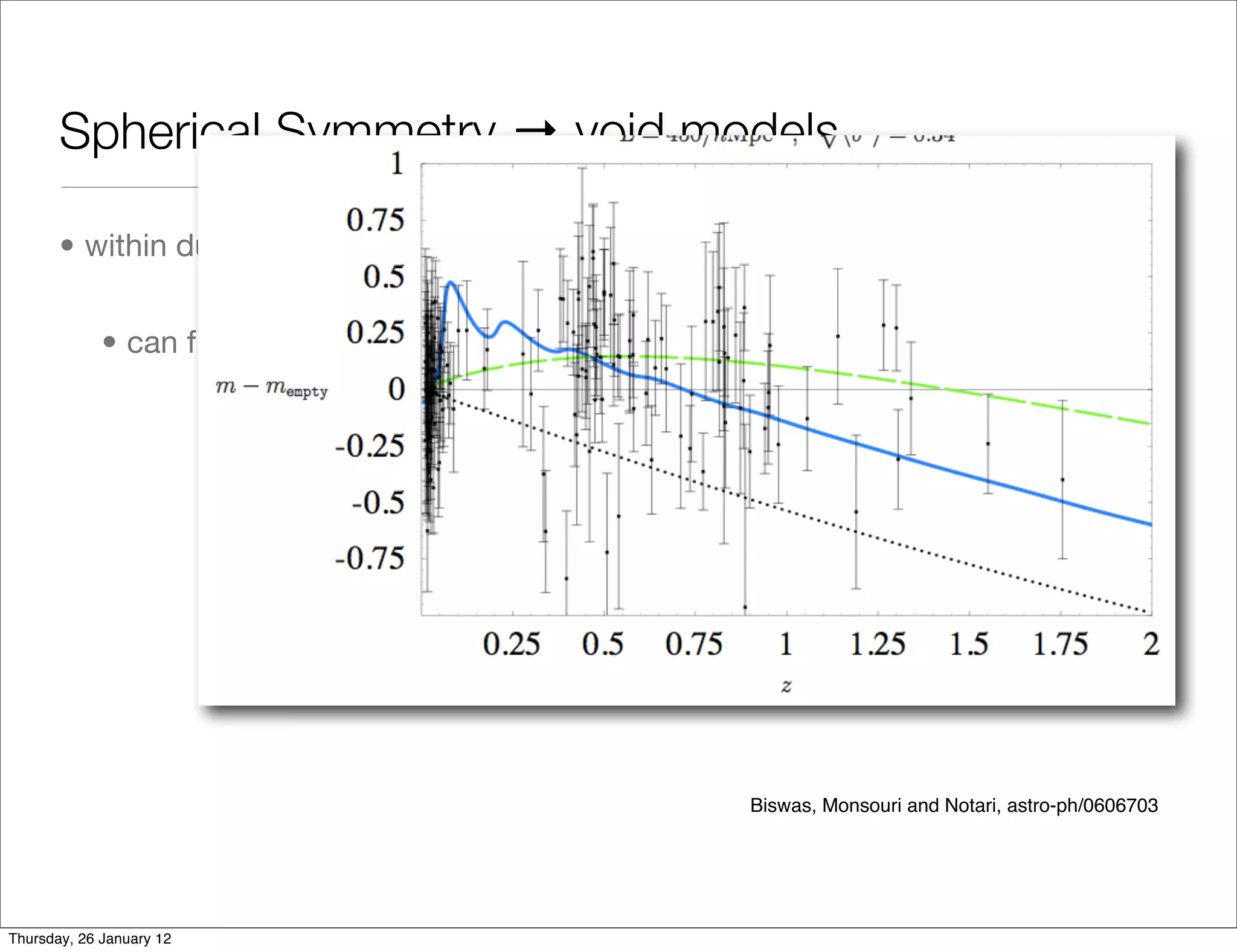
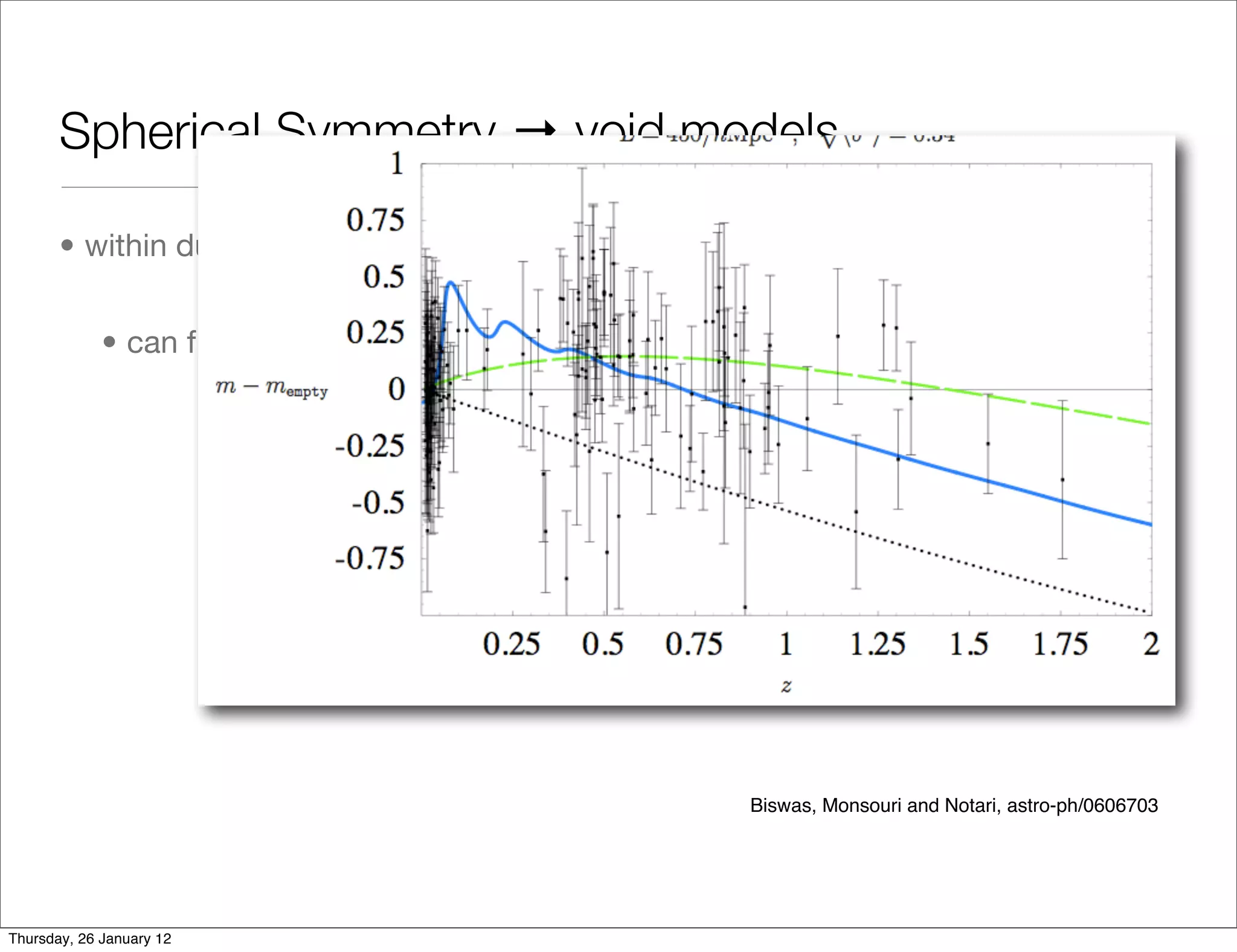
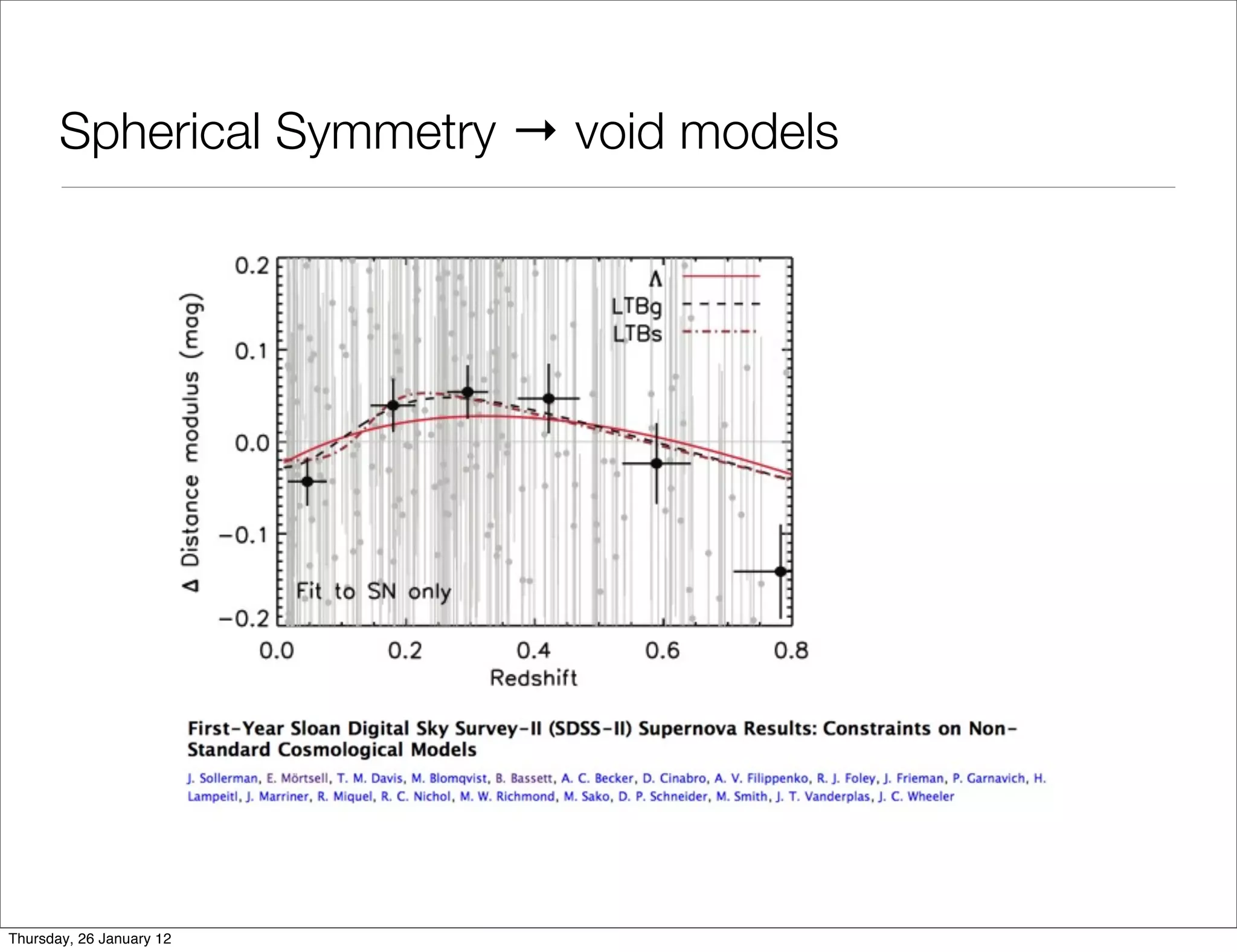
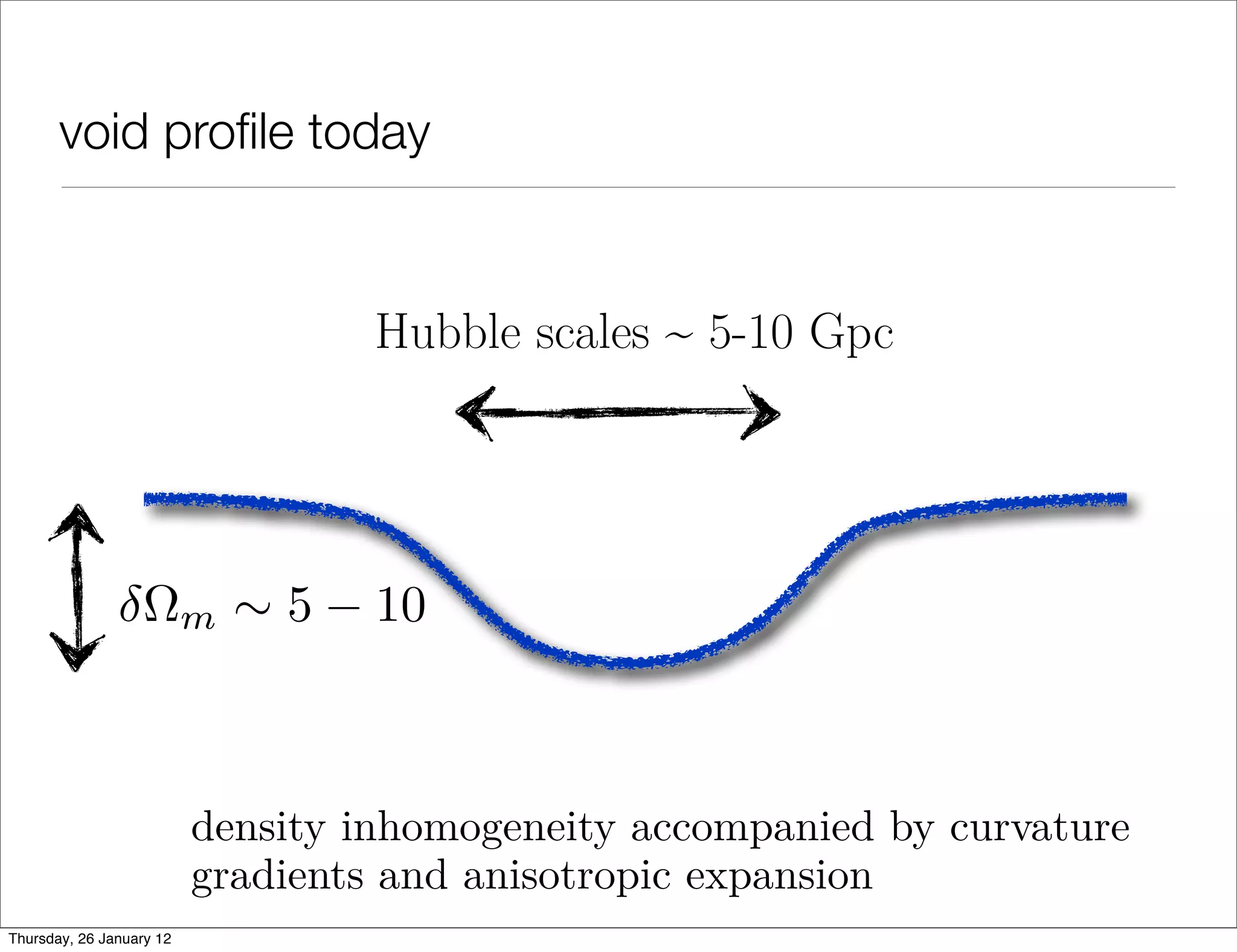
Spherical Symmetry → void models
0.75
0.5
0.25
• within dust Lemaitre-Tolman-Bondi models - 2 free radial dof
0
m
-0.25
• can fit distance-redshift data to any FLRW DE model
-0.5
-0.75 Mustapha, Hellaby, & Ellis
-1
0 0.25 0.5 0.75 1 1.25 1.5 1.75
z
1
0.75
0.5
0.25
∆Ρ
0
Ρ
-0.25
-0.5
-0.75
Biswas, Monsouri and Notari, astro-ph/0606703
0 0.02 0.04 0.06 0.08
z
FIG. 3: In the upper plot we show a fit of the Supernovae data (Riess et al. [28]) with an LTB model which has χ2 =
d.o.f. are 181). The inhomogeneous patch extends up to z 0.085 and the underdensity in the center is δCENTRE
Thursday, 26 January 12 We have shown ∆m ≡ m − mempty : the magnitude (m ≡ 5Log10 DL ) minus the magnitude of an empty open FLRW](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-23-2048.jpg)



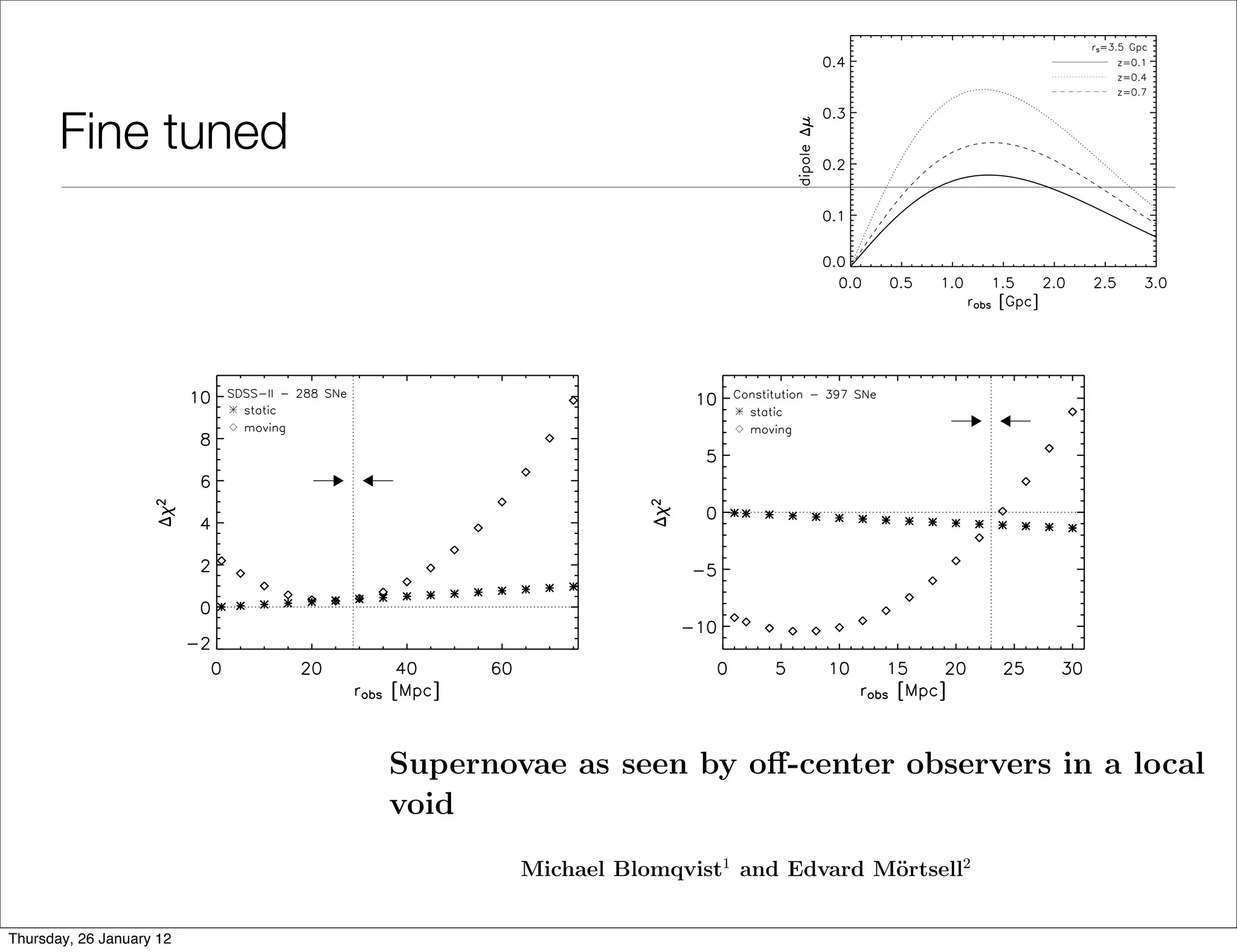




![Isn’t this a bit silly?
• Yes
• But:
• we should be able to rule all void models out observationally - tests CP
• helps make data ‘cosmology independent’ (eg, compare SNIa vs BAO)
• provides alternative probe of coincidence problem which can be tested
• unusual DE interpretation without LCDM as fixed point - only DE model
with known physics at late times
• can we construct a void which fits all observations? [v fine-tuned?]
Thursday, 26 January 12](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-38-2048.jpg)
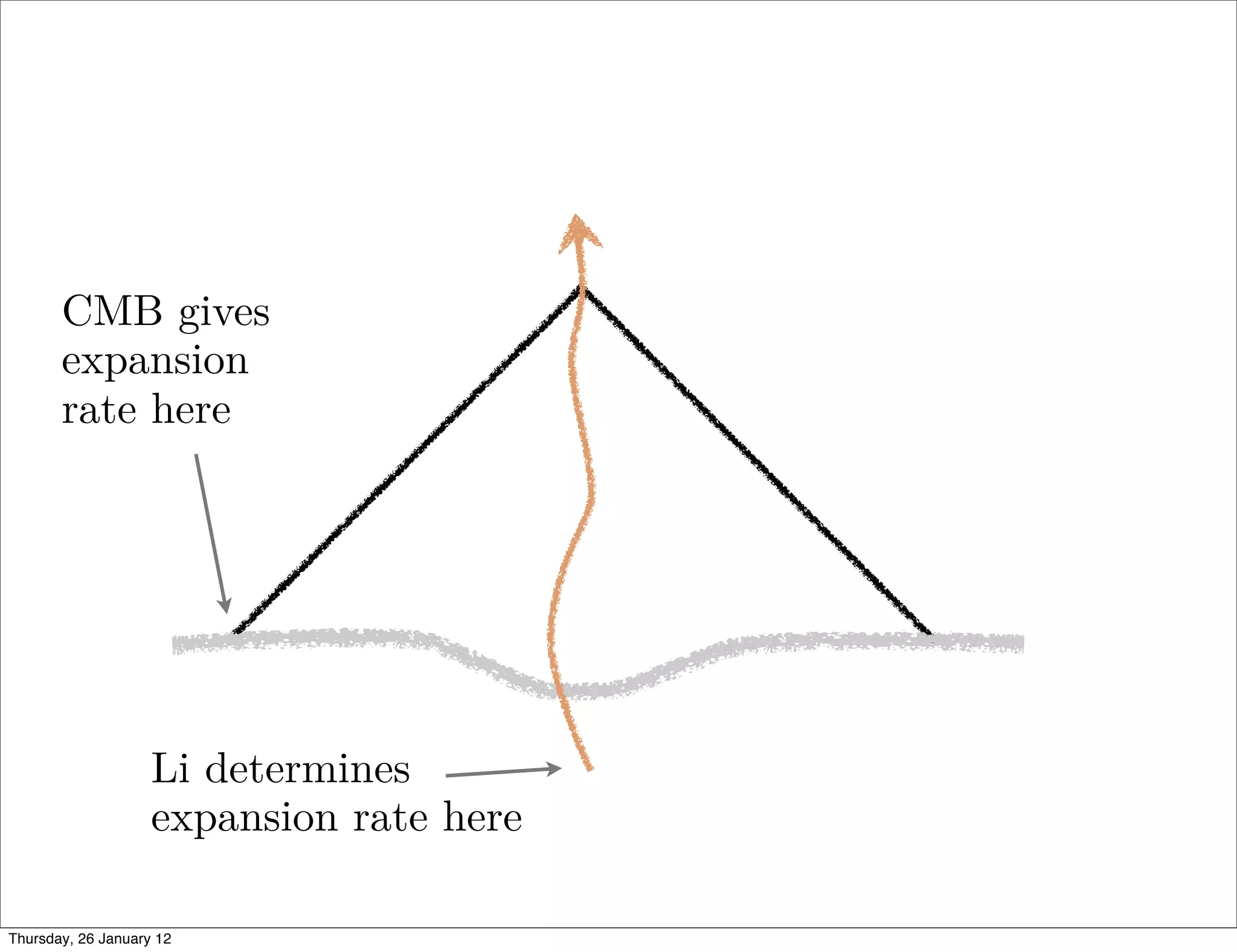
![Lithium problem → inhomogeneity at early times?
• a Gpc fluctuation in baryon-photon ratio solves Li problem
FIG. 1: Constraints on . Top left we estimate current constraints on 10 = 1010 from di erent
7 Do primordial Lithium abundances imply there’s no Dark Energy?
from Li observations [10] in Galactic globular clusters and Galactic halo are shown separately, alon
These agree with each other if 10 ⇠ 4. Local measurements of D are very uncertain [8] though they
Marco Regis and Chris Clarkson
assume the rather precise value we show (from Cosmology analyses inCentre,and an astration factor (i.e.
Astrophysics,
Bayesian & Gravity [11]) and,
Thursday, 26 January 12
formation in our Galaxy) of f ⇠ 2 3. (Or, alternatively, a smaller f [12] with a slightly di erent v](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-43-2048.jpg)
![Lithium problem → inhomogeneity at early times?
• a Gpc fluctuation in baryon-photon ratio solves Li problem
FIG. 1: Constraints on . Top left we estimate current constraints on 10 = 1010 from di erent
7 Do primordial Lithium abundances imply there’s no Dark Energy?
from Li observations [10] in Galactic globular clusters and Galactic halo are shown separately, alon
These agree with each other if 10 ⇠ 4. Local measurements of D are very uncertain [8] though they
Marco Regis and Chris Clarkson
assume the rather precise value we show (from Cosmology analyses inCentre,and an astration factor (i.e.
Astrophysics,
Bayesian & Gravity [11]) and,
Thursday, 26 January 12
formation in our Galaxy) of f ⇠ 2 3. (Or, alternatively, a smaller f [12] with a slightly di erent v](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-44-2048.jpg)
![Lithium problem → inhomogeneity at early times?
• a Gpc fluctuation in baryon-photon ratio solves Li problem
FIG. 1: Constraints on . Top left we estimate current constraints on 10 = 1010 from di erent
7 Do primordial Lithium abundances imply there’s no Dark Energy?
from Li observations [10] in Galactic globular clusters and Galactic halo are shown separately, alon
These agree with each other if 10 ⇠ 4. Local measurements of D are very uncertain [8] though they
Marco Regis and Chris Clarkson
assume the rather precise value we show (from Cosmology analyses inCentre,and an astration factor (i.e.
Astrophysics,
Bayesian & Gravity [11]) and,
Thursday, 26 January 12
formation in our Galaxy) of f ⇠ 2 3. (Or, alternatively, a smaller f [12] with a slightly di erent v](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-45-2048.jpg)
![Lithium problem → inhomogeneity at early times?
• a Gpc fluctuation in baryon-photon ratio solves Li problem
FIG. 1: Constraints on . Top left we estimate current constraints on 10 = 1010 from di erent
7 Do primordial Lithium abundances imply there’s no Dark Energy?
from Li observations [10] in Galactic globular clusters and Galactic halo are shown separately, alon
These agree with each other if 10 ⇠ 4. Local measurements of D are very uncertain [8] though they
Marco Regis and Chris Clarkson
assume the rather precise value we show (from Cosmology analyses inCentre,and an astration factor (i.e.
Astrophysics,
Bayesian & Gravity [11]) and,
Thursday, 26 January 12
formation in our Galaxy) of f ⇠ 2 3. (Or, alternatively, a smaller f [12] with a slightly di erent v](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-46-2048.jpg)
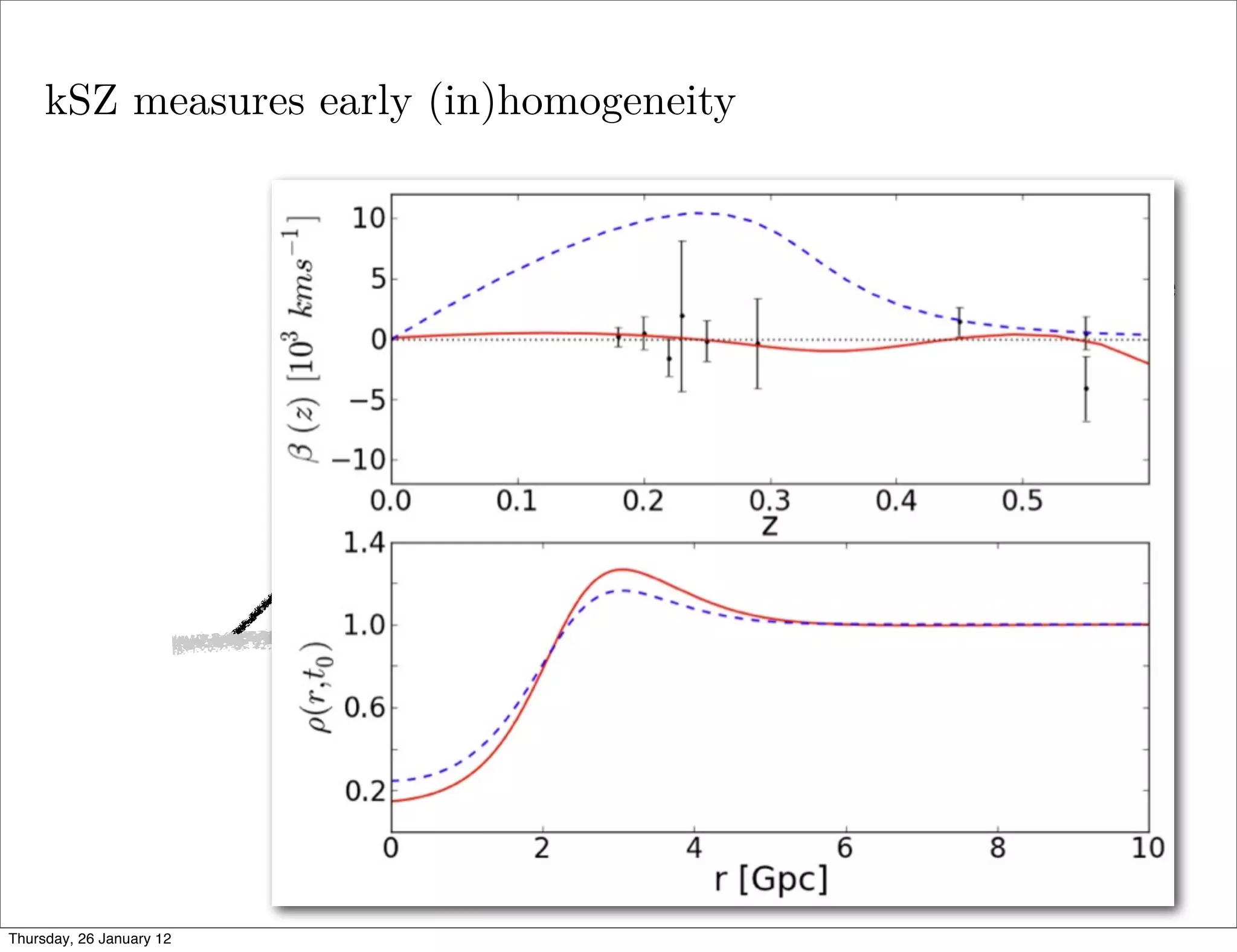
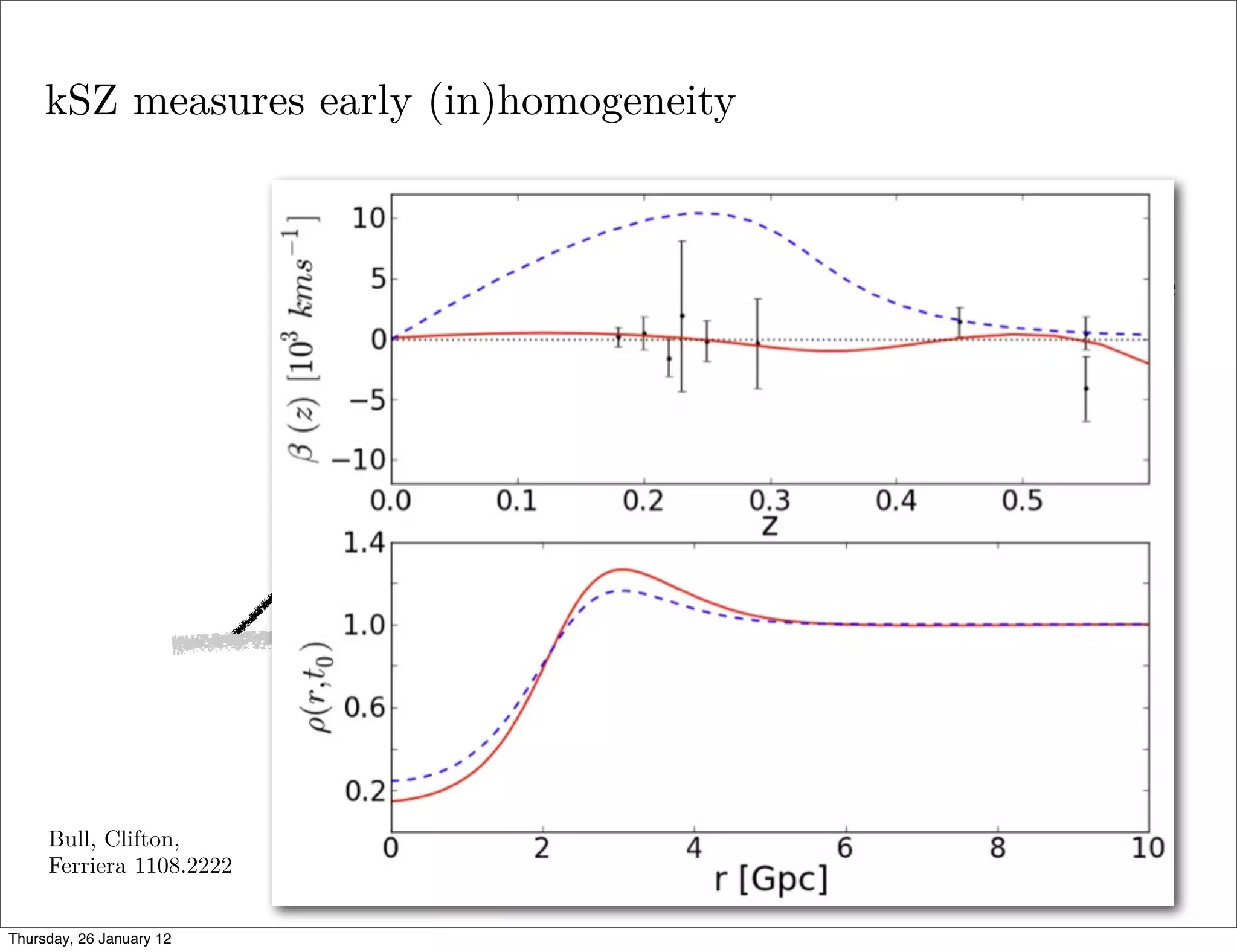
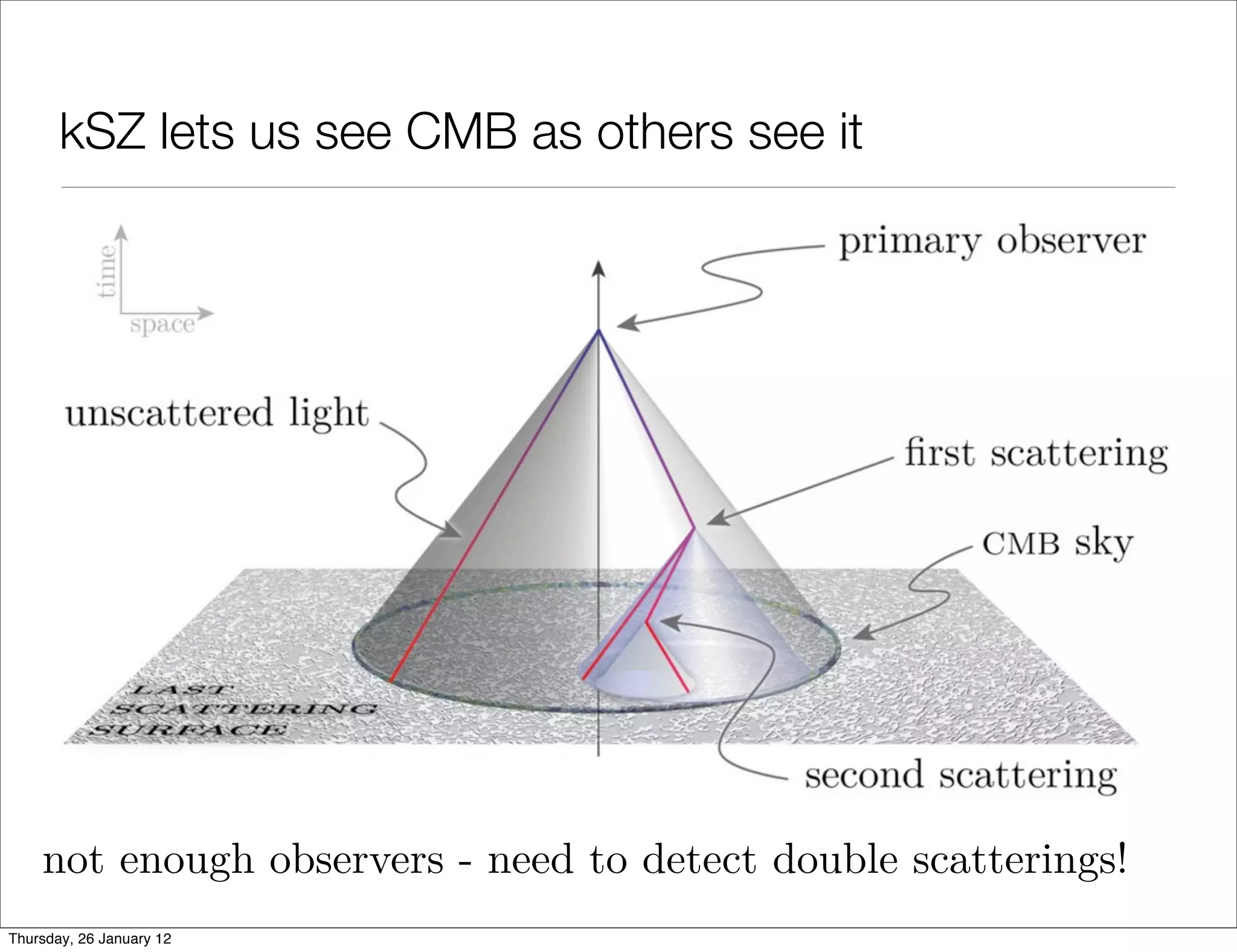
![e 2. Examples of the size of the dipole for different parameters of the constrained
model [19]. strong constraint left figure is the first order approximation
kSZ The dashed line in the
n [30].
• kSZ (and SZ) effect can look inside our past lightcone
!in=0.23, r0=1.8, H0=0.65, "r/r0=0.35
e void in90 eyes - the kSZ effect in LTB models
the 6
8
60
6
30 4
vP [1000 km/s]
2
0 -45 -90 -135
0
-2
-30
Figure 1. An off-centre cluster of galaxies in a void will “observe” CMB photons
-4
coming from the last scattering surface from all directions. Due to the higher expansion
rate inside the void, photons arriving through the centre (from the right in the figure)
will have a larger redshift (∆zin ), than photons arriving directly from the LSS (left,
-60
-6
with ∆zout ). There is a subdominant effect due to the time-dependent density profile
0.0
(the solid line corresponds to the current time, while the dot-dashed line to one tenth of 0.2 0.4 0.6
the present time). With a larger underdensity at later times, we have ∆z1 > ∆z4 , and
-90 Redshift
∆z2 + ∆z3 < 0, giving an overall difference ∆z1 > ∆z2 + ∆z3 + ∆z4 or, equivalently, a
Looking the void in the eyes - the kSZ effect in LTB
subdominant dipole with a blueshift towards the centre of the void. The overall effect
is a blueshift away from the centre.
models
e 3. The angular and redshift distribution of current observations together with
1 1,2
quently, in the ideal case Juan Garc´void, and a well embedded cluster, the
of a sphericalıa-Bellido , Troels Haugbølle
server will see an almost perfect dipole in the CMB, aligned along the radial parsec sized void model. Red triangles and
dicted dipoleInstituto de 28049 Madrid, UAM-CSIC, a gigaAut´noma de Madrid,
1
distribution for Universidad o
F´ısica Te´rica
o
008
Cantoblanco, Spain,
and with the blueshift pointing away from the centre of the void, where the
suares26 January 12 Department of Physics and Astronomy,negative peculiar C,
(see Fig. 1).represent of a spherical void and CMB sky of of Aarhus, DK-8000 Aarhus velocities respectively, with the
The detailed effect positive on the University an
2
Thursday,](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-51-2048.jpg)
![e 2. Examples of the size of the dipole for different parameters of the constrained
model [19]. strong constraint left figure is the first order approximation
kSZ The dashed line in the
n [30].
• kSZ (and SZ) effect can look inside our past lightcone
!in=0.23, r0=1.8, H0=0.65, "r/r0=0.35
e void in90 eyes - the kSZ effect in LTB models
the 6
8
60
6
30 4
vP [1000 km/s]
2
0 -45 -90 -135
0
-2
-30
Figure 1. An off-centre cluster of galaxies in a void will “observe” CMB photons
-4
coming from the last scattering surface from all directions. Due to the higher expansion
rate inside the void, photons arriving through the centre (from the right in the figure)
will have a larger redshift (∆zin ), than photons arriving directly from the LSS (left,
-60
-6
with ∆zout ). There is a subdominant effect due to the time-dependent density profile
0.0
(the solid line corresponds to the current time, while the dot-dashed line to one tenth of 0.2 0.4 0.6
the present time). With a larger underdensity at later times, we have ∆z1 > ∆z4 , and
-90 Redshift
∆z2 + ∆z3 < 0, giving an overall difference ∆z1 > ∆z2 + ∆z3 + ∆z4 or, equivalently, a
Looking the void in the eyes - the kSZ effect in LTB
subdominant dipole with a blueshift towards the centre of the void. The overall effect
is a blueshift away from the centre.
models
e 3. The angular and redshift distribution of current observations together with
1 1,2
quently, in the ideal case Juan Garc´void, and a well embedded cluster, the
of a sphericalıa-Bellido , Troels Haugbølle
server will see an almost perfect dipole in the CMB, aligned along the radial parsec sized void model. Red triangles and
dicted dipoleInstituto de 28049 Madrid, UAM-CSIC, a gigaAut´noma de Madrid,
1
distribution for Universidad o
F´ısica Te´rica
o
008
Cantoblanco, Spain,
and with the blueshift pointing away from the centre of the void, where the
suares26 January 12 Department of Physics and Astronomy,negative peculiar C,
(see Fig. 1).represent of a spherical void and CMB sky of of Aarhus, DK-8000 Aarhus velocities respectively, with the
The detailed effect positive on the University an
2
Thursday,](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-52-2048.jpg)
![e 2. Examples of the size of the dipole for different parameters of the constrained
model [19]. strong constraint left figure is the first order approximation
kSZ The dashed line in the
n [30].
• kSZ (and SZ) effect can look inside our past lightcone
!in=0.23, r0=1.8, H0=0.65, "r/r0=0.35
e void in90 eyes - the kSZ effect in LTB models
the 6
8
60
6
30 4
vP [1000 km/s]
2
0 -45 -90 -135
0
-2
-30
Figure 1. An off-centre cluster of galaxies in a void will “observe” CMB photons
-4
coming from the last scattering surface from all directions. Due to the higher expansion
rate inside the void, photons arriving through the centre (from the right in the figure)
will have a larger redshift (∆zin ), than photons arriving directly from the LSS (left,
-60
-6
with ∆zout ). There is a subdominant effect due to the time-dependent density profile
0.0
(the solid line corresponds to the current time, while the dot-dashed line to one tenth of 0.2 0.4 0.6
the present time). With a larger underdensity at later times, we have ∆z1 > ∆z4 , and
-90 Redshift
∆z2 + ∆z3 < 0, giving an overall difference ∆z1 > ∆z2 + ∆z3 + ∆z4 or, equivalently, a
Looking the void in the eyes - the kSZ effect in LTB
subdominant dipole with a blueshift towards the centre of the void. The overall effect
is a blueshift away from the centre.
models
e 3. The angular and redshift distribution of current observations together with
1 1,2
quently, in the ideal case Juan Garc´void, and a well embedded cluster, the
of a sphericalıa-Bellido , Troels Haugbølle
server will see an almost perfect dipole in the CMB, aligned along the radial parsec sized void model. Red triangles and
dicted dipoleInstituto de 28049 Madrid, UAM-CSIC, a gigaAut´noma de Madrid,
1
distribution for Universidad o
F´ısica Te´rica
o
008
Cantoblanco, Spain,
and with the blueshift pointing away from the centre of the void, where the
suares26 January 12 Department of Physics and Astronomy,negative peculiar C,
(see Fig. 1).represent of a spherical void and CMB sky of of Aarhus, DK-8000 Aarhus velocities respectively, with the
The detailed effect positive on the University an
2
Thursday,](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-53-2048.jpg)
![e 2. Examples of the size of the dipole for different parameters of the constrained
model [19]. strong constraint left figure is the first order approximation
kSZ The dashed line in the
n [30].
• kSZ (and SZ) effect can look inside our past lightcone
!in=0.23, r0=1.8, H0=0.65, "r/r0=0.35
e void in90 eyes - the kSZ effect in LTB models
the 6
8
60
6
30 4
vP [1000 km/s]
2
0 -45 -90 -135
0
-2
-30
Figure 1. An off-centre cluster of galaxies in a void will “observe” CMB photons
-4
coming from the last scattering surface from all directions. Due to the higher expansion
rate inside the void, photons arriving through the centre (from the right in the figure)
will have a larger redshift (∆zin ), than photons arriving directly from the LSS (left,
-60
-6
with ∆zout ). There is a subdominant effect due to the time-dependent density profile
0.0
(the solid line corresponds to the current time, while the dot-dashed line to one tenth of 0.2 0.4 0.6
the present time). With a larger underdensity at later times, we have ∆z1 > ∆z4 , and
-90 Redshift
∆z2 + ∆z3 < 0, giving an overall difference ∆z1 > ∆z2 + ∆z3 + ∆z4 or, equivalently, a
Looking the void in the eyes - the kSZ effect in LTB
subdominant dipole with a blueshift towards the centre of the void. The overall effect
is a blueshift away from the centre.
models
e 3. The angular and redshift distribution of current observations together with
1 1,2
quently, in the ideal case Juan Garc´void, and a well embedded cluster, the
of a sphericalıa-Bellido , Troels Haugbølle
server will see an almost perfect dipole in the CMB, aligned along the radial parsec sized void model. Red triangles and
dicted dipoleInstituto de 28049 Madrid, UAM-CSIC, a gigaAut´noma de Madrid,
1
distribution for Universidad o
F´ısica Te´rica
o
008
Cantoblanco, Spain,
and with the blueshift pointing away from the centre of the void, where the
suares26 January 12 Department of Physics and Astronomy,negative peculiar C,
(see Fig. 1).represent of a spherical void and CMB sky of of Aarhus, DK-8000 Aarhus velocities respectively, with the
The detailed effect positive on the University an
2
Thursday,](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-54-2048.jpg)
![e 2. Examples of the size of the dipole for different parameters of the constrained
model [19]. strong constraint left figure is the first order approximation
kSZ The dashed line in the
n [30].
• kSZ (and SZ) effect can look inside our past lightcone
!in=0.23, r0=1.8, H0=0.65, "r/r0=0.35
e void in90 eyes - the kSZ effect in LTB models
the 6
8
60
6
30 4
vP [1000 km/s]
2
0 -45 -90 -135
0
-2
-30
Figure 1. An off-centre cluster of galaxies in a void will “observe” CMB photons
-4
coming from the last scattering surface from all directions. Due to the higher expansion
rate inside the void, photons arriving through the centre (from the right in the figure)
will have a larger redshift (∆zin ), than photons arriving directly from the LSS (left,
-60
-6
with ∆zout ). There is a subdominant effect due to the time-dependent density profile
0.0
(the solid line corresponds to the current time, while the dot-dashed line to one tenth of 0.2 0.4 0.6
the present time). With a larger underdensity at later times, we have ∆z1 > ∆z4 , and
-90 Redshift
∆z2 + ∆z3 < 0, giving an overall difference ∆z1 > ∆z2 + ∆z3 + ∆z4 or, equivalently, a
Looking the void in the eyes - the kSZ effect in LTB
subdominant dipole with a blueshift towards the centre of the void. The overall effect
is a blueshift away from the centre.
models
e 3. The angular and redshift distribution of current observations together with
1 1,2
quently, in the ideal case Juan Garc´void, and a well embedded cluster, the
of a sphericalıa-Bellido , Troels Haugbølle
server will see an almost perfect dipole in the CMB, aligned along the radial parsec sized void model. Red triangles and
dicted dipoleInstituto de 28049 Madrid, UAM-CSIC, a gigaAut´noma de Madrid,
1
distribution for Universidad o
F´ısica Te´rica
o
008
Cantoblanco, Spain,
and with the blueshift pointing away from the centre of the void, where the
suares26 January 12 Department of Physics and Astronomy,negative peculiar C,
(see Fig. 1).represent of a spherical void and CMB sky of of Aarhus, DK-8000 Aarhus velocities respectively, with the
The detailed effect positive on the University an
2
Thursday,](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-55-2048.jpg)
![so...
• voids fit key background observations [just!]: SN+H0+CMB
• but simplest ‘adiabatic’ voids ruled out - probably not solution to DE!
• they assume everything homogeneous except matter density
• does that make sense?
• if we don’t have a theory to make a void, we can only make a map of it
• everything could be inhomogeneous ... what measures what?
Thursday, 26 January 12](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-57-2048.jpg)




![when does CP imply homogeneity ?
• if everyone sees an isotropic CMB => homo [Ehlers, Geren, Sachs, 1968]
• if everyone sees isotropic distances => homo [Hasse, Perlick, 199..]
• etc
• can we see the universe from anywhere else?
• do we need to?
Thursday, 26 January 12](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-67-2048.jpg)
![‘on lightcone’ test
• in FLRW we can combine Hubble rate and distance data to find curvature
2
[H(z)D (z)] 1
k =
[H0 D(z)]2
⇥
dL = (1 + z)D = (1 + z) dA
2
• independent of all other cosmological parameters, including dark energy
model, and theory of gravity
• tests the Copernican principle and the basis of FLRW
⇥
C (z) = 1 + H 2
DD D 2
+ HH DD = 0
Clarkson, Basset & Lu, PRL 100 191303
Thursday, 26 January 12](https://image.slidesharecdn.com/testingthecopernicanprincipleintheshadowofdarkenergy-ctsic2012-120201091154-phpapp01/75/Chris-Clarkson-Testing-the-Copernican-Principle-70-2048.jpg)