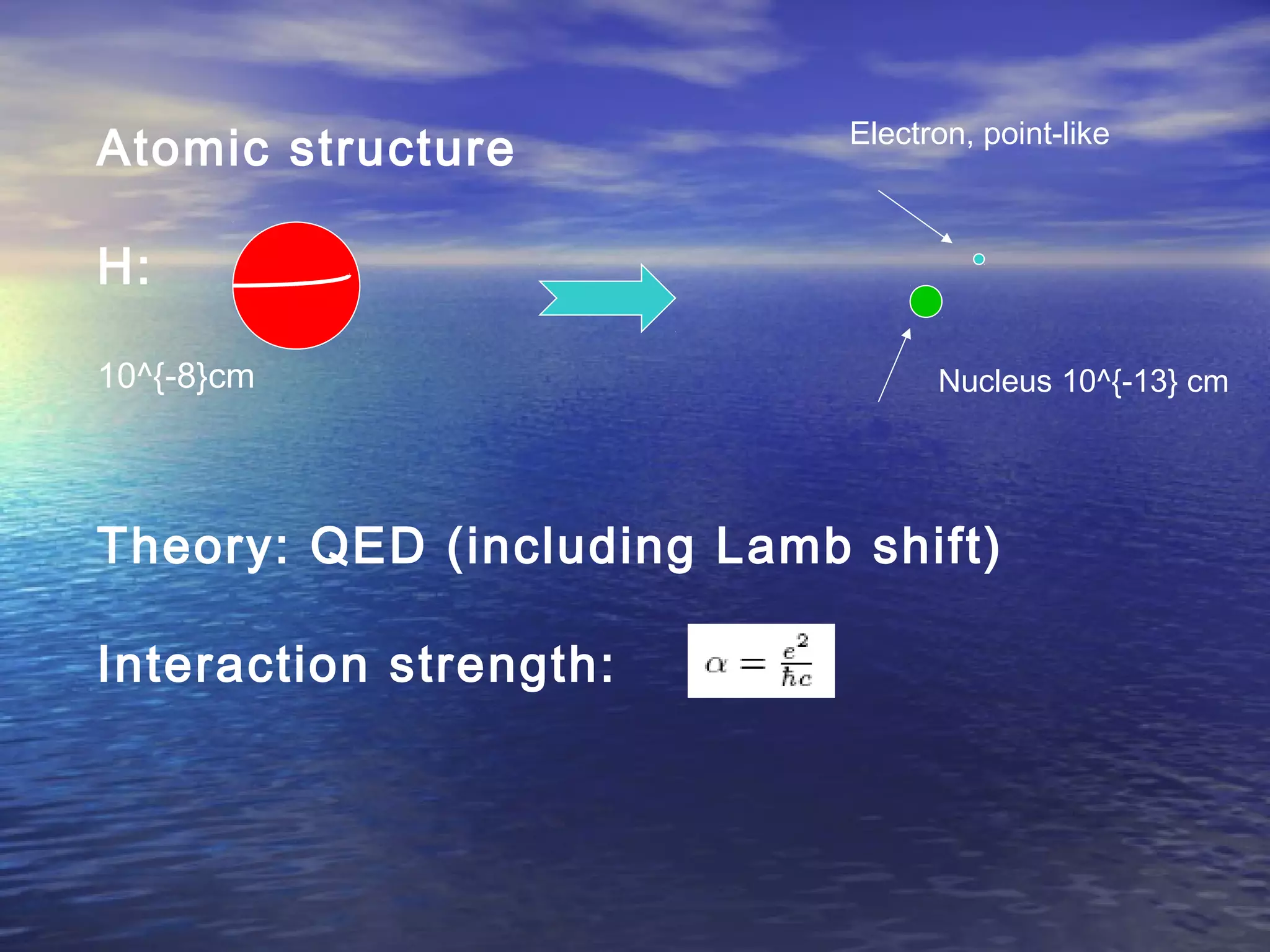
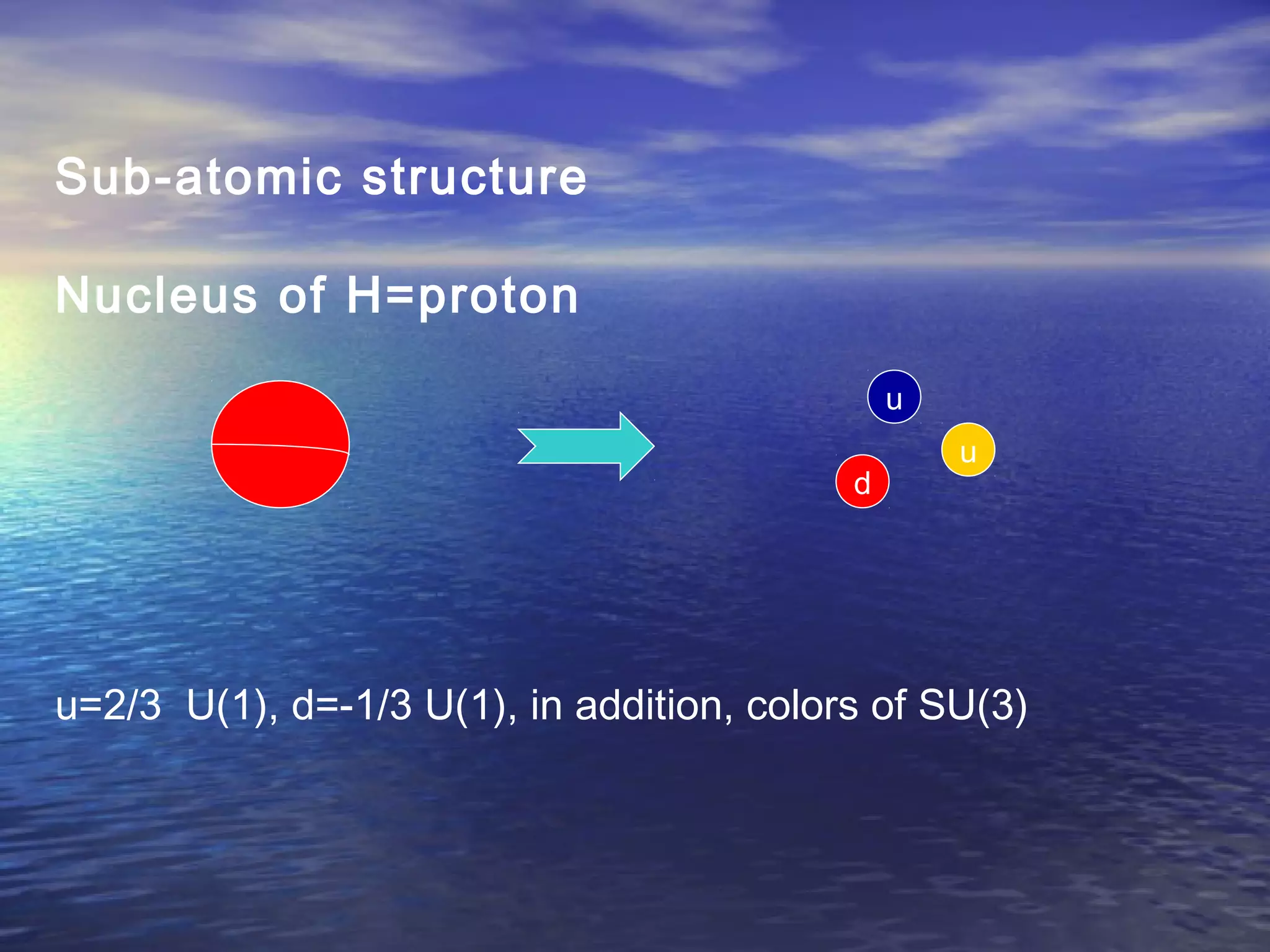
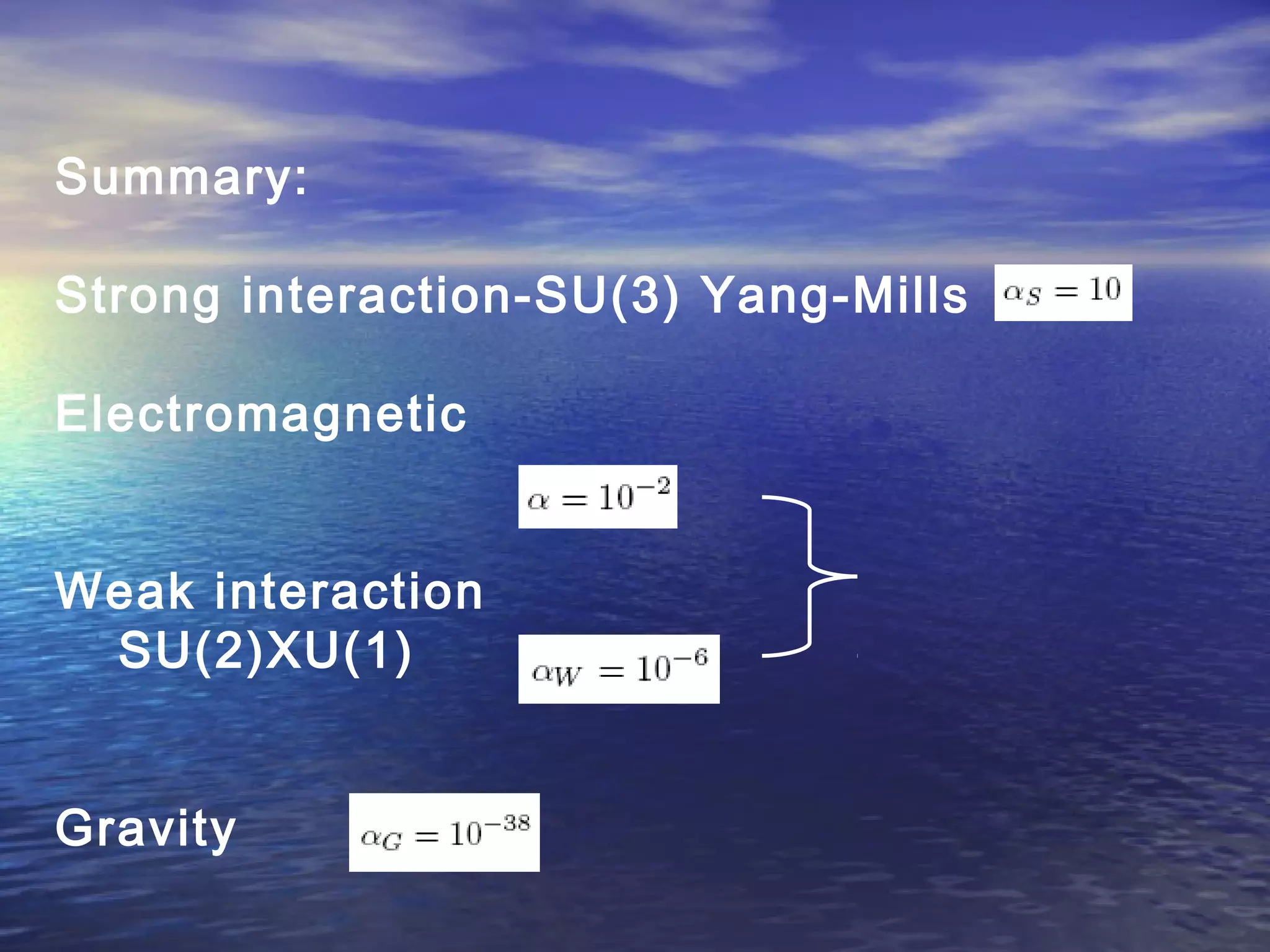
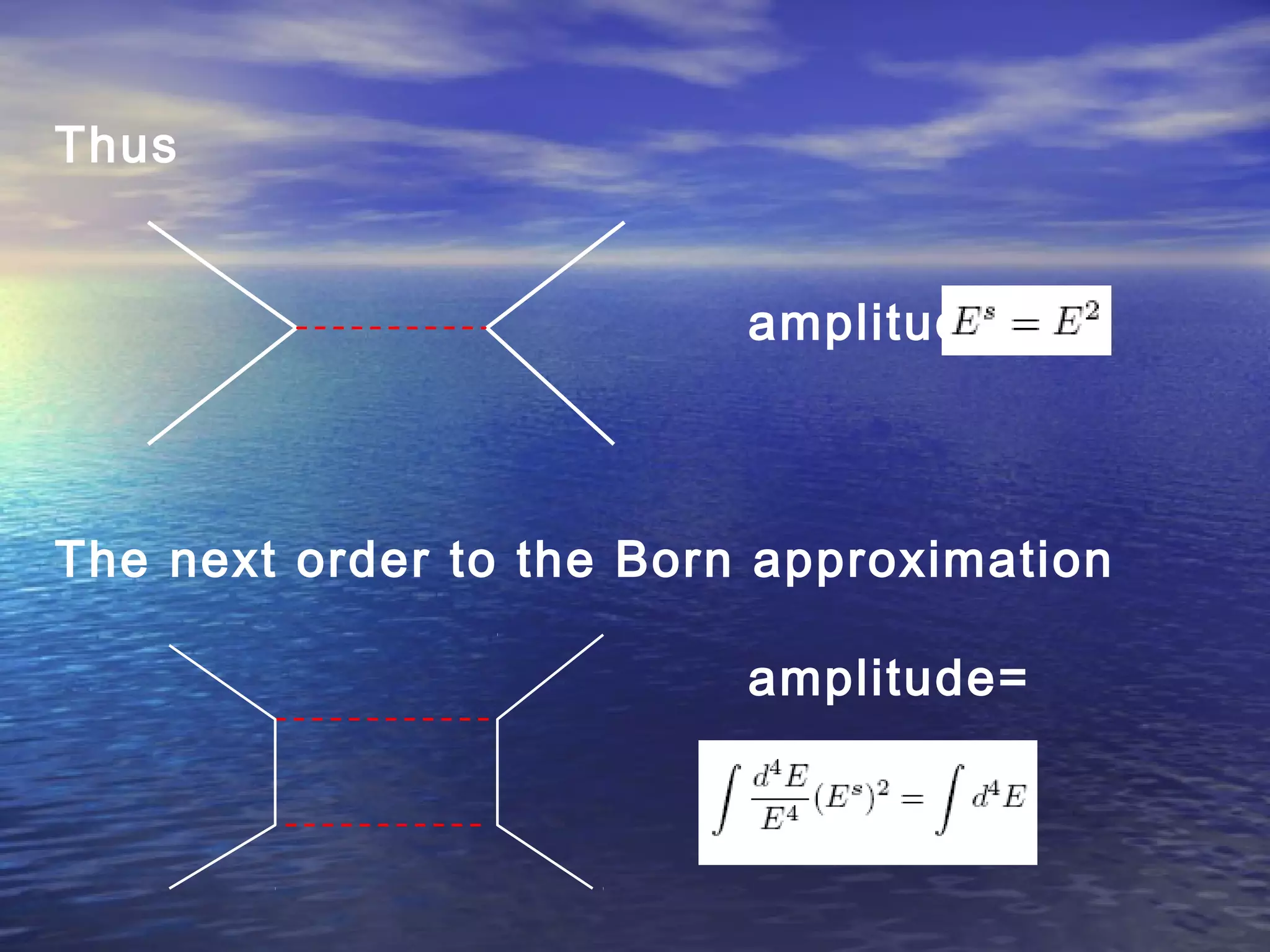
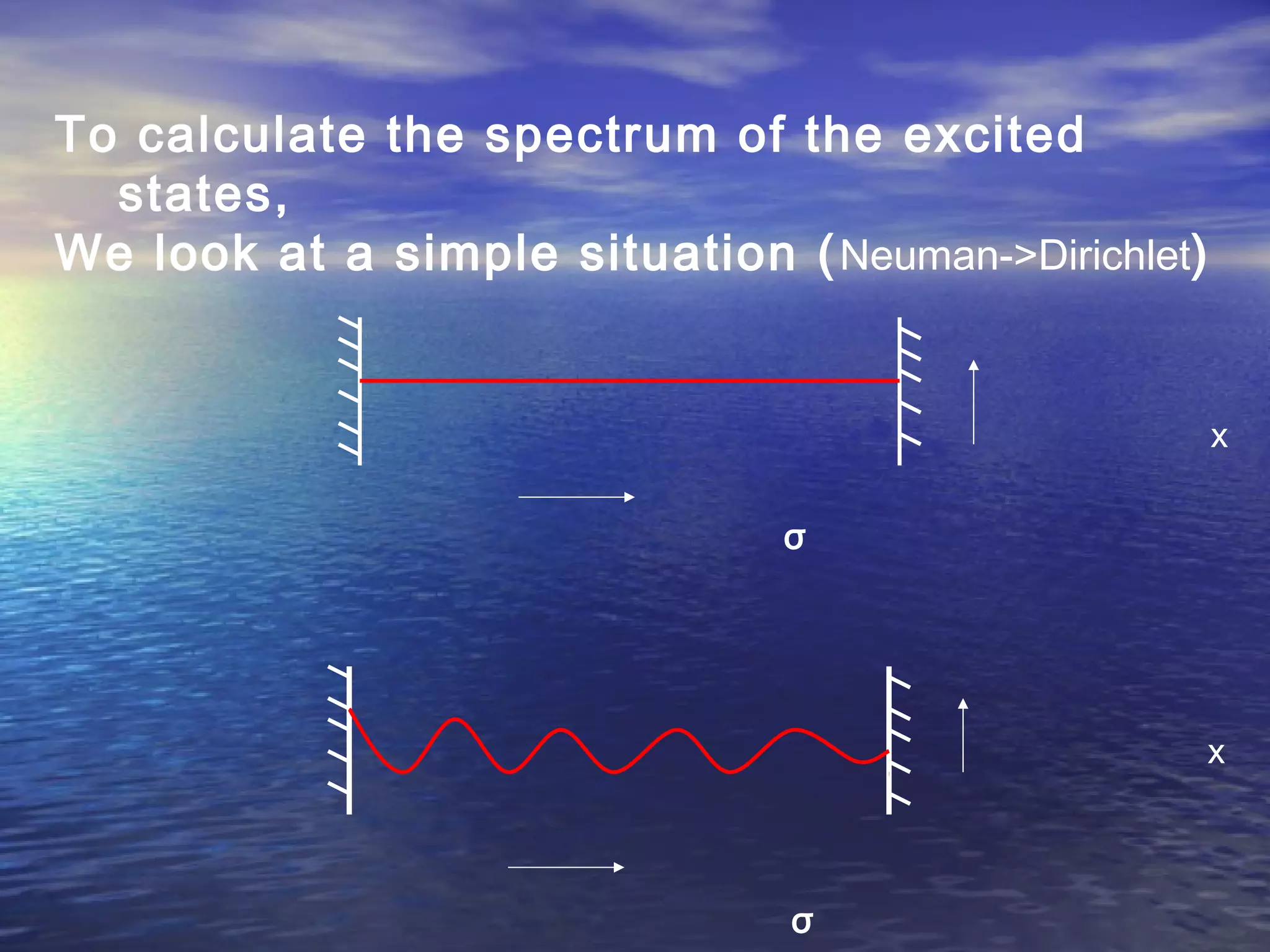
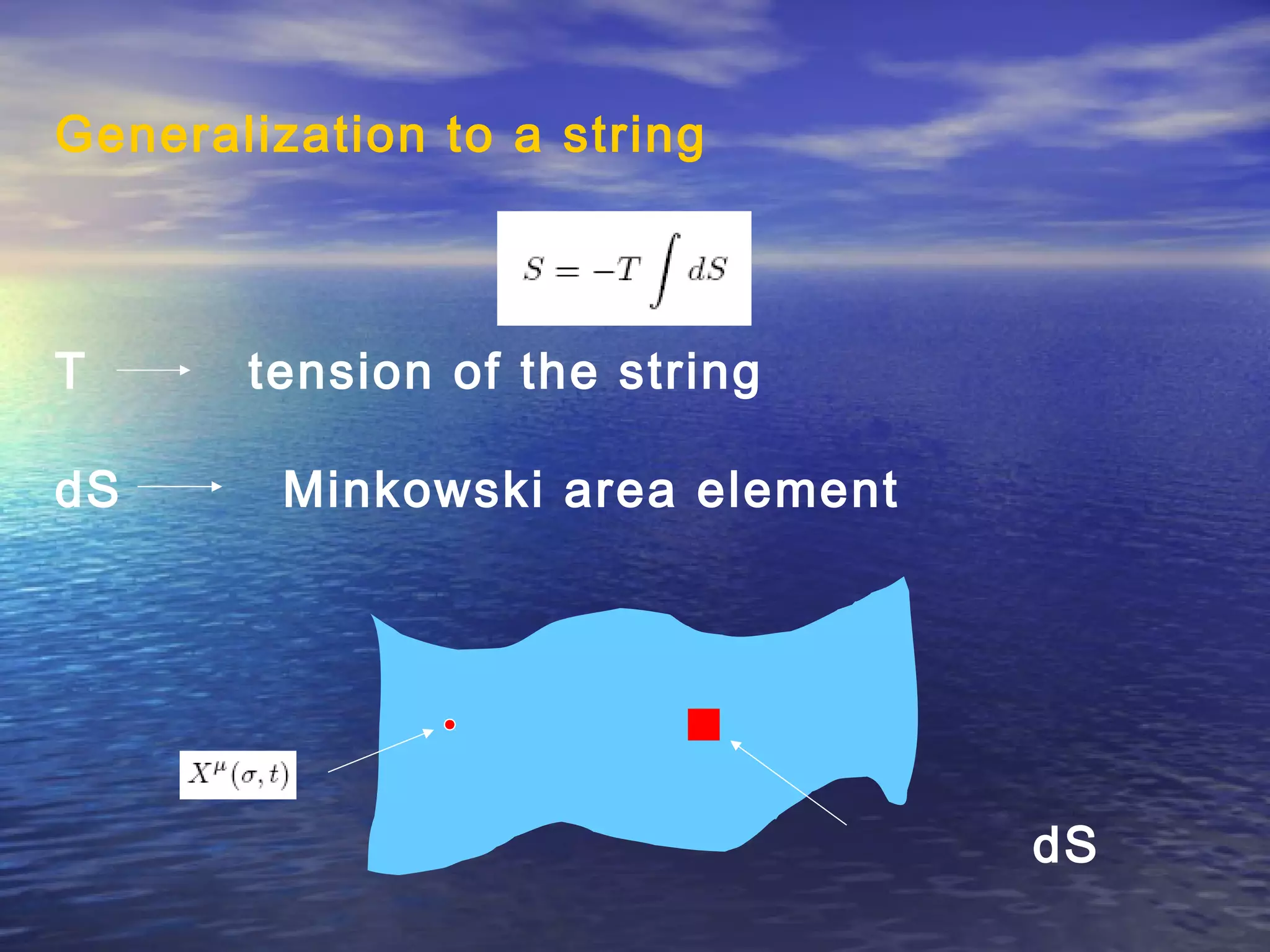
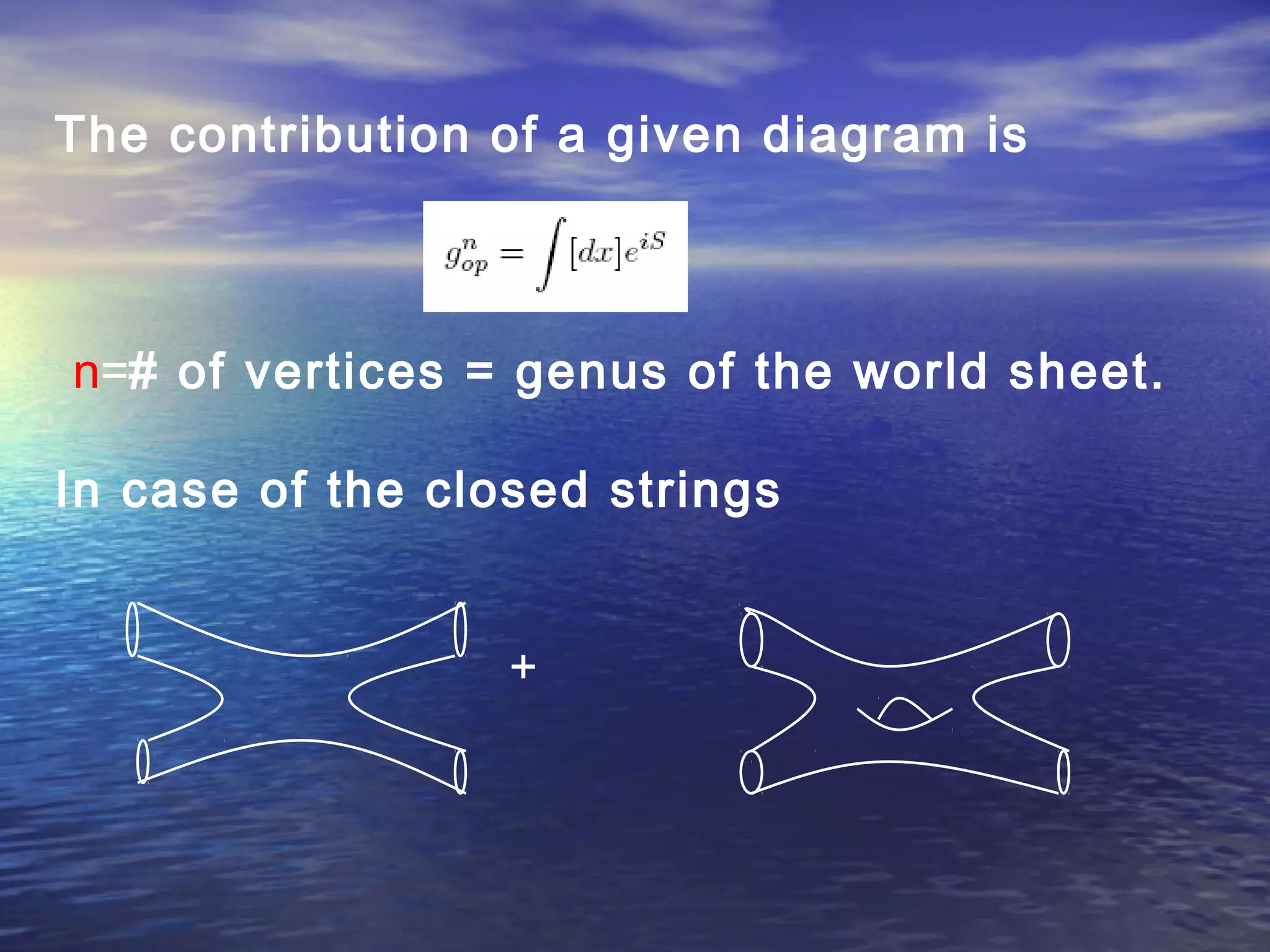
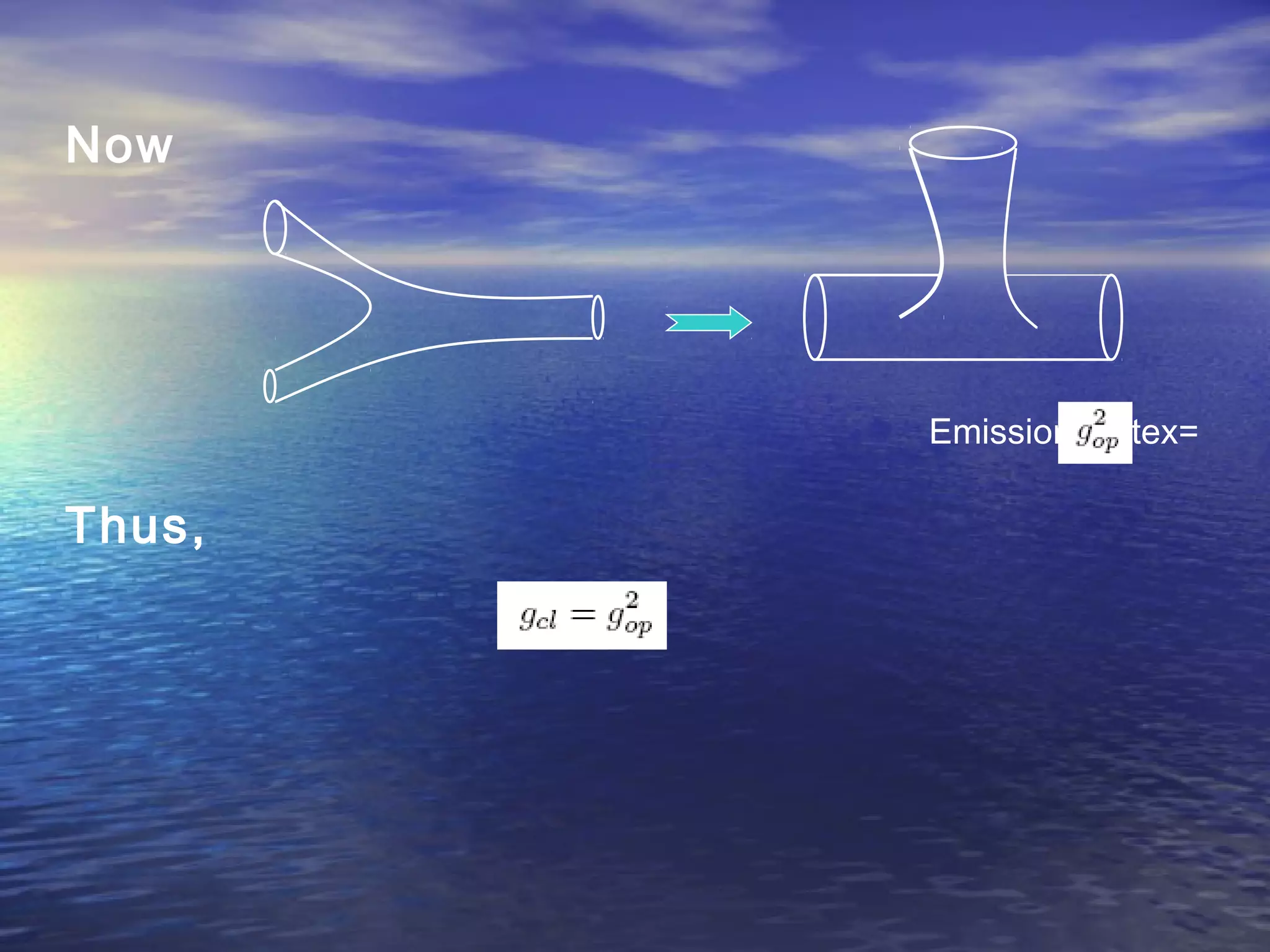
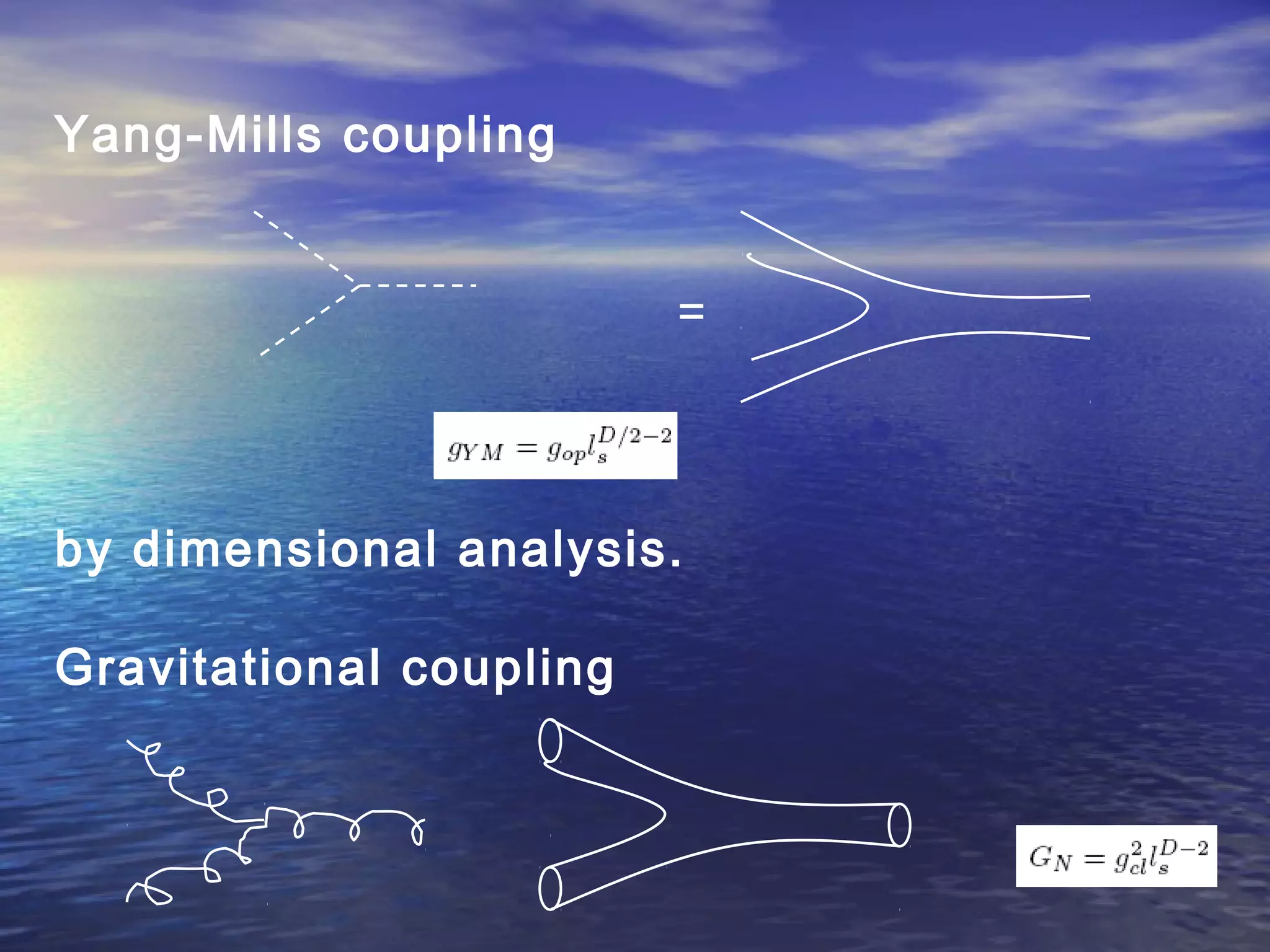
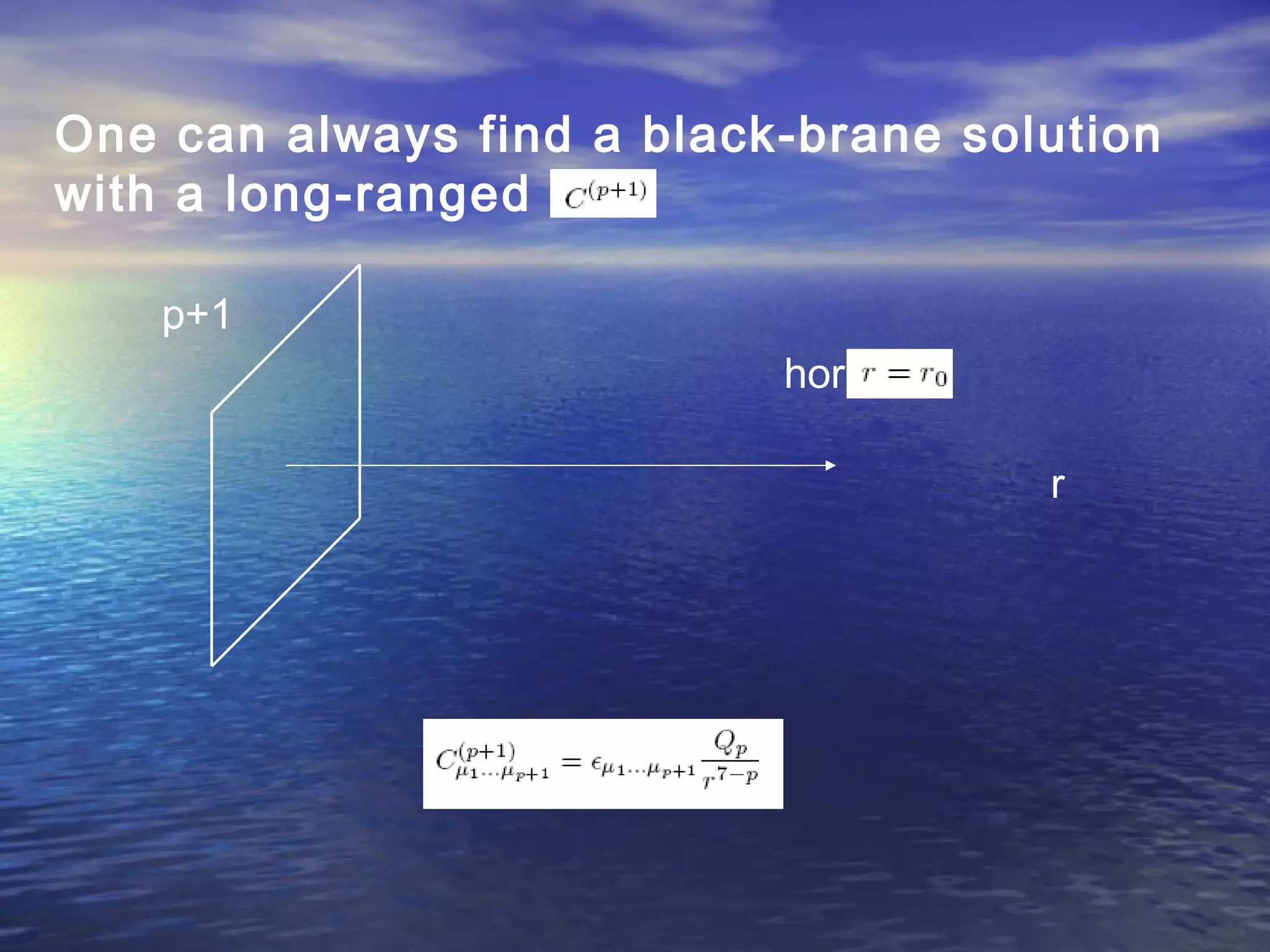
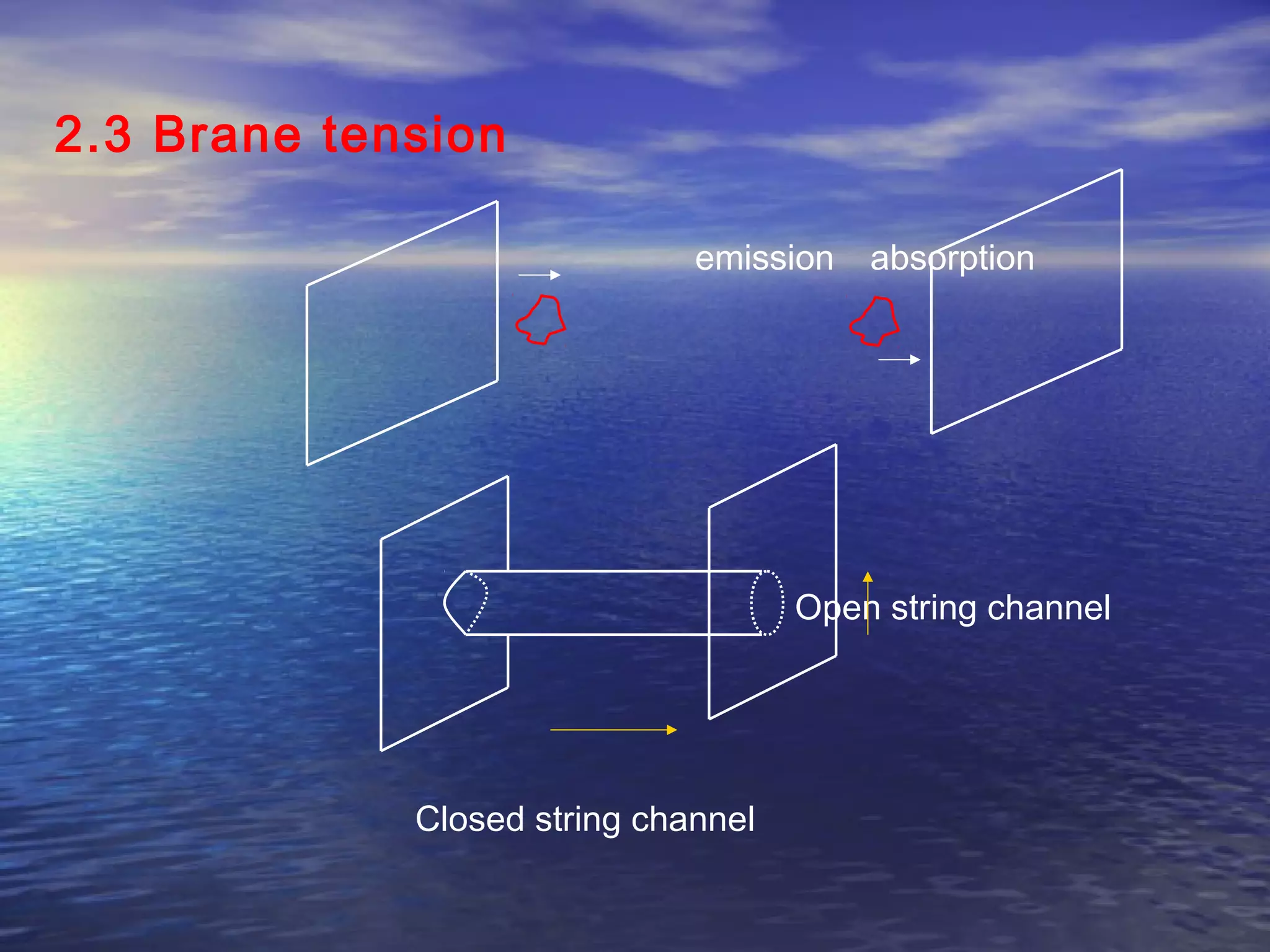
This document provides an outline of string theory. It begins with background on reductionism in physics and the unification of forces. String theory emerged as a way to address difficulties in quantizing gravity. There are five consistent string theories in 10 dimensions: type I open superstring theory with oriented strings; type IIA closed superstring theory with two independent sets of supersymmetry; heterotic string theories that combine bosonic and supersymmetric strings. String theory led to the discovery of supersymmetry and relates fundamental forces and particles to vibrational modes of strings.