Francesca Giordano's presentation discusses the challenges of describing the fundamental state of quantum chromodynamics (QCD) as of 2013, focusing on the concepts of transversity and helicity distributions within protons. Key points include the differences between helicity and transversity distributions, which arise due to the motion of quarks, and the need for complementary reactions to access transversity in experiments. The document also addresses how parton distribution functions, such as helicity and transversity distributions, can be measured through polarized deep inelastic scattering processes.

1. Francesca Giordano
QCD Frontier 2013
JLab, Newport News, VA
Chasing
Transversity
1

2. Francesca Giordano
Proton Structure
2
1970s:
Quantum ChromoDynamics
2013:
still not able to describe QCD
fundamental state

3. Francesca Giordano 3
GPDs (x, bT)
TMDs (x, kT)
x
zy
kT
S
xp
xz
y
xp
bT
PDFs (x)
∫ TMDs(x,kT) ... dkT∫ GPDs(x,bT) ... dbT
Form Factors (t)
Fourier transform (bT)
& ∫ GPDs(x, t) ... dx
Proton Structure

4. Francesca Giordano 4
G
+
momentum frame, these number densities are related to the helicity distrib
the difference of the probability to find a quark polarised along or against t
eigenstate:
gq
1 (x) = q
!)
(x) q
!(
(x).
The momentum distribution measuring the spin average is given by the sum
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin eigen
transversity distribution hq
1 (x) measures the difference of the number dens
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is illust
Differences between the helicity and transversity distributions are a conseq
motion of the quarks within the nucleon. Euclidean rotations and Lorentz
and thus longitudinally polarised nucleons cannot be converted in transverse
infinite momentum. Only in case of non-relativistic quarks both distributions
Another difference emerges from an analysis of helicity amplitudes. F
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0) =
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleon
0 0
q
Momentum distribution

5. Francesca Giordano
the virtual photon selects only quarks of one polarisation, measurements
anti-parallel (!() or parallel polarisations (!)) of lepton (!) and target nu
to number densities q of quarks polarised along or against the nucleon po
momentum frame, these number densities are related to the helicity distri
the difference of the probability to find a quark polarised along or against
eigenstate:
gq
1 (x) = q
!)
(x) q
!(
(x).
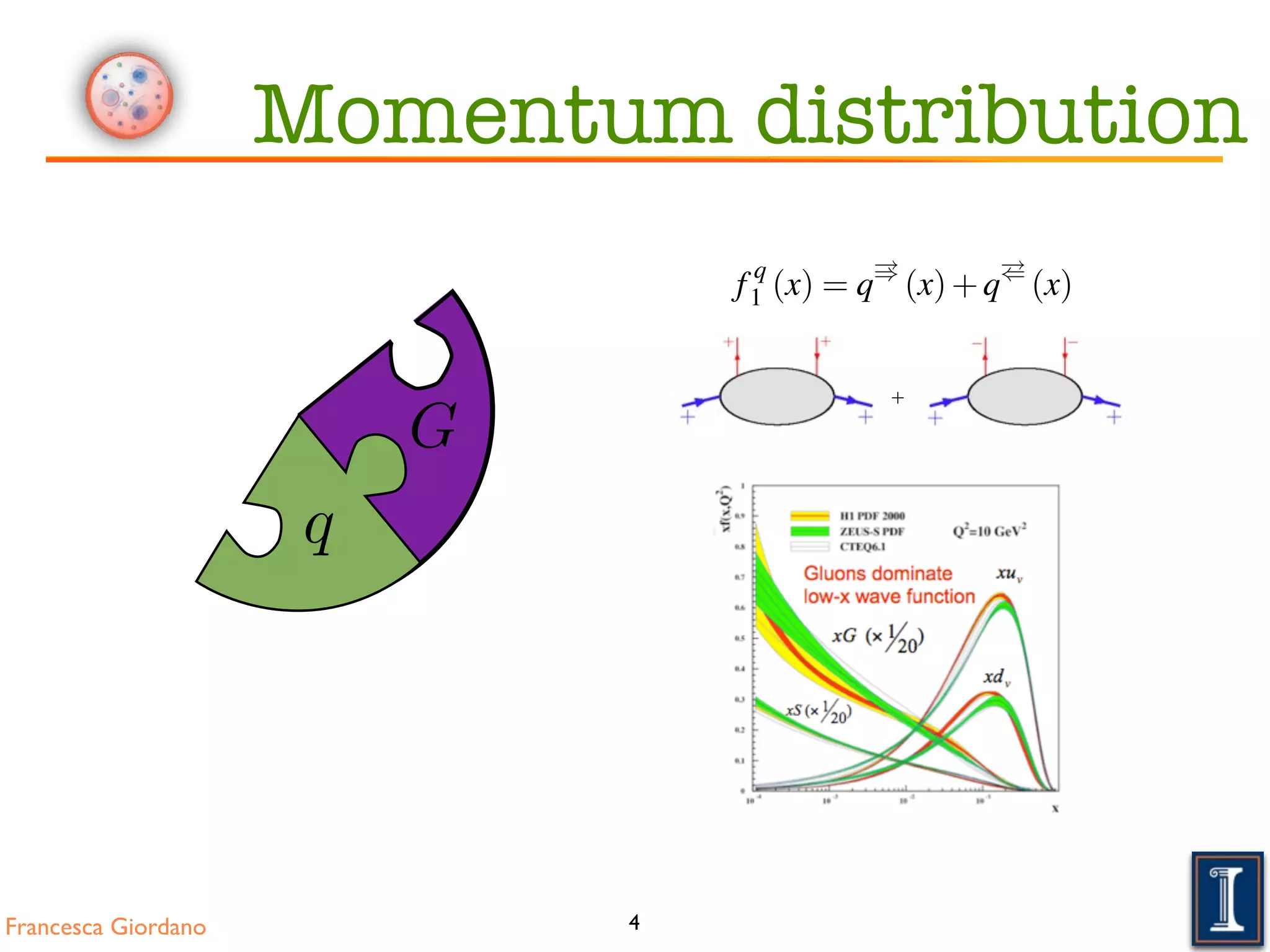
The momentum distribution measuring the spin average is given by the sum
f q
1 (x) = q
!)
(x)+q
!(
(x).
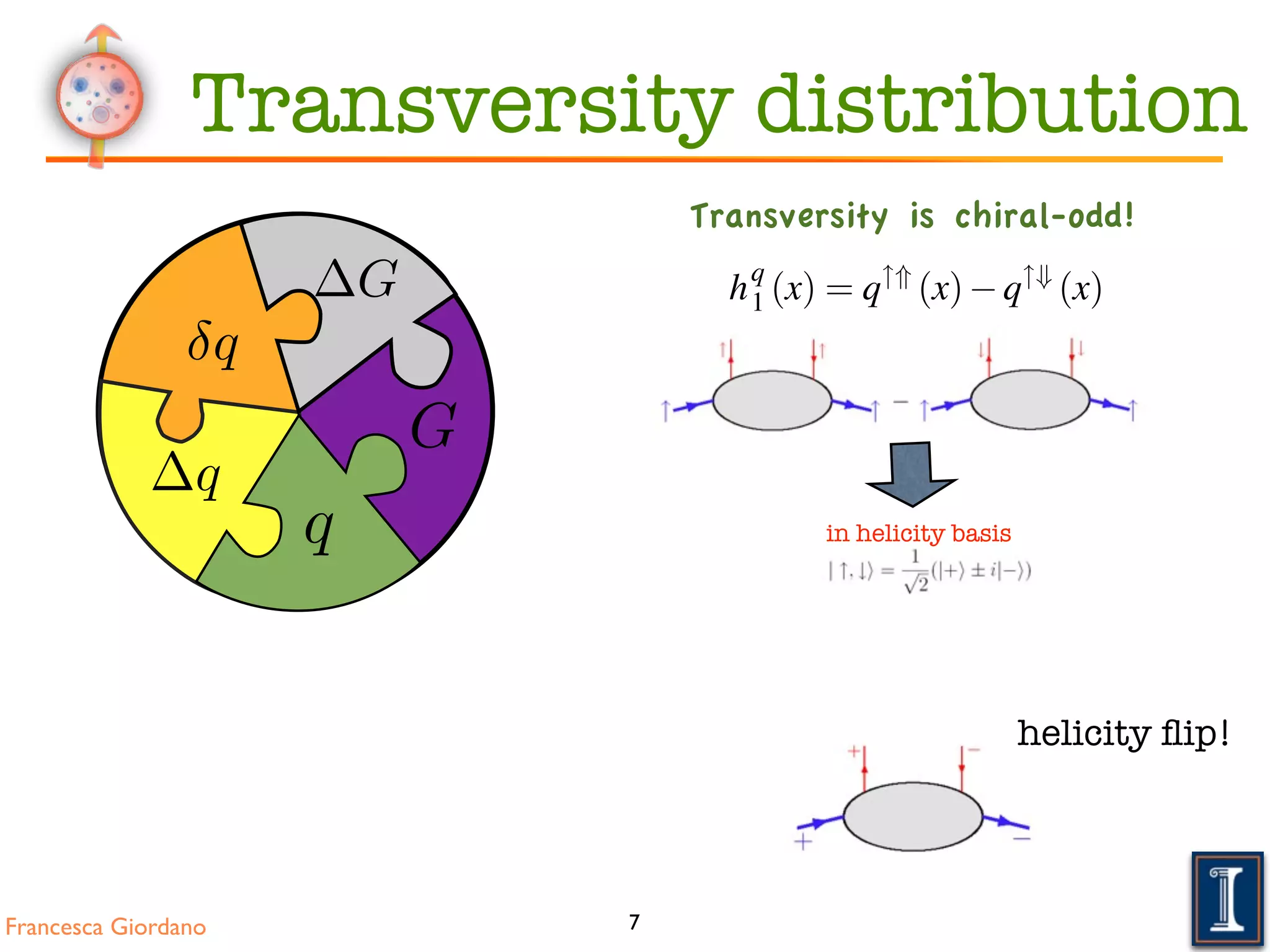
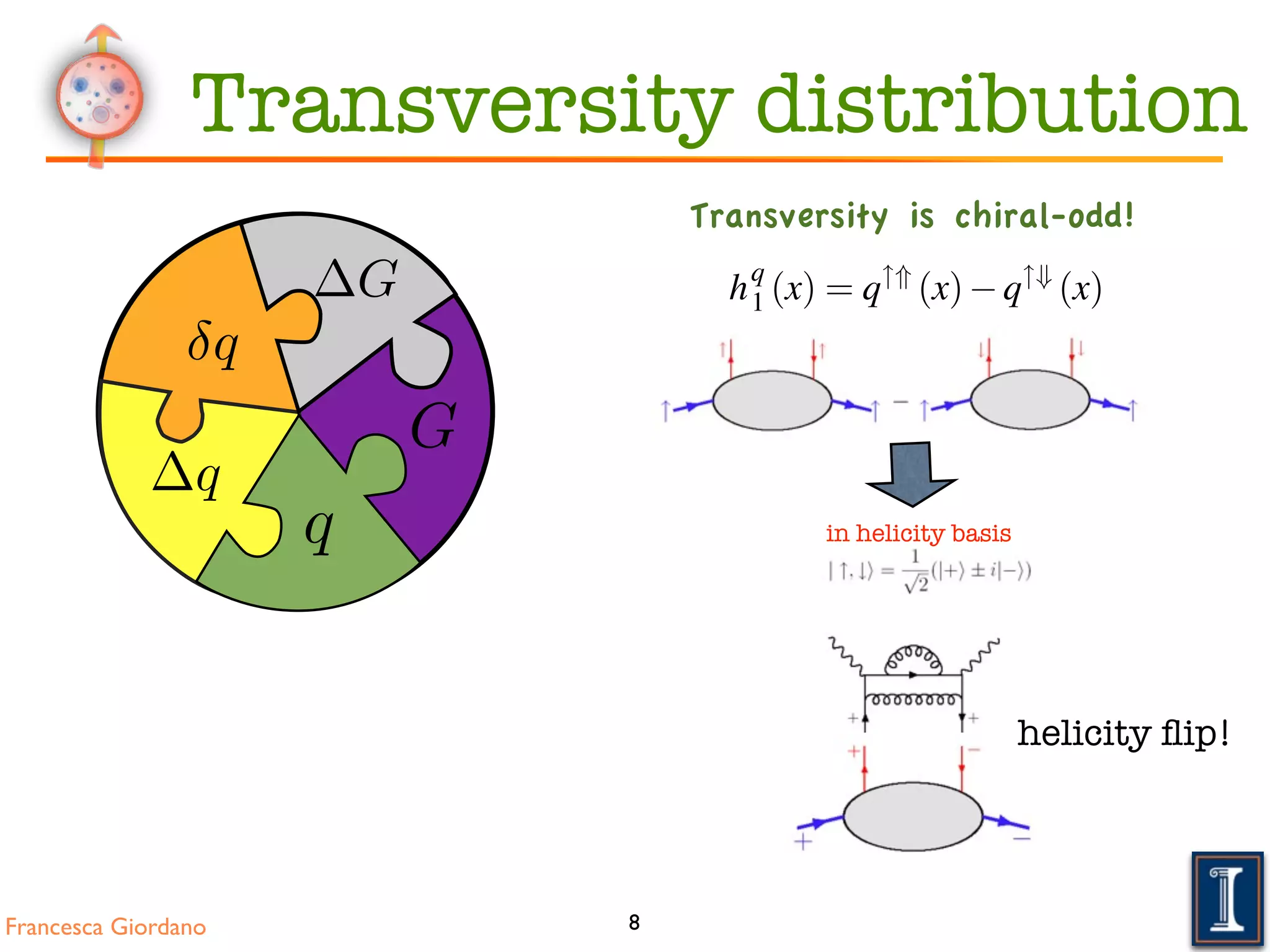
Transversely polarised nucleons In the basis of transverse spin eig
transversity distribution hq
1 (x) measures the difference of the number den
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is illu
Differences between the helicity and transversity distributions are a conse
motion of the quarks within the nucleon. Euclidean rotations and Lorentz
and thus longitudinally polarised nucleons cannot be converted in transvers
infinite momentum. Only in case of non-relativistic quarks both distributio5
TABLE IV: Truncated first moments, ∆f
1,[0.001→1]
i , and full ones, ∆
x-range in Eq. (35) Q2
[GeV2
] ∆u + ∆¯u ∆d + ∆ ¯d ∆¯u
0.001-1.0 1 0.809 -0.417 0.03
4 0.798 -0.417 0.03
10 0.793 -0.416 0.02
100 0.785 -0.412 0.02
0.0-1.0 1 0.817 -0.453 0.03
4 0.814 -0.456 0.03
10 0.813 -0.458 0.03
100 0.812 -0.459 0.03
0
0.1
0.2
0.3
0.4
-0.15
-0.1
-0.05
0
0.05
-0.04
-0.02
0
0.02
-0.04
-0.02
0
0.02
0.02
x(Δu + Δu
–
) x(Δd + Δd
–
)
DSSV
xΔu
–
xΔd
–
xΔs
–
xΔg 0.1
-0.004
-0.002
0
0.002
0.004
FIG. 4: Un
global fit, c
the Hessian
ing PHENI
G
G
q
G
q
Helicity distribution

6. Francesca Giordano
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin ei
transversity distribution hq
1 (x) measures the difference of the number de
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is ill
Differences between the helicity and transversity distributions are a con
motion of the quarks within the nucleon. Euclidean rotations and Loren
and thus longitudinally polarised nucleons cannot be converted in transve
infinite momentum. Only in case of non-relativistic quarks both distributi
Another difference emerges from an analysis of helicity amplitudes
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0)
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleo
emission of the quark (l0) by the nucleon (Λ0). Due to conservation of
parity, AΛlΛ0l0 = A Λ l Λ0 l0 and time reversal there are exactly three i
A++,++, A+ ,+ A+ , +.
The optical theorem relates the forward quark-nucleon scattering amplitu6
G
q
q
q
G
Transversity distribution

7. Francesca Giordano
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin ei
transversity distribution hq
1 (x) measures the difference of the number de
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is ill
Differences between the helicity and transversity distributions are a con
motion of the quarks within the nucleon. Euclidean rotations and Loren
and thus longitudinally polarised nucleons cannot be converted in transve
infinite momentum. Only in case of non-relativistic quarks both distributi
Another difference emerges from an analysis of helicity amplitudes
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0)
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleo
emission of the quark (l0) by the nucleon (Λ0). Due to conservation of
parity, AΛlΛ0l0 = A Λ l Λ0 l0 and time reversal there are exactly three i
A++,++, A+ ,+ A+ , +.
The optical theorem relates the forward quark-nucleon scattering amplitu7
in helicity basis
helicity flip!
G
q
q
q
G
Transversity distribution
Transversity is chiral-odd!

8. Francesca Giordano
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin ei
transversity distribution hq
1 (x) measures the difference of the number de
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is ill
Differences between the helicity and transversity distributions are a con
motion of the quarks within the nucleon. Euclidean rotations and Loren
and thus longitudinally polarised nucleons cannot be converted in transve
infinite momentum. Only in case of non-relativistic quarks both distributi
Another difference emerges from an analysis of helicity amplitudes
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0)
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleo
emission of the quark (l0) by the nucleon (Λ0). Due to conservation of
parity, AΛlΛ0l0 = A Λ l Λ0 l0 and time reversal there are exactly three i
A++,++, A+ ,+ A+ , +.
The optical theorem relates the forward quark-nucleon scattering amplitu8
in helicity basis
G
q
q
q
G
Transversity distribution
helicity flip!
Transversity is chiral-odd!

9. Francesca Giordano
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin ei
transversity distribution hq
1 (x) measures the difference of the number de
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is ill
Differences between the helicity and transversity distributions are a con
motion of the quarks within the nucleon. Euclidean rotations and Loren
and thus longitudinally polarised nucleons cannot be converted in transve
infinite momentum. Only in case of non-relativistic quarks both distributi
Another difference emerges from an analysis of helicity amplitudes
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0)
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleo
emission of the quark (l0) by the nucleon (Λ0). Due to conservation of
parity, AΛlΛ0l0 = A Λ l Λ0 l0 and time reversal there are exactly three i
A++,++, A+ ,+ A+ , +.
The optical theorem relates the forward quark-nucleon scattering amplitu9
in helicity basis
G
q
q
q
G
Transversity distribution
helicity flip!
Transversity is chiral-odd!

10. Francesca Giordano
f q
1 (x) = q
!)
(x)+q
!(
(x).
Transversely polarised nucleons In the basis of transverse spin ei
transversity distribution hq
1 (x) measures the difference of the number de
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x).
The probabilistic interpretation of these parton distribution functions is ill
Differences between the helicity and transversity distributions are a con
motion of the quarks within the nucleon. Euclidean rotations and Loren
and thus longitudinally polarised nucleons cannot be converted in transve
infinite momentum. Only in case of non-relativistic quarks both distributi
Another difference emerges from an analysis of helicity amplitudes
scattering amplitudes AΛlΛ0l0 , labelled by the helicities of quarks (l(0)
(Λ(0) = ±1
2 ⌘ ±), represent the absorption of a quark (l) from a nucleo
emission of the quark (l0) by the nucleon (Λ0). Due to conservation of
parity, AΛlΛ0l0 = A Λ l Λ0 l0 and time reversal there are exactly three i
A++,++, A+ ,+ A+ , +.
The optical theorem relates the forward quark-nucleon scattering amplitu10
in helicity basis
G
q
q
q
G
(No gluon transversity
in the puzzle?)
Transversity distribution
helicity flip!
Transversity is chiral-odd!

11. Francesca Giordano 11
G
q
q
q
G
1. Can it be accessed? How?
Transversity is chiral-odd!
Yes! But only in conjunction with
another chiral-odd object
Transversity distribution
chiral oddchiral odd
}
chiral even observable
h1 x X
Accessible in different reactions
=> need of complementary reactions!

12. Francesca Giordano
Yes! But only in conjunction with
another chiral-odd object
12
Transversity distribution
G
q
q
q
G
2. Is transversity Universal?-> each reaction covers specific
kinematic ranges, and access specific
features
1. Can it be accessed? How?
Transversity is chiral-odd!
Accessible in different reactions
=> need of complementary reactions!

13. Francesca Giordano 13
G
q
q
q
G
3. How does transversity evolve?-> reactions are at different typical
energies
Yes! But only in conjunction with
another chiral-odd object
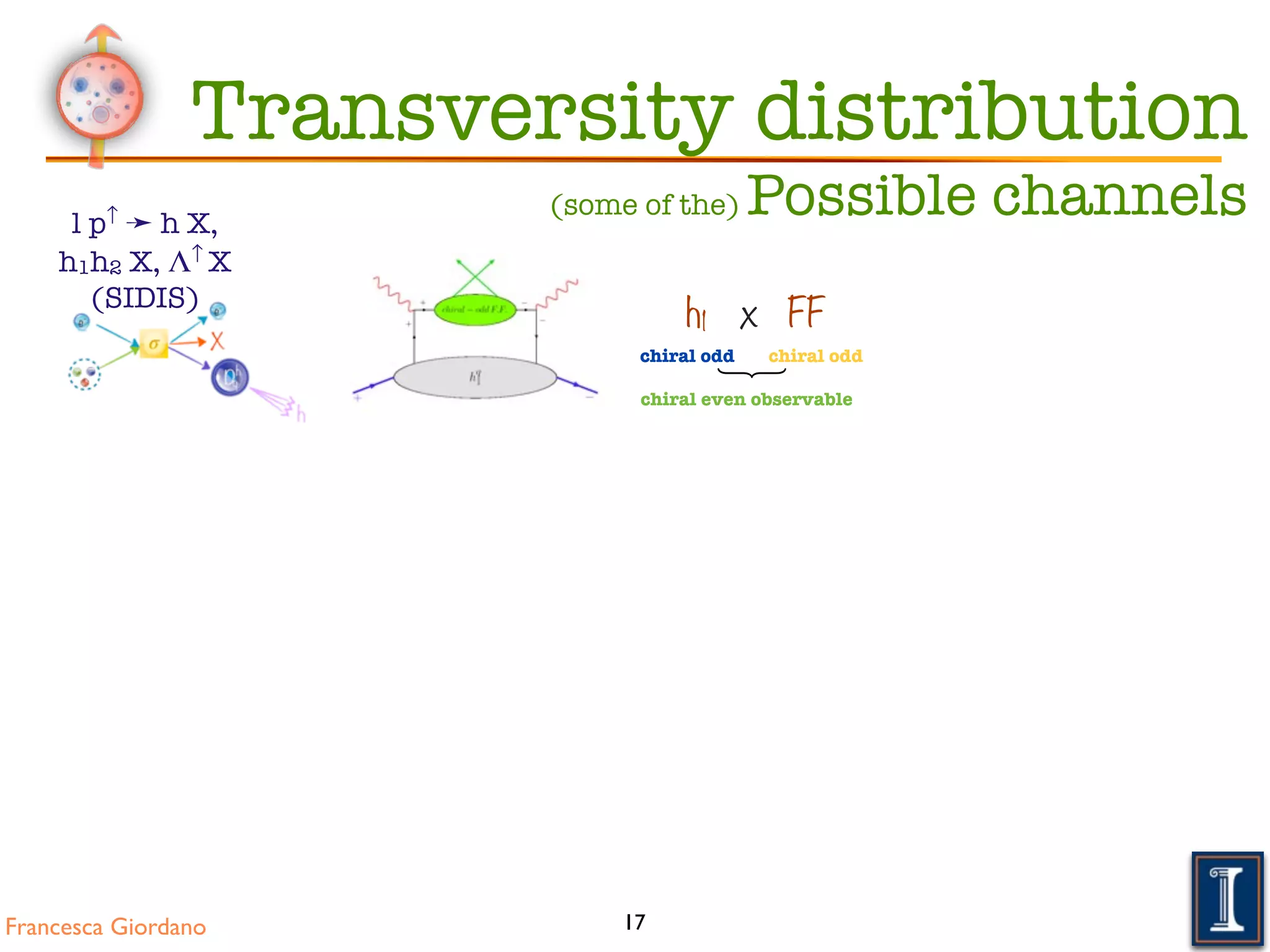
1. Can it be accessed? How?
Transversity is chiral-odd!
Transversity distribution
2. Is transversity Universal?-> each reaction covers specific
kinematic ranges, and access specific
features
Accessible in different reactions
=> need of complementary reactions!
ity distribution gq
1 (x) and the transversity distribution hq
1 (x) [RS79, AM90, JJ91]. Spin-depende
parton distribution functions can measured in polarised deep-inelastic scattering processes:
Longitudinally polarised nucleons The helicity distribution can be probed in deep-inelas
scattering of spin-polarised leptons off nucleons spin-polarised in directions longitudinal to the
coming leptons. The virtual photon, inheriting the lepton polarisation to a degree given by the lept
kinematics, can only interact with quarks polarised in opposite direction. This is a consequence
helicity conservation in the absorption of a spin-1 virtual photon by a spin-1
2 quark (g⇤q ! q). A
the virtual photon selects only quarks of one polarisation, measurements of the cross section f
anti-parallel (!() or parallel polarisations (!)) of lepton (!) and target nucleons ()) are sensiti
to number densities q of quarks polarised along or against the nucleon polarisation. In the infin
momentum frame, these number densities are related to the helicity distribution gq
1 (x), defined
the difference of the probability to find a quark polarised along or against the nucleon in a helic
eigenstate:
gq
1 (x) = q
!)
(x) q
!(
(x). (2.1
The momentum distribution measuring the spin average is given by the sum of these probabilities
f q
1 (x) = q
!)
(x)+q
!(
(x). (2.1
Transversely polarised nucleons In the basis of transverse spin eigenstates ("+ and "*), t
transversity distribution hq
1 (x) measures the difference of the number densities of transversely p
larised quarks aligned along or against the polarisation of the nucleon:
hq
1 (x) = q"*
(x) q"+
(x). (2.1
The probabilistic interpretation of these parton distribution functions is illustrated in table 2.1.
Differences between the helicity and transversity distributions are a consequence of the relativis
motion of the quarks within the nucleon. Euclidean rotations and Lorentz boosts do not commu
and thus longitudinally polarised nucleons cannot be converted in transversely polarised nucleons
infinite momentum. Only in case of non-relativistic quarks both distributions would be identical.
Another difference emerges from an analysis of helicity amplitudes. Forward quark-nucle
(0) 1
. Spin-orbit correlations in the nucleon
At leading twist (twist-two) three parton distribution functions characterise momentum and spin of
he quarks within the nucleon [Jaf97]. In addition to the momentum distribution f q
1 (x) 1, introduced
n the discussion of the parton model (section 2.1.2) , two spin-dependent functions appear: the helic-
y distribution gq
1 (x) and the transversity distribution hq
1 (x) [RS79, AM90, JJ91]. Spin-dependent
arton distribution functions can measured in polarised deep-inelastic scattering processes:
Longitudinally polarised nucleons The helicity distribution can be probed in deep-inelastic
cattering of spin-polarised leptons off nucleons spin-polarised in directions longitudinal to the in-
oming leptons. The virtual photon, inheriting the lepton polarisation to a degree given by the lepton
inematics, can only interact with quarks polarised in opposite direction. This is a consequence of
elicity conservation in the absorption of a spin-1 virtual photon by a spin-1
2 quark (g⇤q ! q). As
he virtual photon selects only quarks of one polarisation, measurements of the cross section for
nti-parallel (!() or parallel polarisations (!)) of lepton (!) and target nucleons ()) are sensitive
o number densities q of quarks polarised along or against the nucleon polarisation. In the infinite
momentum frame, these number densities are related to the helicity distribution gq
1 (x), defined as
he difference of the probability to find a quark polarised along or against the nucleon in a helicity
igenstate:
gq
1 (x) = q
!)
(x) q
!(
(x). (2.11)
The momentum distribution measuring the spin average is given by the sum of these probabilities:
f q
1 (x) = q
!)
(x)+q
!(
(x). (2.12)
Transversely polarised nucleons In the basis of transverse spin eigenstates ("+ and "*), the
ransversity distribution hq
1 (x) measures the difference of the number densities of transversely po-
arised quarks aligned along or against the polarisation of the nucleon:
~
?
No!

14. Francesca Giordano 14
G
q
q
q
G
no gluon transversity (in proton) and
quark and gluon transversities
don’t mix!
3. How does transversity evolve?-> reactions are at different typical
energies
Yes! But only in conjunction with
another chiral-odd object
1. Can it be accessed? How?
Transversity is chiral-odd!
Transversity distribution
2. Is transversity Universal?-> each reaction covers specific
kinematic ranges, and access specific
features
?
Accessible in different reactions
=> need of complementary reactions!

15. Francesca Giordano 15
G
q
q
q
G
no gluon transversity (in proton) and
quark and gluon transversities
don’t mix!
3. How does transversity evolve?-> reactions are at different typical
energies
Yes! But only in conjunction with
another chiral-odd object
1. Can it be accessed? How?
Transversity is chiral-odd!
Transversity distribution
2. Is transversity Universal?-> each reaction covers specific
kinematic ranges, and access specific
features
?
Accessible in different reactions
=> need of complementary reactions!

16. Francesca Giordano 16
Transversity distribution
(some of the) Possible channelsl p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

17. Francesca Giordano 17
chiral oddchiral odd
}
chiral even observable
h1 x FF
Transversity distribution
(some of the) Possible channelsl p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

18. Francesca Giordano 18
h1 x Collins
h1 x IFF
0h1 x FF
h1 x 𝛬FF
Transversity distribution
(some of the) Possible channelsl p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

19. Francesca Giordano 19
h1 x Collins
h1 x IFF
TMD0
Collinear
h1 x FF
h1 x 𝛬FF
Collinear
Transversity distribution
(some of the) Possible channelsl p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

20. Francesca Giordano
Transversity distribution
(some of the) Possible channels
20
f1 x h1 x FF
p p↑ ➛ h X,
h1h2 X, jets
h1 x Collins
h1 x IFF
TMD
FF
fq
1
0
Collinear
h1 x FF
f1 x h1 x Collins
f1 x h1 x IFF
0
Collinear
TMD
h1 x 𝛬FF
Collinear
l p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

21. Francesca Giordano 21
f1 x h1 x FF
h1 x Collins
h1 x IFF
TMD
FF
fq
1
0
Collinear
h1 x FF
f1 x h1 x Collins
f1 x h1 x IFF
0
Collinear
TMD
Transversity distribution
(some of the) Possible channels
h1 x 𝛬FF
p↑ h↑ ➛ (q↑ q↑➛)l+l-
(Fully polarized
Drell-Yan)
h1 x h1 Collinear
Collinear
p p↑ ➛ h X,
h1h2 X, jets
l p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)

22. Francesca Giordano
Transversity distribution
(some of the) Possible channels
22
They all access transversity via
single or double spin
asymmetries, f.i.:
AUT∝
AUT∝
ATT∝
How well do we know the unpolarized
cross-sections? In particular the TMD
unpolarized ones?
PT∝
h1 x Collins
h1 x IFF
TMD
Collinear
Collinear
0
h1 x 𝛬FF
p p↑ ➛ h X,
h1h2 X, jets f1 x h1 x Collins
f1 x h1 x IFF
0
Collinear
TMDAN∝
AN∝
h1 x h1
Collinear
p↑ h↑ ➛ (q↑ q↑➛)l+l-
(Fully polarized
Drell-Yan)
l p↑ ➛ h X,
h1h2 X, Λ↑ X
(SIDIS)
AUT =
" #
" + #

23. Francesca Giordano
H1
⊥
q
Ph⊥
Ph⊥
Collins
FF
23
Transversity distribution
First access in SIDIS
Interference
FF
Collinear
AUT∝ h1 x H1
⊥
0
AUT∝ h1 x H1
⪦
H1
⪦q
Ph⊥
Ph⊥
Transversity coupled with a
Fragmentation Function (FF)
TMD

24. Francesca Giordano
H1
⊥
q
Ph⊥
Ph⊥
Collins
FF
24
Transversity distribution
First access in SIDIS
Interference
FF
Collinear
AUT∝ h1 x H1
⊥
0
AUT∝ h1 x H1
⪦
H1
⪦q
Ph⊥
Ph⊥
Transversity coupled with a
Fragmentation Function (FF)
TMD
∫ h1 (x,pT) H1 (x,kT) dpT dkT
⊥
(and same in the denominator for
the unpolarized pdfs and ffs)
direct product!
(same in the denominator)

25. Francesca Giordano
AUT∝ h1 x H1
⊥
0
25
Transversity distribution
First access in SIDIS
Collins
FF
Transversity coupled with a
Fragmentation Function (FF)
TMD
Complementary reactions
TMD factorization assumed
FF universality assumed
M. Anselmino et al.,
PRD75:054032, 2007

26. Francesca Giordano
AUT∝ h1 x H1
⊥
0
26
Transversity distribution
First access in SIDIS
Collins
FF
Transversity coupled with a
Fragmentation Function (FF)
TMD
Very different energies between
Hermes/Compass and Belle:
Is TMD evolution different from
Collinear?
Complementary reactions
Collinear evolution assumed
TMD factorization assumed
FF universality assumed
M. Anselmino et al.,
PRD75:054032, 2007

27. Francesca Giordano
AUT∝ h1 x H1
⊥
0
27
Transversity distribution
First access in SIDIS
Collins
FF
Transversity coupled with a
Fragmentation Function (FF)
TMD
Very different energies between
Hermes/Compass and Belle:
Is TMD evolution different from
Collinear?
Different energies at Hermes/
Compass: how does transversity
evolve?
Complementary reactions
Collinear evolution assumed
No evolution assumed
TMD factorization assumed
FF universality assumed
M. Anselmino et al.,
PRD75:054032, 2007

28. Francesca Giordano
AUT∝ h1 x H1
⊥
0
28
Transversity distribution
First access in SIDIS
Collins
FF
Transversity coupled with a
Fragmentation Function (FF)
TMD
Very different energies between
Hermes/Compass and Belle:
Is TMD evolution different from
Collinear?
Different energies at Hermes/
Compass: how does transversity
evolve?Which is the TMD transversity and the TMD
Collins pT dependence? And the unpolarized
TMD pT dependence?
Complementary reactions
Collinear evolution assumed
No evolution assumed
TMD factorization assumed
Gaussian pT dependence assumed
FF universality assumed
M. Anselmino et al.,
PRD75:054032, 2007

29. Francesca Giordano
AUT∝ h1 x H1
⊥
0
29
Transversity distribution
First access in SIDIS
Collins
FF
Transversity coupled with a
Fragmentation Function (FF)
TMD
Complementary reactions
Collinear evolution assumed
No transversity evolution assumed
Transversity from Proton data
Transversity from pion pair production SIDIS off transversely polarized tar
Band:
1
100
1
10
0
0.2
0.4
x
x h1
uv
x x h1
dv
x 4
5%
• from COMPASS data
• DiFF analysis
• from BELLE data
• f1(x) from MSTW
• new analysis
1
100
1
10
0
0.2
0.4
x
x h1
uv
x x h1
dv
x 4
• from HERMES data
• DiFF analysis
• from BELLE data
• f1(x) from MSTW
• PRL107 & arXiv:1202.0323
1
100
1
10
0
0.2
0.4
x
x h1
uv
x x h1
dv
x 4
11%
Transversity from P
Transversity from pion pair
• from COMPASS data
• DiFF analysis
• from HERMES data
• DiFF analysis
• from BELLE data
• f1(x) from MSTW
• PRL107 & arXiv:1202.0323
Transversity from
Transversity from pion pa
• from COMPASS data
• DiFF analysis
• from BELLE data
• f1(x) from MSTW
• new analysis
• from HERMES data
• DiFF analysis
• from BELLE data
• f1(x) from MSTW
• PRL107 & arXiv:1202.0323
Bacchetta, Radici, Courtoy Phys.Rev.Lett.
107:012001,2011
Interference
FF
AUT∝ h1 x H1
⪦
Collinear
Transversity and Collins Gaussian pT
dependence assumed
TMD factorization assumed
FF universality assumed

30. Francesca Giordano 30
Transversity distribution
Access in pp
X
𝜎
Dq
h
h
AN∝ f1 x h1 x H1
⊥
00
Single hadron
But! the asymmetry for single
hadron comes mixed with other
effects (Sivers, higher twist)TMD
AN∝ f1 x h1 x H1
⪦

31. Francesca Giordano 31
Transversity distribution
Access in pp
X
𝜎
Dq
h
h
Jets
Single hadron
Looking at the hadron
distribution within the jet
TMD
AN∝ f1 x h1 x H1
⊥
00
AN∝ f1 x h1 x H1
⪦

32. Francesca Giordano 32
Transversity distribution
Access in pp
X
𝜎
Dq
h
h
Jets
Single hadron
TMD
Word of caution: TMD factorization
broken in pp➛hadrons
AN∝ f1 x h1 x H1
⪦
AN∝ f1 x h1 x H1
⊥
00

33. Francesca Giordano 33
Transversity distribution
Access in pp
X
𝜎
Dq
h
h
Jets
Single hadron
TMD
Collinear!
AN∝ f1 x h1 x H1
⊥
00
AN∝ f1 x h1 x H1
⪦

34. Francesca Giordano 34
Transversity distribution
Access in fully polarized Drell-Yan
Double Spin asymmetry:
ATT∝ h1 x h1 Cleanest theoretical access:
➛ no input needed for fragmentation functions
➛ Collinear case
To enhance the signal both quark and anti-quark
should come from the valence region
- medium-high x region
- preferable beam/target combination, f.i.:
proton/anti-proton (PAX, GSI) pion/proton (COMPASS, CERN)

35. Francesca Giordano 35
Double Spin asymmetry:
ATT∝ h1 x h1 Cleanest theoretical access:
➛ no input needed for fragmentation functions
➛ Collinear case
But experimentally challenging:
➛ low cross-section
➛ background cleaning
➛ anti-proton polarization still not proven to work
To enhance the signal both quark and anti-quark
should come from the valence region
- medium-high x region
- preferable beam/target combination, f.i.:
proton/anti-proton (PAX, GSI) pion/proton (COMPASS, CERN)
Transversity distribution
Access in fully polarized Drell-Yan

36. Francesca Giordano
pp IFF medium x high-x, precise Inclusion in
measurements global analysis
pp->jets Collins medium x high-x, precise TMD Evolution,
measurements TMD factorization
breaking
SIDIS Collins medium x high x TMD Evolution
measurement of (un)polarized
pdfs and FF pT dependence
SIDIS IFF medium x high x
Present Status
36
experimental
input needed
Drell-Yan no data! precise
measurements!
Jlab: Hall A&B
STAR
STAR
theoretical input
needed

37. Francesca Giordano
pp IFF medium x high-x, precise Inclusion in
measurements global analysis
pp->jets Collins medium x high-x, precise TMD Evolution,
measurements TMD factorization
breaking
SIDIS Collins medium x high x TMD Evolution
measurement of (un)polarized
pdfs and FF pT dependence
SIDIS IFF medium x high x
Present Status
37
experimental
input needed
Drell-Yan no data! precise
measurements!
Jlab: Hall A&B
STAR
STAR
theoretical input
needed
SuperStar
fsPHENIX
EIC
Jlab12
Jlab12
Babar
Belle/BelleII
SuperStar
fsPHENIX
COMPASSII
FERMILAB
PAX?
Star
Star

38. ... not there yet ...
38

39. ... but we took a few
feathers off ...
39

40. ... and planning new
experiments ...
40

41. Stay tuned!
41
Thank you!