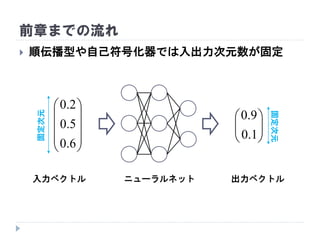
Recommended
PDF
(文献紹介)Deep Unrolling: Learned ISTA (LISTA)
PPTX
【DL輪読会】The Forward-Forward Algorithm: Some Preliminary
PDF
[DL輪読会]`強化学習のための状態表現学習 -より良い「世界モデル」の獲得に向けて-
PPTX
PPTX
【DL輪読会】Hopfield network 関連研究について
PPTX
猫でも分かるVariational AutoEncoder
PDF
PDF
PDF
PDF
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem...
PDF
【DL輪読会】StyleGAN-T: Unlocking the Power of GANs for Fast Large-Scale Text-to-I...
PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial)
PDF
Cosine Based Softmax による Metric Learning が上手くいく理由
PPTX
近年のHierarchical Vision Transformer
PPTX
【DL輪読会】WIRE: Wavelet Implicit Neural Representations
PPTX
強化学習エージェントの内発的動機付けによる探索とその応用(第4回 統計・機械学習若手シンポジウム 招待公演)
PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning
PDF
PDF
PDF
PDF
Layer Normalization@NIPS+読み会・関西
PDF
モデルアーキテクチャ観点からのDeep Neural Network高速化
PPTX
PDF
Skip Connection まとめ(Neural Network)
PDF
PDF
PDF
PDF
PDF
PDF
More Related Content
PDF
(文献紹介)Deep Unrolling: Learned ISTA (LISTA)
PPTX
【DL輪読会】The Forward-Forward Algorithm: Some Preliminary
PDF
[DL輪読会]`強化学習のための状態表現学習 -より良い「世界モデル」の獲得に向けて-
PPTX
PPTX
【DL輪読会】Hopfield network 関連研究について
PPTX
猫でも分かるVariational AutoEncoder
PDF
PDF
What's hot
PDF
PDF
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem...
PDF
【DL輪読会】StyleGAN-T: Unlocking the Power of GANs for Fast Large-Scale Text-to-I...
PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial)
PDF
Cosine Based Softmax による Metric Learning が上手くいく理由
PPTX
近年のHierarchical Vision Transformer
PPTX
【DL輪読会】WIRE: Wavelet Implicit Neural Representations
PPTX
強化学習エージェントの内発的動機付けによる探索とその応用(第4回 統計・機械学習若手シンポジウム 招待公演)
PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning
PDF
PDF
PDF
PDF
Layer Normalization@NIPS+読み会・関西
PDF
モデルアーキテクチャ観点からのDeep Neural Network高速化
PPTX
PDF
Skip Connection まとめ(Neural Network)
PDF
PDF
PDF
PDF
Viewers also liked
PDF
PDF
PDF
LSTM (Long short-term memory) 概要
PDF
Recurrent Neural Networks
PDF
PDF
PDF
AIによる働き方改革!~本当にストレスを感じている社員を見逃すな~
PDF
PDF
ReNom User Group #1 Part2
PDF
元BIエバンジェリストが語る!脱獄matplot!
PDF
~チュートリアル第1弾~ チュートリアルの概要と事例の紹介
PDF
楽しく使おう・始めよう!Raspberry Pi入門〜実践編〜
PDF
Binarized Neural Networks
PPT
PDF
ReNom User Group #1 Part3
PDF
[Dl輪読会]video pixel networks
PDF
ReNomによるNeural Style Transfer
PDF
ReNom User Group #1 Part1
PDF
PDF
これから Raspberry Pi をいじる方向けの資料 20130616版
Similar to 再帰型ニューラルネット in 機械学習プロフェッショナルシリーズ輪読会
PDF
[DL輪読会]Convolutional Conditional Neural Processesと Neural Processes Familyの紹介
PPTX
PPTX
Long short-term memory (LSTM)
PDF
PDF
深層学習(岡本孝之 著) - Deep Learning chap.1 and 2
PPTX
PDF
PPT
PDF
東京都市大学 データ解析入門 10 ニューラルネットワークと深層学習 1
PDF
Nested RNSを用いたディープニューラルネットワークのFPGA実装
PDF
PDF
Scikit-learn and TensorFlow Chap-14 RNN (v1.1)
PPTX
「機械学習とは?」から始める Deep learning実践入門
PPTX
PDF
PPTX
PDF
DOCX
PDF
PDF
More from Shotaro Sano
PDF
ディリクレ過程に基づく無限混合線形回帰モデル in 機械学習プロフェッショナルシリーズ輪読会
PDF
Microsoft Malware Classification Challenge 上位手法の紹介 (in Kaggle Study Meetup)
PDF
サポートベクトルデータ記述法による異常検知 in 機械学習プロフェッショナルシリーズ輪読会
PDF
PDF
PDF
PFDet: 2nd Place Solutions to Open Images Competition
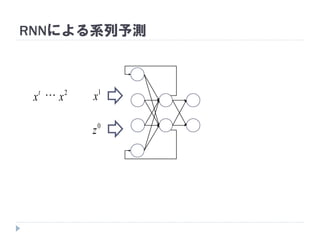
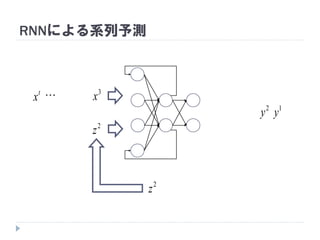
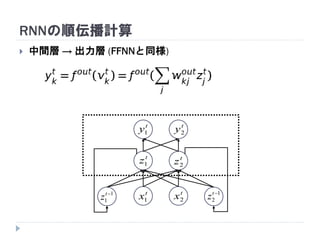
再帰型ニューラルネット in 機械学習プロフェッショナルシリーズ輪読会 1. 2. 3. 4. 応用
自然言語処理
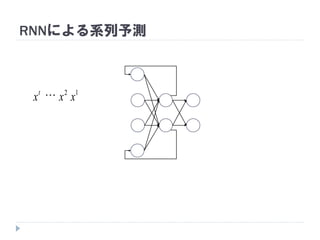
途中までの文章から次の単語を順次予測
音声認識
短時間フレーム毎の音素認識
We can get an idea of the quality of the leaned feature
1
x 2
x 3
x 4
x 5
x 6
x 7
x 8
x 9
x 10
x 11
x
11
y
w ʌ n n nʌʌʌʌww
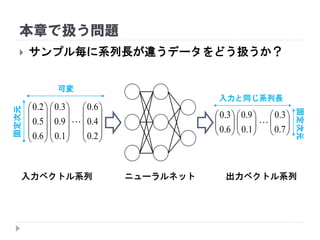
5. トピック
Recurrent Neural Network (RNN)
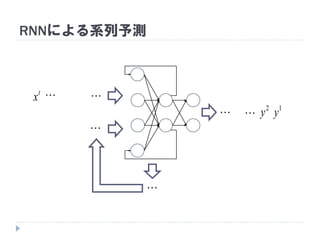
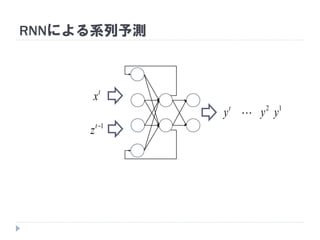
系列量が異なるサンプルの予測・学習
Long Short-Term Memory (LSTM)
より長い系列の予測・学習
Connectionist Temporal Classification (CTC)
時間フレーム単位のラベル付けが不要なRNN学習
6. 略語
FFNN
Feed Forward Neural Network
順伝播型ニューラルネットワーク
RNN
Recurrent Neural Network
再帰型ニューラルネットワーク
BP
Back Propagation
誤差逆伝播法
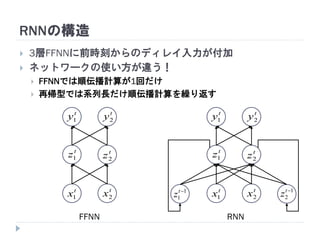
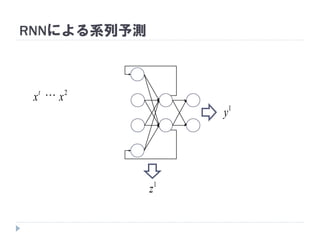
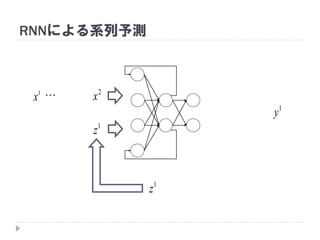
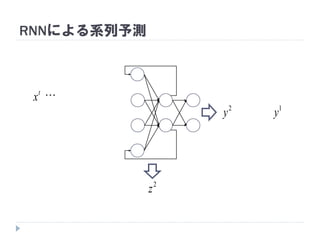
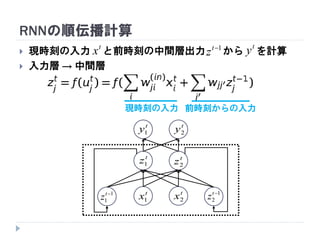
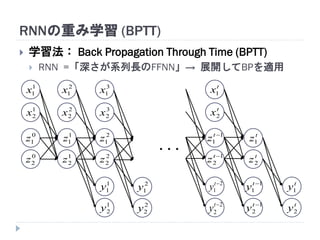
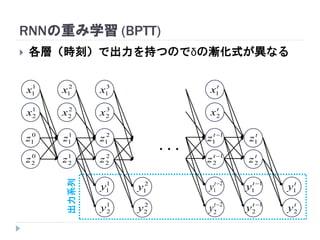
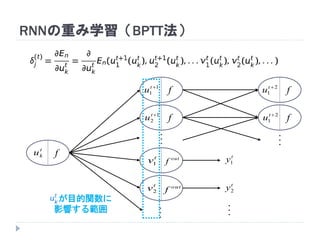
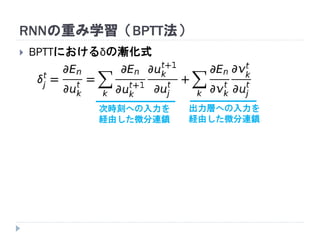
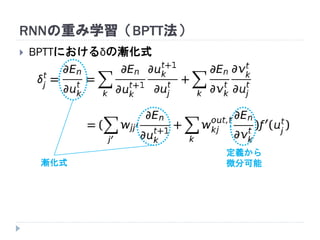
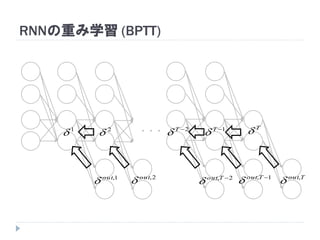
7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. RNNの重み学習 (BPTT)
学習法: Back Propagation Through Time (BPTT)
RNN =「深さが系列長のFFNN」→ 展開してBPを適用
1
1x
1
2x
0
1z
0
2z
2
1x
2
2x
1
1z
1
2z
3
1x
3
2x
2
1z
2
2z
1
1y
1
2y
t
x1
t
x2
1
1
t
z
1
2
t
z
2
1
t
y
2
2
t
y
2
1y
2
2y
t
y1
t
y2
t
z1
t
z2
1
1
t
y
1
2
t
y
・・・
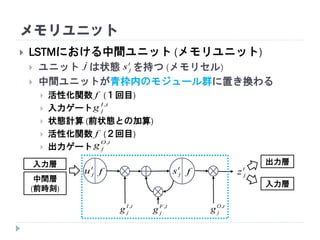
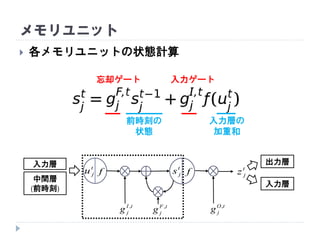
20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. LSTMにおける中間ユニット (メモリユニット)
ユニット は状態 を持つ (メモリセル)
中間ユニットが青枠内のモジュール群に置き換わる
活性化関数 (1回目)
入力ゲート
状態計算 (前状態との加算)
活性化関数 (2回目)
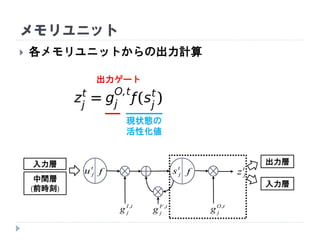
出力ゲート
メモリユニット
入力層 出力層
入力層
t
ju t
jz
t
jsf f
tI
jg ,
tO
jg ,
f
f
t
jsj
中間層
(前時刻)
tI
jg , tF
jg , tO
jg ,
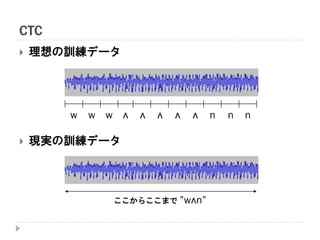
36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. CTC
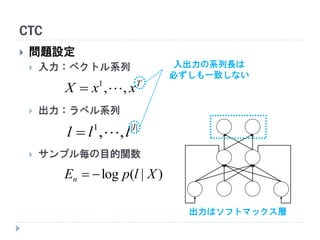
問題設定
入力:ベクトル系列
出力:ラベル系列
サンプル毎の目的関数
T
xxX ,,1
||1
,, l
lll
)|(log XlpEn
入出力の系列長は
必ずしも一致しない
出力はソフトマックス層
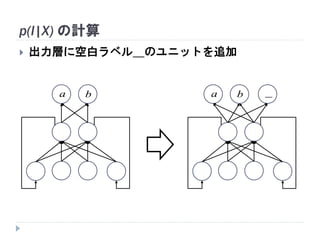
49. 50. 51. 52. p(l|X) の計算
入出力の系列長を揃えたい
空白ラベル_が存在すると仮定
各正解ラベルを(空白ラベルor同じラベル)の連続で埋める
""abl
__,_,_,,,ba
__,_,,,, baa
ba _,_,_,_,,
bbbaaa ,,,,,
系列長6の場合
RNNからの出力ラベルは
この中のどれか
(確率的にしか分からない)
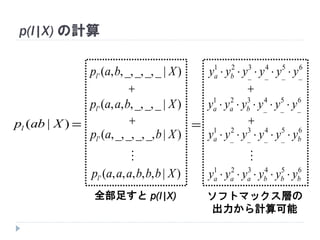
53. p(l|X) の計算
)|( Xabpl
)|__,_,_,,,(' Xbapl
)|__,_,,,,(' Xbaapl
)|_,_,_,_,,(' Xbapl
)|,,,,,(' Xbbbaaapl
全部足すと p(l|X)
6
_
5
_
4
_
3
_
21
yyyyyy ba
6
_
5
_
4
_
321
yyyyyy baa
65
_
4
_
3
_
2
_
1
ba yyyyyy
654321
bbbaaa yyyyyy
ソフトマックス層の
出力から計算可能
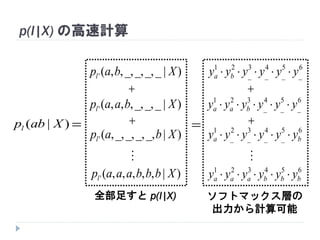
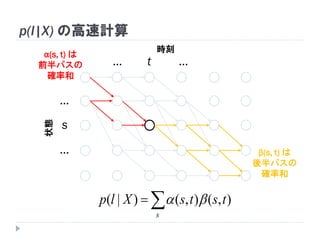
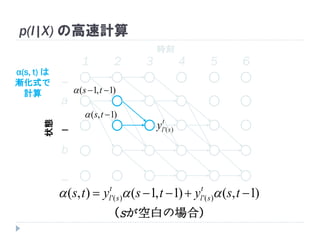
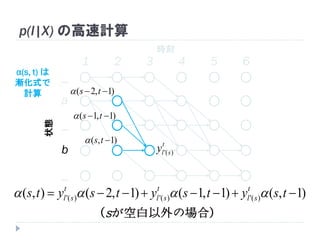
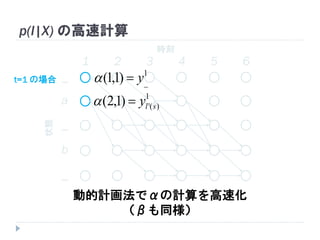
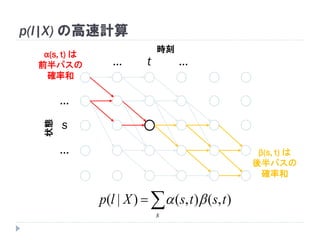
54. 55. p(l|X) の高速計算
)|( Xabpl
)|__,_,_,,,(' Xbapl
)|__,_,,,,(' Xbaapl
)|_,_,_,_,,(' Xbapl
)|,,,,,(' Xbbbaaapl
全部足すと p(l|X)
6
_
5
_
4
_
3
_
21
yyyyyy ba
6
_
5
_
4
_
321
yyyyyy baa
65
_
4
_
3
_
2
_
1
ba yyyyyy
654321
bbbaaa yyyyyy
ソフトマックス層の
出力から計算可能
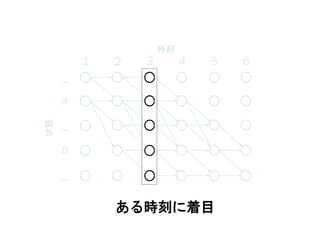
56. 1 2 3 4 5 6
時刻状態
_
a
_
b
_
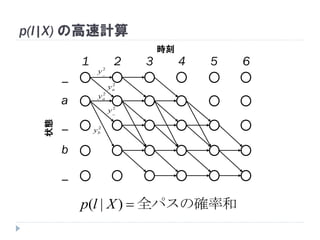
p(l|X) の高速計算
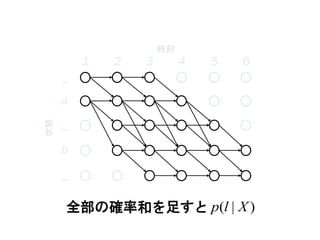
全パスの確率和)|( Xlp
2
_y
2
ay
2
ay
2
by
2
_y
57. 1 2 3 4 5 6
時刻状態
ある時刻に着目
_
a
_
b
_
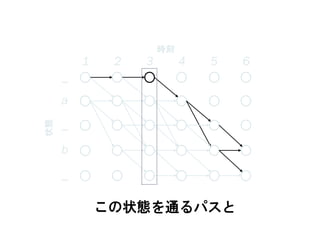
58. 1 2 3 4 5 6
時刻状態
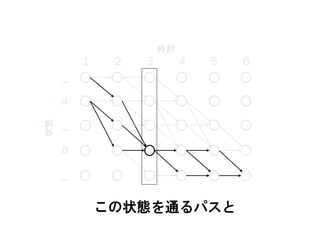
この状態を通るパスと
_
a
_
b
_
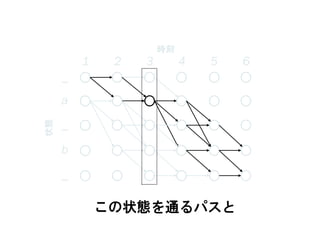
59. 1 2 3 4 5 6
時刻状態
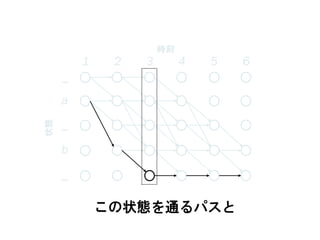
この状態を通るパスと
_
a
_
b
_
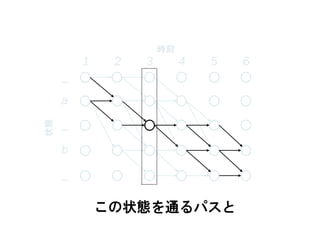
60. 1 2 3 4 5 6
時刻状態
この状態を通るパスと
_
a
_
b
_
61. 1 2 3 4 5 6
時刻状態
この状態を通るパスと
_
a
_
b
_
62. 1 2 3 4 5 6
時刻状態
この状態を通るパスと
_
a
_
b
_
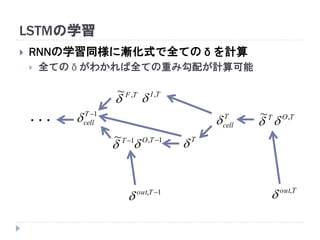
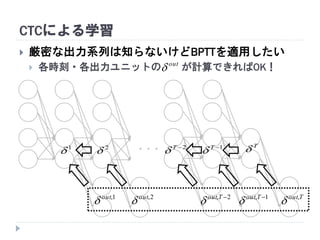
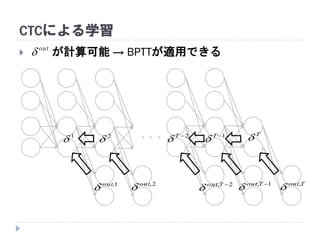
63. 64. 65. 66. 67. 68. 69. 70. 71. 72. CTCによる学習
が計算可能 → BPTTが適用できる
・・・
T
1, Tout
1T
2, Tout
2T
1
2
2,out
1,out
Tout,
out
73. 74.