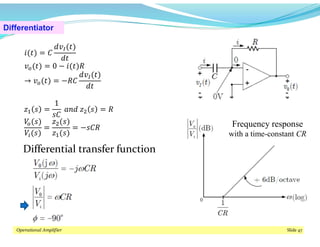
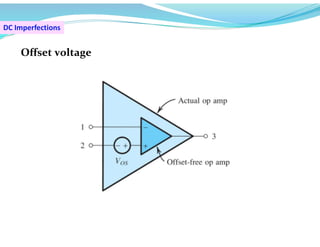
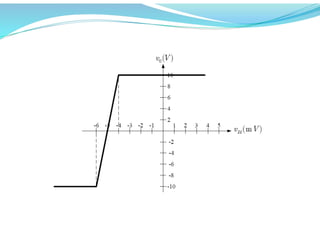
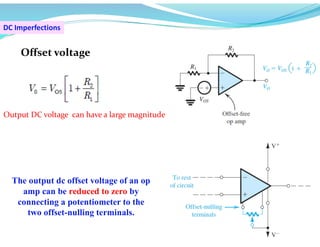
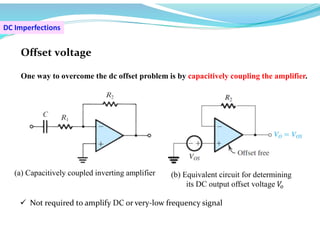
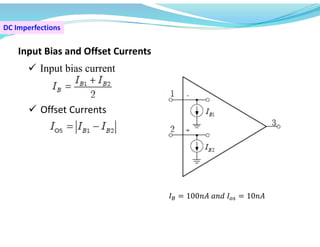
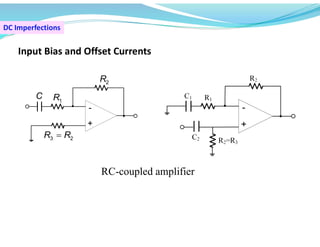
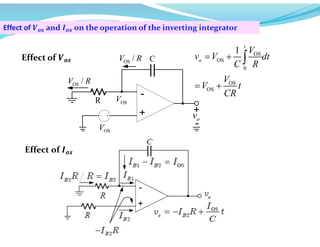
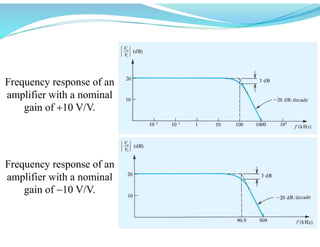
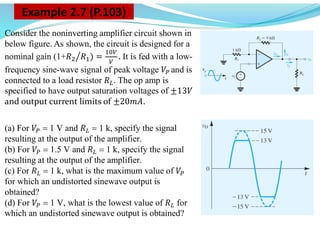
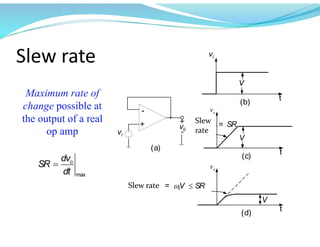
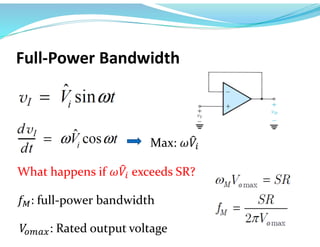
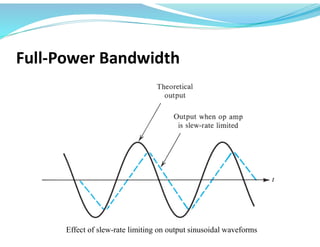
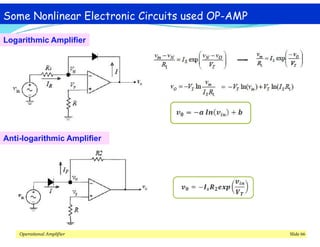
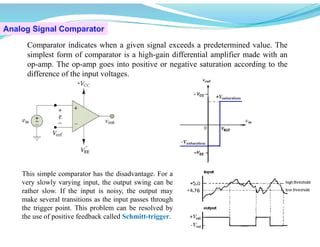
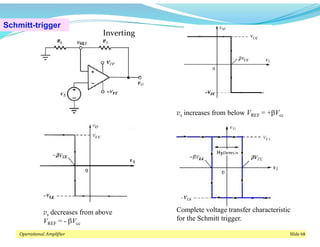
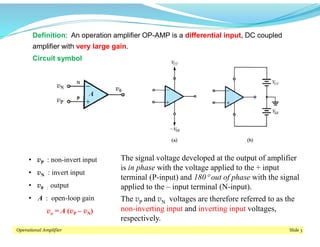
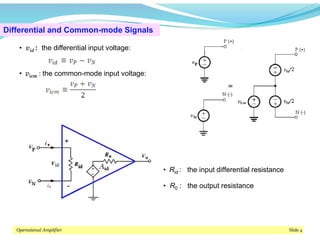
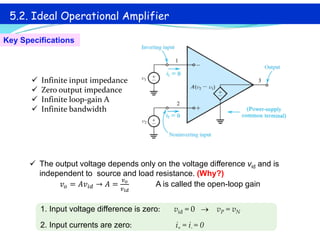
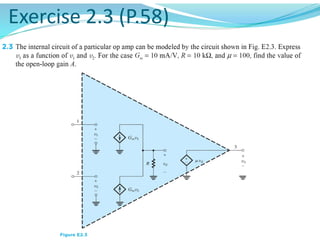
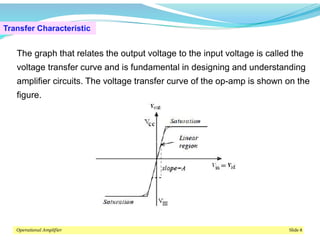
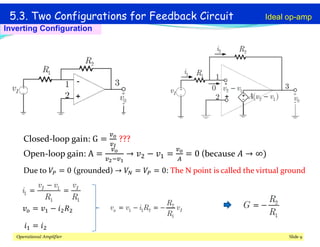
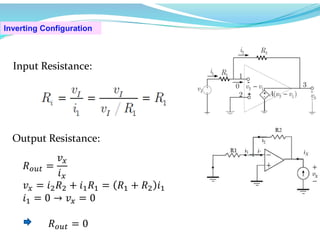
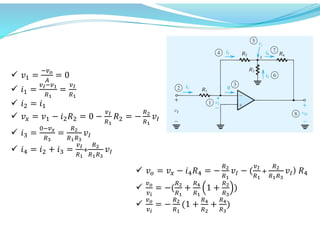
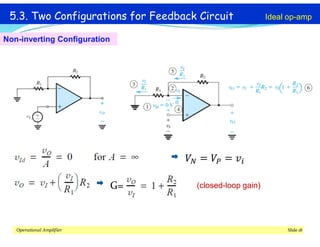
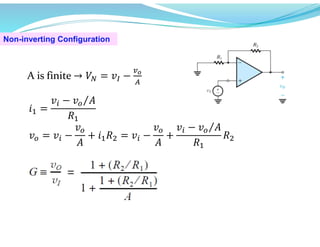
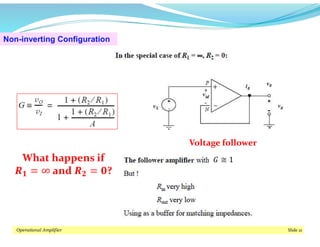
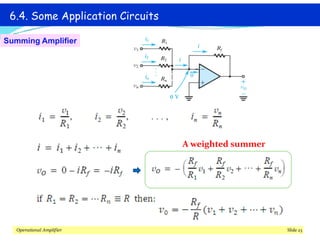
This document discusses operational amplifiers (op-amps), outlining their definitions, configurations, and ideal characteristics. Op-amps serve as fundamental components in various electronic circuits, demonstrating significant application in both analog computers and modern devices. The content further elaborates on inverting and non-inverting configurations, gain specifications, and imperfections such as offset voltage and input bias currents.

1. Chapter 1
Operational Amplifier and
Application Circuits
Slide 1

2. • An Operational amplifier ("op-amp") is a DC-coupled high-gain electronic
voltage amplifier with a differential input and, usually, a single-ended
output.
• An op-amp produces an output voltage that is typically hundreds of
thousands times larger than the voltage difference between its input
terminals.
• Operational amplifiers are important building blocks for a wide range of
electronic circuits. They had their origins in analog computers where they
were used in many linear, non-linear and frequency-dependent circuits
(summation, integration, …).
• Op-amps are among the most widely used electronic devices today,
being used in a vast array of consumer, industrial, and scientific devices.
• The op-amp is one type of differential amplifier.
5.1. Introduction
Definition and Notation of Operational Amplifier (op-amp)

3. Operational Amplifier Slide 3
Definition: An operation amplifier OP-AMP is a differential input, DC coupled
amplifier with very large gain.
The signal voltage developed at the output of amplifier
is in phase with the voltage applied to the + input
terminal (P-input) and 180 out of phase with the signal
applied to the – input terminal (N-input).
The vP and vN voltages are therefore referred to as the
non-inverting input and inverting input voltages,
respectively.
• vP : non-invert input
• vN : invert input
• v0 : output
• A : open-loop gain
vo = A (vP – vN)
Circuit symbol

4. Differential and Common-mode Signals
• Rid : the input differential resistance
• R0 : the output resistance
• vid : the differential input voltage:
• vicm : the common-mode input voltage:
Operational Amplifier Slide 4

5. 5.2. Ideal Operational Amplifier
1. Input voltage difference is zero: vid = 0  vP = vN
2. Input currents are zero: i+ = i- = 0
Key Specifications
 Infinite input impedance
 Zero output impedance
 Infinite loop-gain A
 Infinite bandwidth
 The output voltage depends only on the voltage difference vid and is
independent to source and load resistance. (Why?)
𝑣 = 𝐴𝑣 → 𝐴 = A is called the open-loop gain

6. Exercise 2.2 (P.57)

7. Exercise 2.3 (P.58)

8. The graph that relates the output voltage to the input voltage is called the
voltage transfer curve and is fundamental in designing and understanding
amplifier circuits. The voltage transfer curve of the op-amp is shown on the
figure.
Transfer Characteristic
Operational Amplifier Slide 8

9. Operational Amplifier Slide 9
Inverting Configuration
5.3. Two Configurations for Feedback Circuit Ideal op-amp
Closed-loop gain: G = ???
Open-loop gain: A = → 𝑣 − 𝑣 = = 0 (because 𝐴 → ∞)
Due to 𝑉 = 0 (grounded) → 𝑉 = 𝑉 = 0: The N point is called the virtual ground
𝑖 = 𝑖
𝑣 = 𝑣 − 𝑖 𝑅

10. Inverting Configuration
(A is finite)
A is finite → 𝑉 = −
(If 𝐴 → ∞ then 𝐺 = −𝑅 𝑅
⁄ )
𝑣 − 𝑣 =
𝑣
𝐴
𝑣 = 0
𝑣 = −
𝑣
𝐴

11. Inverting Configuration
Input Resistance:
Output Resistance:
𝑅 =
𝑣
𝑖
𝑣 = 𝑖 𝑅 + 𝑖 𝑅 = 𝑅 + 𝑅 𝑖
𝑖 = 0 → 𝑣 = 0
𝑅 = 0

12. Example 2.1 (P.62)
Fig. 2.5

13. Example 2.2 (P.63)
Figure 2.8 Circuit for Example 2.2. The circled numbers indicate
the sequence of the steps in the analysis.

14.  𝑣 = = 0
 𝑖 = =
 𝑖 = 𝑖
 𝑣 = 𝑣 − 𝑖 𝑅 = 0 − 𝑅 = − 𝑣
 𝑖 = = 𝑣
 𝑖 = 𝑖 + 𝑖 = + 𝑣
 𝑣 = 𝑣 − 𝑖 𝑅 = − 𝑣 − ( + 𝑣 ) 𝑅
 = −( + 1 + )
 = − (1 + + )

15. Exercise D2.4 (P.65)
Figure 2.5 The inverting closed-loop configuration.

16. Exercise 2.5 (P.65)
𝑅 =
𝑣
𝑖

17. Exercise 2.6 (P.65)

18. Non-inverting Configuration
5.3. Two Configurations for Feedback Circuit Ideal op-amp
Operational Amplifier Slide 18
(closed-loop gain)
𝑉 = 𝑉 = 𝑣
G=

19. Non-inverting Configuration
A is finite → 𝑉 = 𝑣 −
𝑖 =
𝑣 − 𝑣 𝐴
⁄
𝑅
𝑣 = 𝑣 −
𝑣
𝐴
+ 𝑖 𝑅 = 𝑣 −
𝑣
𝐴
+
𝑣 − 𝑣 𝐴
⁄
𝑅
𝑅

20. Operational Amplifier Slide 20
Non-inverting Configuration

21. Operational Amplifier Slide 21
Non-inverting Configuration
𝐺 ≅ 1
Voltage follower
What happens if
𝑹𝟏 = ∞ and 𝑹𝟐 = 𝟎?

22. Exercise 2.13 (P.71)

23. Summing Amplifier
6.4. Some Application Circuits
Operational Amplifier Slide 23
A weighted summer

24. Summing Amplifier
A weighted summer capable of implementing
summing coefficients of both signs.

25. Exercise D2.7 (P.67)

26. Exercise 2.9 and 2.10 (P.70)

27. Difference Amplifiers
Common-mode rejection ration (CMRR)

28. Difference Amplifiers
𝑣 = 0 Inverting amplifier
𝑣 = 0 Non inverting amplifier
𝑣 ≠ 0 and 𝑣 ≠ 0
Note: we have to make the two
gain magnitudes equal in order
to reject common-mode signals

29. Difference Amplifiers
Note: we have to make the two gain magnitudes equal in order to reject
common-mode signals
Differential gain

30. Difference Amplifiers
Common – mode input signal
(note: 𝑖 = 𝑖 )
𝑣 = 0 → 𝐴 = 0
However, that any mismatch
in the resistance ratios can
make 𝑨𝒄𝒎 nonzero, and
hence CMRR finite.

31. Difference Amplifiers
Differential Input Resistance 𝑅

32. Exercise 2.15 (P.76)
(Eq.2.19)

33. Exercise D2.16

34. Instrumentation Amplifier
Due to the input resistance of the difference amplifier is too low, the instrumentation
amplifier should be used. It is a combination between 2 non-invert amplifiers and a
difference amplifier so that this scheme becomes a high-qualified amplifier.
𝑣 =
𝑣 =
Stage 1:
𝑣 = (1 +
𝑅
𝑅
)𝑣
𝑣 = (1 +
𝑅
𝑅
)𝑣

35. Instrumentation Amplifier
Stage 2:
𝑣 = (1 +
𝑅
𝑅
)𝑣
𝑣 = (1 +
𝑅
𝑅
)𝑣
𝑣 = 𝑣 − 𝑣
𝑣 =
𝑣 =
𝑣
𝑣
𝑣 = 1 +
𝑅
𝑅
𝑣 − 𝑣
𝑣 = 1 +
𝑅
𝑅
𝑣
𝑣 =
𝑅
𝑅
𝑣

36. Instrumentation Amplifier
Advantages:
 Very high (ideally infinite) input resistance
 High differential gain
Disadvantages:
 𝒗𝑰𝒄𝒎 is amplified in stage 1 by a gain equal to that
experienced by 𝑣 . This is a very serious issue, for it could
result in the signals at the outputs of A1 and A2 being of
such large magnitudes that the op amps saturate. But
even if the op amps do not saturate, the difference amplifier
of stage 2 will now have to deal with much larger common-
mode signals, with the result that the CMRR of the overall
amplifier will inevitably be reduced.

37. Instrumentation Amplifier
Disadvantages:
 The two amplifier channels in stage 1 have to be perfectly
matched, otherwise a spurious signal may appear between
their two outputs. Such a signal would get amplified by the
difference amplifier in the second stage.
 To vary the differential gain 𝐴 , two resistors 𝑅 have to be
varied simultaneously. At each gain setting the two
resistors have to be perfectly matched: a difficult task.

38. Instrumentation Amplifier

39. Example 2.3 (P.79)
Design the instrumentation amplifier circuit in the above to
provide a gain that can be varied over the range of 2 to 1000
utilizing a 100kvariable resistance (a potentiometer, or “pot” for
short).

41. Exercise 2.17
Fig.2.20

42. Integrators and Differentiators
The inverting configuration with general impedances
Closed-loop transfer function

43. Integrators
Operational Amplifier Slide 43
Miller or Inverting Integrator
𝑖 (𝑡) flows through the capacitor C,
causing charge to accumulate on C
equal to∫ 𝑖 (𝑡) 𝑑𝑡.
Capacitor voltage 𝑣 (𝑡) charges
by ∫ 𝑖 𝑡 𝑑𝑡.
where 𝑉 is initial voltage on C
Output voltage

44. Integrators
For physical frequencies, 𝑠 = 𝑗𝜔
And phase
Integrator frequency:
Frequency response
Magnitude of integrator transfer function
Low-pass filter

45. Integrators
Miller or Inverting Integrator with 𝑹𝑭
𝑖 =
𝑣
𝑅
𝑍 = 𝑅 ∥ 𝑠𝐶 =
𝑅
1 + 𝑅 𝑠𝐶
𝑣 = 0 − 𝑖 𝑍=-
⁄
𝑣

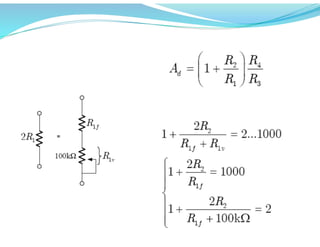
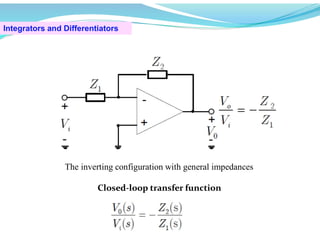
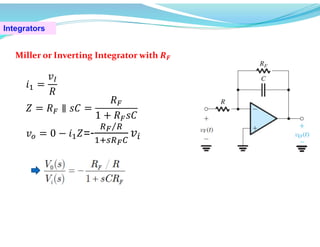
46. Example 2.5 (P.85)
Find the output produced by a Miller integrator in response to an
input pulse of 1-V height and 1-ms width [below figure]. Let
R10kand C 10nF. The op amp is specified to saturate at
± 13𝑉.

47. Differentiator
Operational Amplifier Slide 47
𝑖(𝑡) = 𝐶
𝑑𝑣 (𝑡)
𝑑𝑡
𝑣 (𝑡) = 0 − 𝑖(𝑡)𝑅
→ 𝑣 (𝑡) = −𝑅𝐶
𝑑𝑣 (𝑡)
𝑑𝑡
𝑧 𝑠 =
1
𝑠𝐶
𝑎𝑛𝑑 𝑧 𝑠 = 𝑅
𝑉 (𝑠)
𝑉 (𝑠)
=
𝑧 (𝑠)
𝑧 (𝑠)
= −𝑠𝐶𝑅
Differential transfer function
Frequency response
with a time-constant CR

48. DC Imperfections
Offset voltage

49. Exercise 2.21 (P.90)
Use the model at before slide to sketch the transfer characteristic
𝑣 versus 𝑣 (𝑣 ≡ 𝑣 and 𝑣 ≡ 𝑣 − 𝑣 of an op amp having
an open-loop dc gain 𝐴 = 10 V/V, output saturation levels of
± 10𝑉 and 𝑣 of +5mV.

51. DC Imperfections
Offset voltage
Output DC voltage can have a large magnitude
The output dc offset voltage of an op
amp can be reduced to zero by
connecting a potentiometer to the
two offset-nulling terminals.

52. DC Imperfections
Offset voltage
One way to overcome the dc offset problem is by capacitively coupling the amplifier.
(b) Equivalent circuit for determining
its DC output offset voltage 𝑉
(a) Capacitively coupled inverting amplifier
 Not required to amplify DC or very-low frequency signal

53. DC Imperfections
Input Bias and Offset Currents
 Offset Currents
 Input bias current
𝐼 = 100𝑛𝐴 𝑎𝑛𝑑 𝐼 = 10𝑛𝐴

54. DC Imperfections
Input Bias and Offset Currents
Reducing the effect of the input bias
currents by introducing a resistor R3
In case 𝐼 = 𝐼 = 𝐼
If Then 𝑉 = 0
The effect of the input bias currents is removed
Denote Minimize the effect of the
input bias currents

55. DC Imperfections
Input Bias and Offset Currents
2
R
1
R
3 2
R R

C
RC-coupled amplifier

56. Effect of 𝑽𝒐𝒔 and 𝑰𝒐𝒔 on the operation of the inverting integrator
OS
V
OS
V
OS /
V R
OS /
V R
o
v
OS
OS
0
OS
OS
1
t
o
V
v V dt
C R
V
V t
CR
 
 

Effect of 𝑽𝒐𝒔
Effect of 𝑰𝒐𝒔

57. Frequency Dependence of the Open-Loop Gain
where ω >> ωb
( )
1 /
(j )
1 /
o
b
o
b
A
A s
s
A
A
j


 




(j ) o b
o b
A
A
A



 


b
f t
f
or

58. Frequency Dependence of the Closed-Loop Gain
Closed – Loop Gain:
If 𝐴 ≫ 1 + 𝑅 𝑅
⁄
 
2 1
2 1
3dB
2 1
( ) /
( ) 1
/ 1 /
1 /
o
i
t
t
V s R R
s
V s
R R
R R










59. Example 2.6 (P.100)
Consider an op amp with ft 1 MHz. Find the 3-dB frequency
of closed-loop amplifiers with nominal gains of 1000, 100,
10, 1, 1, 10, 100, and 1000. Sketch the magnitude
frequency response for the amplifiers with closed-loop gains of
10 and –10.
3dB
2 1
1 /
t
R R

 


60. Frequency response of an
amplifier with a nominal
gain of 10 V/V.
Frequency response of an
amplifier with a nominal
gain of 10 V/V.

61. Large-Signal Operation of Op Amps
-
+
0
t
0
t
15V
13V
-15V
-13V
1 1
R k
 
2 9
R k
 
P
V
I
v
0
i
L
i
F
i
L
R
0
v
0
v
 Output Voltage Saturation
 Output Current Limits

62. Example 2.7 (P.103)
Consider the noninverting amplifier circuit shown in
below figure. As shown, the circuit is designed for a
nominal gain (1+𝑅 𝑅 ) = . It is fed with a low-
frequency sine-wave signal of peak voltage 𝑉 and is
connected to a load resistor 𝑅 . The op amp is
specified to have output saturation voltages of ±13𝑉
and output current limits of ±20𝑚𝐴.
(a) For 𝑉 1 V and 𝑅 1 kspecify the signal
resulting at the output of the amplifier.
(b) For 𝑉 1.5 V and 𝑅 1 k, specify the signal
resulting at the output of the amplifier.
(c) For 𝑅 1 k, what is the maximum value of 𝑉
for which an undistorted sinewave output is
obtained?
(d) For 𝑉 1 V, what is the lowest value of 𝑅 for
which an undistorted sinewave output is obtained?

63. Slew rate
max
o
dv
SR
dt

I
v
V
o
v
o
v
V
V
I
v 0
v
tV SR
 
SR
Slew rate
Slew
rate
Maximum rate of
change possible at
the output of a real
op amp

64. Full-Power Bandwidth
Max: 𝜔𝑉
What happens if 𝜔𝑉 exceeds SR?
𝑓 : full-power bandwidth
𝑉 : Rated output voltage

65. Full-Power Bandwidth
Effect of slew-rate limiting on output sinusoidal waveforms

66. Some Nonlinear Electronic Circuits used OP-AMP
Logarithmic Amplifier
Anti-logarithmic Amplifier
Operational Amplifier Slide 66

67. Analog Signal Comparator
Comparator indicates when a given signal exceeds a predetermined value. The
simplest form of comparator is a high-gain differential amplifier made with an
op-amp. The op-amp goes into positive or negative saturation according to the
difference of the input voltages.
This simple comparator has the disadvantage. For a
very slowly varying input, the output swing can be
rather slow. If the input is noisy, the output may
make several transitions as the input passes through
the trigger point. This problem can be resolved by
the use of positive feedback called Schmitt-trigger.

68. Schmitt-trigger
vs increases from below VREF = +Vcc
vs decreases from above
VREF = - Vcc
Complete voltage transfer characteristic
for the Schmitt trigger.
Operational Amplifier Slide 68
Inverting