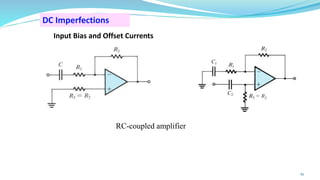
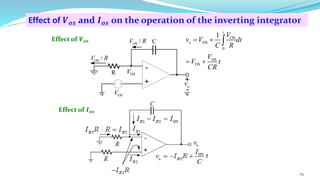
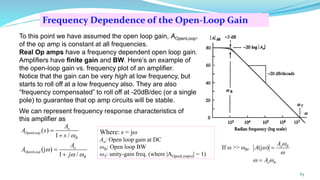
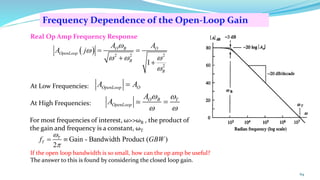
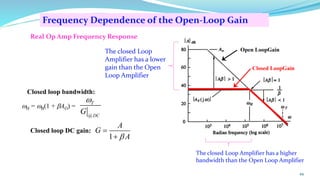
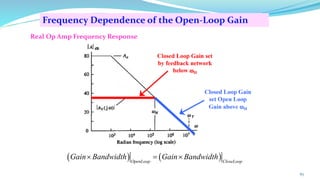
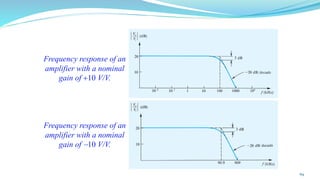
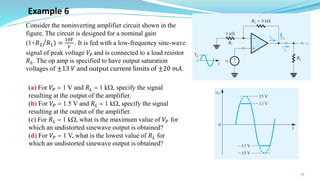
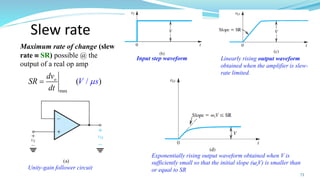
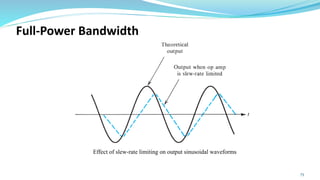
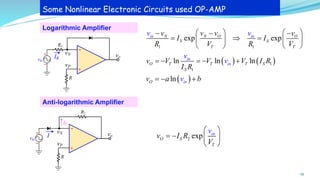
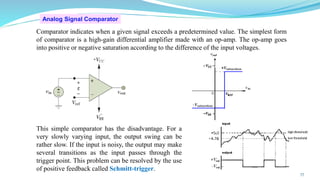
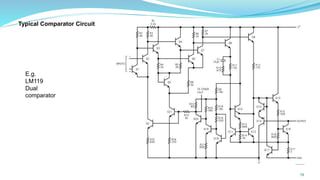
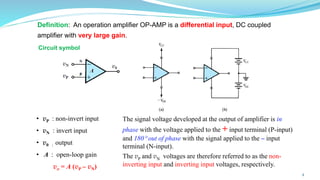
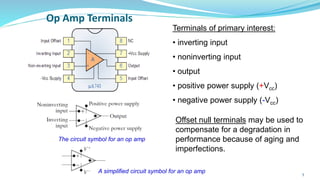
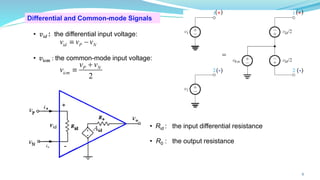
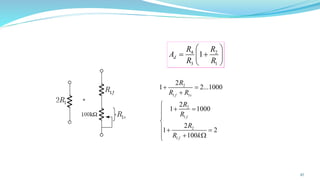
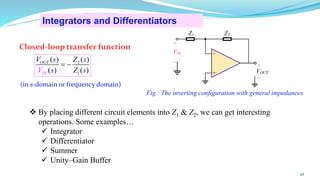
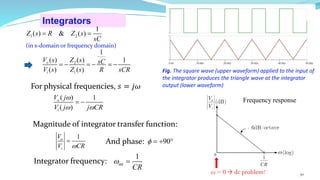
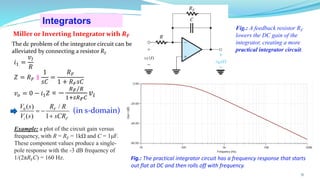
The document provides an in-depth overview of operational amplifiers (op-amps), including their definitions, characteristics, configurations, and applications in electronic circuits. Op-amps are high-gain differential amplifiers that can be used in various configurations for amplifying signals, filters, and buffering circuits. It also covers ideal and practical op-amps, emphasizing their performance traits and common applications such as inverting and non-inverting configurations.

1. Lecture #5
Operational Amplifier and
Application Circuits
CHAPTER 2, S&S text book
Mai Linh, PhD
Faculty of Electronics and Telecommunications,
VNU-University of Engineering and Technology
linhmai@vnu.edu.vn ; mlinh2009@gmail.com
1
Dual-in-line
package (DIP)
Surface mount:
small-outline
integrated
circuit (SOIC)
package
Plastic-leaded chip
carrier (PLCC)
package

2. • An Operational amplifier ("op-amp") is a DC-coupled high-gain electronic voltage amplifier with a
differential input and, usually, a single-ended output.
• An op-amp produces an output voltage that is typically hundreds of thousands times larger than
the voltage difference between its input terminals.
• Operational amplifiers are important building blocks for a wide range of electronic circuits.
They had their origins in analog computers where they were used in many linear, non-linear and
frequency-dependent circuits (summation, integration, …).
• Op-amps are among the most widely used electronic devices today, being used in a vast array of
consumer, industrial, and scientific devices.
• The op-amp is one type of differential amplifier. Op amps can be configured in many different
ways using resistors and other components.
• Most configurations use feedback.
5.1. Introduction
Definition and Notation of Operational Amplifier (Op-Amp)
2

3. Applications of Op Amps
◼ Amplifiers provide gains in voltage or current.
◼ Op amps can convert current to voltage.
◼ Op amps can provide a buffer between two circuits.
◼ Lowpass and bandpass filters.
3
1
4
8 2
3

4. Definition: An operation amplifier OP-AMP is a differential input, DC coupled
amplifier with very large gain.
The signal voltage developed at the output of amplifier is in
phase with the voltage applied to the + input terminal (P-input)
and 180 out of phase with the signal applied to the – input
terminal (N-input).
The vP and vN voltages are therefore referred to as the non-
inverting input and inverting input voltages, respectively.
• vP : non-invert input
• vN : invert input
• v0 : output
• A : open-loop gain
vo = A (vP – vN)
Circuit symbol
4

5. Op Amp Terminals
Terminals of primary interest:
• inverting input
• noninverting input
• output
• positive power supply (+Vcc)
• negative power supply (-Vcc)
Offset null terminals may be used to
compensate for a degradation in
performance because of aging and
imperfections.
The circuit symbol for an op amp
A simplified circuit symbol for an op amp 5

6. Differential and Common-mode Signals
• Rid : the input differential resistance
• R0 : the output resistance
• vid : the differential input voltage:
• vicm : the common-mode input voltage:
6
(+)
(-)
(+)
(-)
id P N
v v v
 −
2
P N
icm
v v
v
+


7. 5.2. Ideal Operational Amplifier (used in circuit analysis)
1. Input voltage difference is zero: vid = 0 → vP = vN
2. Input currents are zero: i+ = i- = 0
Key Characteristics
✓ Infinite voltage gain
✓ Infinite input impedance (does not load the driving sources)
✓ Zero output impedance (drive any load)
✓ Infinite bandwidth (flat magnitude response, zero phase
shift)
✓ Zero input offset voltage.
✓ Infinite Common-mode rejection
✓ The output voltage depends only on the voltage difference
vid and is independent to source and load resistance.
(Why?)
𝑣𝑜 = 𝐴𝑣𝑖𝑑 → 𝐴 =
𝑣𝑜
𝑣𝑖𝑑
A is called the open-loop gain
7
Fig. Equivalent circuit of the ideal op amp.

8. Practical Op-Amp
Real op-amps differ from the ideal model in various respects. In
addition to finite gain, bandwidth, and input impedance, they have
other limitations.
▪ Finite open loop gain.
▪ Finite input impedance.
▪ Non-zero output impedance.
▪ Input current.
▪ Input offset voltage.
▪ Temperature effects
8

9. Terminal Voltages and Currents
Terminal voltage variables Terminal current variables
All voltages are
considered as voltages
rises from the common
node.
All current reference
directions are into the
terminal of the op-amp.
9
We ignore power supply ports

10. 10
Simplified Op-amp Circuit

11. Schematic:
Internal Circuit of 741 Type Op Amp
A component level diagram of the common 741 op-amp. Dotted lines outline: current mirrors
(red); differential amplifier (blue); class A gain stage (magenta); voltage level shifter (green);
output stage (cyan).
11
Differential
Input Load
Stage uses an
Active Load in
the form of a
current mirror

12. The offset null connections
12
The offset null connections (pins 1 & 5) provide a way to balance out the internal variations and zero out
the output offset which might be apparent with zero input voltage. It is used simply by connecting a
trimmer potentiometer between pins 1 & 5. The slider on the potentiometer is connected to the (– V). To
adjust for zero offset, ground the input resistor and use the offset null potentiometer to set the output
voltage precisely to zero. The offset null terminals are not available in packages such as the 5558 & 1458,
which put two independent op amps in a single 8-pin mini-DIP package.

13. Input Signal modes
The input signal can be applied to an op-amp in differential-mode or in
common-mode.
13

14. Signal modes
The input signal can be applied to an op-amp in differential-mode or in
common-mode.
Common-mode signals are applied
to both sides with the same phase on
both.
Usually, common-mode signals are
from unwanted sources, and affect
both inputs in the same way. The
result is that they are essentially
cancelled at the output.
14

15. The graph that relates the output voltage to the input voltage is called the voltage transfer
curve and is fundamental in designing and understanding amplifier circuits.
Transfer Characteristic
Fig.: Voltage transfer characteristic:
( )
( ) ( )
( )
0
CC p n CC
p n CC p n CC
CC p n CC
V A v v V
v A v v V A v v V
V A v v V
− −  −


= − −  −  +


+ −  +


The terminal behavior of the op amp as
linear circuit element is characterized by
constraints on the input voltages and input
currents.
When the magnitude of the input voltage difference (|vp – vn|) is small, the op amp behaves as a linear
device, as the output voltage is a linear function of the input voltages (the output voltage is equal to
the difference in its input voltages times the gain, A.
15

16. 16
Dynamic Response: Negative Feedback Amplifiers
Negative Feedback model of the op-amp circuit:
Going around the loop:
𝑆𝑖𝑑 = 𝑆𝑖𝑛 − 𝑆𝑓; 𝑆𝑜𝑢𝑡 = 𝐴. 𝑆𝑖𝑑; 𝑆𝑓 = 𝐵. 𝑆𝑜𝑢𝑡
Which gives the feedback equation:
1
if 1
1 .
out
in
S A
A
S A B B
= 
+
https://www.wikiwand.com/vi/Harold_Stephen_Black
 Concept was invented on a ferry to Manhattan by
Harold Stephan Black during his morning commute
to Bell Labs in Manhattan in 1927, originally sketched
out on a blank spot of his New York Times
 The idea is bizarre, but really epic
 Completely revolutionized electronics
 9 years before patent office believed it

17. Inverting Configuration (inverting closed-loop configuration)
5.3. Two Configurations for Feedback Circuit Ideal op-amp
Closed-loop gain: G =
𝑣𝑜
𝑣𝐼
= ?
Open-loop gain: A =
𝑣𝑜
𝑣2−𝑣1
→ 𝑣2 − 𝑣1 =
𝑣𝑜
𝐴
= 0 (because 𝐴 → ∞)
Due to 𝑉𝑃 = 0 (grounded) → 𝑉𝑁 = 𝑉𝑃 = 0: The N-point is called the virtual ground
17
1
1
1 1
I I
v v v
i
R R
−
= =
2
1 1 2
1
o I
R
v v i R v
R
= − = −
2
1 1
o
v R
G
v R
= = −
R1
vO
_
+
vI
R2
2
1
3
+
_
𝑉𝑃𝑉2 ; 𝑉𝑁 𝑉1
We can adjust the closed-loop
gain by changing the ratio of R2
and R1

18. (A is finite)
Case of A is finite → 𝑉𝑁 = −
𝑣𝑜
𝐴
(If 𝐴 → ∞ then 𝐺 = Τ
−𝑅2 𝑅1)
non-ideal
gain
18
1
1 1
( / ) /
I o I o
v v A v v A
i
R R
− − +
= =
1 2
o
o
v
v i R
A
= − −
( )
2 1
2 1
/
1 1 / /
o
I
v R R
G
v R R A
−
= =
+ +
5.3. Two Configurations for Feedback Circuit Ideal op-amp
R1
vO
_
+
vI
R2
2
1
3
+
_
Inverting Configuration (inverting closed-loop configuration)

19. ➢ Input Resistance:
➢ Output Resistance:
𝑅𝑜𝑢𝑡 =
𝑣𝑥
𝑖𝑥
𝑣𝑥 = 𝑖2𝑅2 + 𝑖1𝑅1 = 𝑅1 + 𝑅2 𝑖1
𝑖1 = 0 → 𝑣𝑥 = 0
𝑅𝑜𝑢𝑡 = 0
19
5.3. Two Configurations for Feedback Circuit Ideal op-amp
1
1 1
/
I I
i
I
v v
R R
i v R
= = =
Inverting Configuration (inverting closed-loop configuration)

20. Figure: Analysis of the inverting configuration. The circled numbers indicate the
order of the analysis steps.
closed-loop gain
G = -R2/R1
20
5.3. Two Configurations for Feedback Circuit Ideal op-amp
Inverting Configuration (inverting closed-loop configuration)

21. Example 1
21
Consider the inverting configuration with R1 =1 k and R2 =100 k, that is, having an ideal closed-
loop gain of −100.
(a) Find the closed-loop gain for the cases A = 103,104, and 105. In each case determine the
percentage error in the magnitude of G relative to the ideal value of R2/R1 (obtained with A = ∞).
Also determine the voltage v1 that appears at the inverting input terminal when vI = 0.1 V.
(b) If the open-loop gain A changes from 100,000 to 50,000 (i.e., drops by 50%), what is the
corresponding percentage change in the magnitude of the closed-loop gain G?

22. 22
Example 1: Sol.
(a) Substituting the given values in Eq. (*)
( )
2 1
2 1
)
/
1 / /
*
1
(
o
I
v R R
G
v R R A
−
= =
+ +
A |G| 𝝐 vI
103 90.83 −9.17% −9.08 mV
104 99.00 −1.00% −0.99 mV
105 99.90 −0.10% −0.10 mV
𝜖 ≡
𝐺 − Τ
𝑅2 𝑅1
Τ
𝑅2 𝑅1
× 100
Percentage error 𝜖 is defined
The values of vI are obtained from vI = −vO/A = GvI /A with vI = −0.1 V.
(b) Using Eq. (*), we find that for A = 50,000, |G| = 99.80. Thus a −50% change in the open-loop
gain results in a change in |G| from 99.90 to 99.80, which is only −0.1%!

23. Example 2
23
Assuming the op amp to be ideal, derive an expression
for the closed-loop gain vO/vI of the circuit shown in
below Figure. Use this circuit to design an inverting
amplifier with a gain of 100 and an input resistance of
1 M. Assume that for practical reasons it is required
not to use resistors greater than 1 M. Compare your
design with that based on the inverting configuration
of Figure of example 1.

24. 24
Example 2 – Sol.
1 2
1
2
2 2 2
1 1
0
I
I
x I I
v
i i
R
v R
v v i R R v
R R
= =
= − = − = −
2
3
3 1 3
2
4 2 3
1 1 3
0 x
I
I
I
v R
i v
R R R
v R
i i i v
R R R
−
= =
= + = +
0 4 4
0 2 4 4
1 2 3
1
x
I
v v i R
v R R R
v R R R
= −
 
= − + +
 
 

25. Transresistance Amplifier Circuit
Application of an inverting amplifier is that of a "transresistance amplifier" circuit. AKA. a
"transimpedance amplifier", is basically a current-to-voltage converter (Current "in" and
Voltage "out"). They can be used in low-power applications to convert a very small current
generated by a photo-diode or photo-detecting device etc., into a usable output voltage
which is proportional to the input current.
The output voltage is
proportional to the amount of
input current generated by the
photo-diode.
The Inverting Amplifier Circuit – an application
25
5.3. Two Configurations for Feedback Circuit Ideal op-amp

26. Non-inverting Configuration
5.3. Two Configurations for Feedback Circuit Ideal op-amp
(G  closed-loop gain)
𝑉𝑁 = 𝑉𝑃 = 𝑣𝑖
26
0
0
Id
v
v for A
A
= = = 
0 2
1
I
I
v
v v R
R
 
= +  
 
0 2
1
1
I
v R
G
v R
= = +
Feedback
network

27. Non-inverting Configuration
A is finite → 𝑉𝑁 = 𝑣𝐼 −
𝑣𝑜
𝐴
𝑖1 =
𝑣𝑖 − Τ
𝑣𝑜 𝐴
𝑅1
𝑣𝑜 = 𝑣𝑖 −
𝑣𝑜
𝐴
+ 𝑖1𝑅2 = 𝑣𝑖 −
𝑣𝑜
𝐴
+
𝑣𝑖 − Τ
𝑣𝑜 𝐴
𝑅1
𝑅2
27
5.3. Two Configurations for Feedback Circuit Ideal op-amp
( )
( )
2 1
2 1
1 /
1 / 1
1
O
I
R R
v A
G
R R
v A
A

+
 = =
+ +
+
1
1 2
feedback factor
loop gain
where is know as the
A is the
R
R R


=
+
If A >> 1 → G  1/ = 1 +
𝑅2
𝑅1
approaches the infinite gain result
Real op-amp do not have “infinite” “open loop (without feedback)”
gain A.

28. Non-inverting Configuration
28
5.3. Two Configurations for Feedback Circuit Ideal op-amp
Input & Output resistances of the non-inverting
amplifier
Using the assumption:
𝑅𝑖𝑛 =
𝑣𝑆
𝑖𝑁
= ∞ because iP = 0
To find the output resistance, a test current (ix) source is applied to
the output terminal and the source vS is set to 0.
The output of the non-inverting amplifier is taken at the terminals
of the ideal voltage source A(vP – vN), thus the output resistance of
the non-inverting configuration is zero.
Rout = 0
ix
+
_
+
_
R2
R1 i1
i2
i_
ix

29. Non-inverting Configuration
Voltage follower
What happens if
𝑹𝟏 = ∞ and 𝑹𝟐 = 𝟎?
29
5.3. Two Configurations for Feedback Circuit Ideal op-amp
( )
( )
2 1
2 1
1 /
1 /
1
O
I
R R
v
G
R R
v
A
+
 =
+
+
Consider the effect of the finite op-amp
open-loop gain A on the gain of the
noninverting configuration.
+
_
v0
vs
P
N
vid +
In the special case of R1 = , R2 = 0:
The follower amplifier with G  1
But Rin is very high
Rout is very low
➔Using it as a buffer for matching
impedances.

30. Summing Amplifier (weighted summer )
6.4. Some Application Circuits
A weighted summer
 weighted summer - is a closed-loop
amplifier configuration which provides an
output voltage which is weighted sum of the
inputs.
30
1 2
1 2
1 2
, , ..., n
n
n
v
v v
i i i
R R R
= = = 1 2 ... n
i i i i
= + + +
0
O f f
v iR iR
= − = − 1 2
1 2
...
f f f
O n
n
R R R
v v v v
R R R
 
= − + + +
 
 
If R1 = R2 = ….= Rn  R then ( )
0 1 2 ...
f
n
R
v v v v
R
= − + + +

31. Summing Amplifier
A weighted summer capable of implementing summing coefficients of both
signs (summing signals with opposite signs).
31
6.4. Some Application Circuits
1 2 3 4
1 2 3 4
a c a c c c
O
b b
R R R R R R
v v v v v
R R R R R R
     
     
= + − −
     
     
     
     

32. 32
Summing Amplifier:
6.4. Some Application Circuits
Example:
Use inverting amplifiers to design a circuit that performs the operation
υo = 4υ1 + 7υ2

33. 33
Summing Amplifier:
6.4. Some Application Circuits
Example: To performs the operation υo = 4υ1 + 7υ2
Solution:
+
-
R1
Rf1
vo1
v1 R2
v2
+
-
Rs2
Rf2
vo2
Stage 1: Inverting
summing amp.
Stage 2: Inverting amp.
The desired circuit has to amplify υ1 by a factor of
4, amplify υ2 by a factor of 7, and add the two
together.
@ 1st stage, we need to select values for R1, R2,
and Rf1
𝑅𝑓1
𝑅1
= 4 𝑎𝑛𝑑
𝑅𝑓1
𝑅2
= 7
Randomly, choose Rf1 = 56 k, → specifies the
other resistors:
R1 = 14 k and R2 = 8 k.
@ 2nd stage, a gain of (−1) requires that
𝑅𝑓2
𝑅𝑠2
= 1 You can select any resistor’s values, freely, ex. Rf2 = Rs2 = 10 k
1
1 1 2
1 1
2
f
o
f
v
R
v
R
R R
v
   
= − + −
   
   
1
2
2
2
o o
f
s
v
R
R
v
 
= −
 
 

34. Summing Amplifier Applications
Summing Amplifier Audio Mixer
If the input resistances of a summing amplifier are connected to potentiometers the
individual input signals can be mixed together by varying amounts. For example,
measuring temperature, you could add a negative offset voltage to make the display
read "0" at the freezing point or produce an audio mixer for adding or mixing together
individual waveforms (sounds) from different source channels (vocals, instruments, etc)
before sending them combined to an audio amplifier.
34

35. Summing Amplifier Applications
Digital to Analogue Converter (DAC summing amplifier circuit)
Another useful application of a Summing Amplifier is as a weighted sum digital-to-
analogue converter. If the input resistors, Rin of the summing amplifier double in value for
each input, for example, 1kΩ, 2kΩ, 4kΩ, 8kΩ, 16kΩ, etc., then a digital logical voltage,
either a logic level "0" or a logic level "1" on these inputs will produce an output which is the
weighted sum of the digital inputs. Consider the circuit below.
35

36. Difference Amplifiers
❑difference amplifier – is a closed-loop configuration which responds
to the difference between two signals applied at its input and ideally
rejects signals that are common to the two.
➢ Ideally, the amp will amplify only the differential signal (vId) and
reject completely the common-mode input signal (vIcm). However,
a practical circuit will behave as below…
differential gain
differential input
common-mode input
common-mode gain
36
m
Id
Out d cm Ic
v A
v
A v
= +

37. 37
Difference Amplifiers
▪ Common-mode rejection ratio (CMRR)
is the degree to which a differential
amplifier “rejects” the common-mode
input.
Fig.: Representing the input signals to a
differential amplifier in terms of their
differential & common-mode
components.
20log
cm
d
C RR
A
A
M = Ideally, CMRR = infinity…
❑ Ideal difference amplifier:
✓ Responds to differential input signal vId
✓ Rejects the common-mode input signal vIcm
❑ Practical difference amplifier:
▪ vO = AdvId + AcmvIcm
✓ Ad is the differential gain
✓ Acm is the common-mode gain
vIcm
vId
vId
vI2 = vIcm + vId/2
vI1 = vIcm – vId/2
vId = vI2 – vI1
1
2
1
2
vIcm = (vI1 + vI2)
1
2

38. 38
(A Single Op-Amp) Difference Amplifier (Substractors)
(Mixed Configuration)
( )
2
0 1 2
1
R
v v v
R
= −
3
1
2 4
R
R
R R
=
If set then
( )
( )
4 1 2 2
1 2
1 3 4 1
o
R R R R
v v v
R R R R
+
= −
+
2
1 2
0
n n o
n
v v v v
i
R R
− −
+ + =
4
1
4 3
n p
R
v v v
R R
= =
+
Apply the KCL @ the inverting input node (vn):
Op amp is ideal: in = ip = 0 , and
+
-
R1
R2
v1
vo
v2
R3
R4
RL
i
i
vn
vp
+
-
in
ip
Simplified difference-amplifier equation
subtracts!
Combining the 2 configurations
① Differential input signal
Assume an ideal op amp operating in its linear region.
This circuit amplify only differences! If a common signal is applied to both the inputs, it will be rejected!

39. 39
(A Single Op-Amp) Difference Amplifiers
Another way of solving: use superposition
Assume the circuit is linear
① Differential input signal
𝒗𝟐 = 𝟎
Inverting amplifier
𝒗𝟏 = 𝟎 Non inverting amplifier
2
2 2
1
O
R
v v
R
= −
+
-
R1
R2
vo2
v2
R1 R2
RL
i
i
+
-
+
-
R1
R2
v1
vo1
R1
R2
RL
vp
+
-
1 2
1
1
1 2 1 2
1 2 1
2
1
1
.
o p
R R
v v
R
v R R R
R R R
R
v
R
+
=
+
=
+
=
( )
2
1 2 1 2
1
o o o
R
v v v v v
R
= + = − Still subtracts!
Since the net output voltage is the sum of the individual terms

40. ② Common – mode input signal
(note: 𝑖2 = 𝑖1)
𝑣𝑜 = 0 → 𝐴𝑐𝑚 = 0 However, any mismatch in the resistance
ratios can make 𝑨𝒄𝒎 nonzero, and hence
CMRR is finite.
40
4
1
1 4 3
1
Icm Icm
R
i v v
R R R
 
= −
 
+
 
4
0 2 2
4 3
Icm
R
v v i R
R R
= −
+
3
4 2
0
4 3 1 4
1
Icm
R
R R
v v
R R R R
 
= −
 
+  
4 2
3 1
R R
R R
=
Let
(A Single Op-Amp) Difference Amplifiers

41. Differential Input Resistance 𝑅𝑖𝑑
41
1
1 1 1 1 1 1
1
0 2
2
id
id
id
id
v
R
i
v i R i R i R
R R
=
= + + =
=
(A Single Op-Amp) Difference Amplifiers
② Common – mode input signal
If the amplifier is required to have a large gain then R1 will relatively small and
consequently the input resistance will be correspondingly small ➔ Drawback!
How can we solve this Drawback?
We can use buffers (voltage followers)

42. Instrumentation Amplifier
Due to the input resistance of the difference amplifier is too low, the instrumentation
amplifier should be used. It is a combination between 2 non-invert amplifiers and a difference
amplifier so that this scheme becomes a high-qualified amplifier.
Stage 1:
𝑣𝑜1 = (1 +
𝑅2
𝑅1
)𝑣𝐼1
𝑣𝑜2 = (1 +
𝑅2
𝑅1
)𝑣𝐼2
stage #1 stage #2
42
(Khuếch đại đo lường / khuếch đại đo đạc )
2
1
1
1 I
R
v
R
 
= +
 
 
2
2
1
1 I
R
v
R
 
= +
 
 
+
-
R2
A1
R1
R3
A2
R2
+
-
-
vo2
vo1
X
R4
A3
-
R4
+
R1
vo
R3
+
vI1
vI2

43. +
-
R2
A1
R1
R3
A2
R2
+
-
-
vo2
vo1
X
R4
A3
-
R4
+
R1
vo
R3
+
vI1
vI2
Stage 2:
𝑣𝐼1
′
= (1 +
𝑅2
𝑅1
)𝑣𝐼1
𝑣𝐼2
′
= (1 +
𝑅2
𝑅1
)𝑣𝐼2
𝑣𝑖𝑑
′
= 𝑣𝐼2
′
− 𝑣𝐼1
′
𝑣𝐼1
′
𝑣𝐼2
′
𝑣𝑖𝑑
′
= 1 +
𝑅2
𝑅1
𝑣𝐼2 − 𝑣𝐼1
𝑣𝑖𝑑
′
= 1 +
𝑅2
𝑅1
𝑣𝑖𝑑
𝑣𝑜 =
𝑅4
𝑅3
𝑣𝑖𝑑
′
Instrumentation Amplifier
43
4 2
0
3 1
1 Id
R R
v v
R R
 
= +
 
 
4 2
3 1
1
d
R R
A
R R
 
= +
 
 
0
cm
A =
2
2
1
1 I
R
v
R
 
= +
 
 
2
1
1
1 I
R
v
R
 
= +
 
 

44. Advantages:
✓ Very high (ideally infinite) input resistance; High differential gain
✓ Very low DC offset, low drift, low noise, very high CMRR.
Disadvantages:
✓ 𝒗𝑰𝒄𝒎 is amplified in Stage 1 by a gain equal to that experienced by 𝑣𝐼𝑑. This is a very
serious issue, for it could result in the signals at the outputs of A1 and A2 being of such
large magnitudes that the op amps saturate. But even if the op amps do not saturate, the
difference amplifier of Stage 2 will now have to deal with much larger common-mode
signals, with the result that the CMRR of the overall amplifier will inevitably be reduced.
✓ The two amplifier channels in Stage 1 have to be perfectly matched, otherwise a spurious
signal may appear between their two outputs. Such a signal would get amplified by the
difference amplifier in the Stage 2.
✓ To vary the differential gain 𝐴𝑑, two resistors 𝑅1 have to be varied simultaneously. At each
gain setting the two resistors have to be perfectly matched: a difficult task.
Instrumentation Amplifier
44

45. 0
+
- R2
A1
2R1
R3
A2
R2
+
-
-
vo2
vo1
R4
A3
-
R4
+
R3
+
vI1
vI2
0
+
_
0V
0V
+
_
+
_
vI2 – vI1 = vId
vId /2R1
vId /2R1
vId /2R1
Instrumentation Amplifier
45
2
2 1
1
2
1
2
O O Id
R
v v v
R
 
− = +
 
 
( )
4 4 2
2 1
3 3 1
1
o O O Id
R R R
v v v v
R R R
 
= − = +
 
 
4 2
3 1
1
d
R R
A
R R
 
= +
 
 
This circuit is often called Instrumentation Amplifier.
4 2
3 1
1 I
o d
R
v
R R
R
v
 
= +
 
 
1
2
2
1
2
Id
v
R
R
 
+
 
 
+
_ With this circuit, we
can adjust the gain,
just changing R1

46. Example 3
Design the instrumentation amplifier circuit in the above to provide a
gain that can be varied over the range of 2 to 1000 utilizing a 100 k
variable resistance (a potentiometer, or “pot” for short).
46

47. 47
4 2
3 1
1
d
R R
A
R R
 
= +
 
 
2
1 1
2
1
2
1
2
1 2...1000
2
1 1000
2
1 2
100
f v
f
f
R
R R
R
R
R
R k
+ =
+

+ =



 + =
 + 


48. Integrators and Differentiators
Fig.: The inverting configuration with general impedances
Closed-loop transfer function
48
2
1
( ) ( )
( ) ( )
N
O
I
UT
V s Z
Z
V
s
s s
= −
(in s-domain or frequency domain)
❖ By placing different circuit elements into Z1 & Z2, we can get interesting
operations. Some examples…
✓ Integrator
✓ Differentiator
✓ Summer
✓ Unity–Gain Buffer
+
+
-
Z1 Z2
VOUT
VIN
_
+
_

49. Integrators
Miller or Inverting Integrator
𝑖1(𝑡) flows through the capacitor C, causing
charge to accumulate on C equal to‫׬‬
0
𝑡
𝑖1(𝑡) 𝑑𝑡.
Capacitor voltage 𝑣𝑐(𝑡) charges by
1
𝐶
‫׬‬
0
𝑡
𝑖1 𝑡 𝑑𝑡.
initial voltage on C
Output voltage
49
1
0
1
( ) ( )
t
C C
v t V i t dt
C
= + 
0
1
( ) ( )
t
O I C
v t v t dt V
CR
= − −

( ) ( )
O C
v t v t
= −
1
( )
( ) I
v t
i t
R
=
in the time domain

50. Integrators
For physical frequencies, 𝑠 = 𝑗𝜔
And phase:
Integrator frequency:
Frequency response
Magnitude of integrator transfer function:
50
1 2
1
( ) & ( )
Z s R Z s
sC
= =
(in s-domain or frequency domain)
2
1
1
( ) ( ) 1
( ) ( )
o
i
V s Z s sC
V s Z s R sCR
= − = − = −
( ) 1
( )
o
i
V j
V j j CR

 
= −
1
o
i
V
V CR

= 90
 = + 
int
1
CR
 =
Fig. The square wave (upper waveform) applied to the input of
the integrator produces the triangle wave at the integrator
output (lower waveform)
ω = 0→ dc problem!

51. Integrators
Miller or Inverting Integrator with 𝑹𝑭
𝑖1 =
𝑣𝐼
𝑅
𝑍 = 𝑅𝐹 ∥
1
𝑠𝐶
=
𝑅𝐹
1 + 𝑅𝐹𝑠𝐶
𝑣𝑜 = 0 − 𝑖1𝑍 = −
Τ
𝑅𝐹 𝑅
1+𝑠𝑅𝐹𝐶
𝑣𝑖
51
0 ( ) /
( ) 1
F
i F
V s R R
V s sCR
= −
+
(in s-domain)
Fig.: A feedback resistor RF
lowers the DC gain of the
integrator, creating a more
practical integrator circuit.
Fig.: The practical integrator circuit has a frequency response that starts
out flat at DC and then rolls off with frequency.
Example: a plot of the circuit gain versus
frequency, with R = RF = 1kΩ and C = 1μF.
These component values produce a single-
pole response with the -3 dB frequency of
1/(2πRFC) = 160 Hz.
The dc problem of the integrator circuit can be
alleviated by connecting a resistor RF

52. Example 4
Find the output produced by a Miller integrator in response to an input
pulse of 1-V height and 1-ms width [below figure]. Let R=10 k and
C = 10nF. The op amp is specified to saturate at ±13𝑉.
52

53. Differentiator
𝑖(𝑡) = 𝐶
𝑑𝑣𝐼(𝑡)
𝑑𝑡
𝑣𝑜(𝑡) = 0 − 𝑖(𝑡)𝑅
→ 𝑣𝑜(𝑡) = −𝑅𝐶
𝑑𝑣𝐼(𝑡)
𝑑𝑡
𝑧1 𝑠 =
1
𝑠𝐶
𝑎𝑛𝑑 𝑧2 𝑠 = 𝑅
𝑉
𝑜(𝑠)
𝑉𝑖(𝑠)
=
𝑧2(𝑠)
𝑧1(𝑠)
= −𝑠𝐶𝑅
The transfer function (in s-domain):
Frequency response
with a time-constant CR
53
0 ( )
( )
i
V j
j CR
V j



= −
0
90
i
V
CR
V


=
= − 

54. DC Imperfections
Offset voltage
54

55. Exercise
Use the model as shown in Figure to sketch the
transfer characteristic 𝑣𝑜versus 𝑣𝐼𝑑 (𝑣𝑜 ≡ 𝑣3
and 𝑣𝐼𝑑 ≡ 𝑣2 − 𝑣1) of an op amp having an
open-loop dc gain 𝐴𝑜 = 104 V/V, output
saturation levels of ±10 𝑉 and 𝑣𝑜𝑠 of +5 mV.
55

56. 56
Figure: Transfer characteristic of an op amp
with VOS = 5 mV.
Exercise – Sol.

57. DC Imperfections
Offset voltage
Output DC voltage can have a large magnitude
The output dc offset voltage of an op
amp can be reduced to zero by
connecting a potentiometer to the
two offset-nulling terminals.
57
2
0
1
1
OS
R
V V
R
 
= +
 
 

58. DC Imperfections
Offset voltage
One way to overcome the dc offset problem is by capacitively coupling the amplifier.
(b) Equivalent circuit for determining
its DC output offset voltage 𝑉
𝑜
(a) Capacitively coupled inverting amplifier
✓ Not required to amplify DC or very-low frequency signal
58

59. DC Imperfections
Input Bias and Offset Currents
✓ Offset Currents
✓ Input bias current
𝐼𝐵 = 100 𝑛𝐴 𝑎𝑛𝑑 𝐼𝑜𝑠 = 10 𝑛𝐴
59
1 2
2
B B
B
I I
I
+
=
1 2
OS B B
I I I
= −

60. DC Imperfections
Input Bias and Offset Currents
Reducing the effect of the input bias currents by introducing R3
In case 𝐼𝐵1 = 𝐼𝐵2 = 𝐼𝐵
If then 𝑉
𝑜 = 0
The effect of the input bias currents is removed
Denote
Minimize the effect of the
input bias currents
60
1 2 2
o B B
V I R I R
= 
2 3 2 1 2 3 1
( / )
o B B B
V I R R I I R R
= − + −
2
2 3
1
1
o B
R
V I R R
R
 
 
= − +
 
 
 
 
1 2
3
1 2
R R
R
R R
=
+
1
2
/ 2
/ 2
B B OS
B B OS
I I I
I I I
= +
= −
0 2
OS
V I R
=

61. DC Imperfections
Input Bias and Offset Currents
RC-coupled amplifier
61

62. Effect of 𝑽𝒐𝒔 and 𝑰𝒐𝒔 on the operation of the inverting integrator
-
+
R
C
OS
V
OS
V
OS /
V R
OS /
V R
+
-
o
v
OS
OS
0
OS
OS
1
t
o
V
v V dt
C R
V
V t
CR
= +
= +

Effect of 𝑽𝒐𝒔
Effect of 𝑰𝒐𝒔
62

63. Frequency Dependence of the Open-Loop Gain
Where: s = jω
Ao: Open loop gain at DC
ωB: Open loop BW
ωT: unity-gain freq. (where |AOpenLoop(s)| = 1)
( )
1 /
(j )
1 /
o
OpenLoop
B
o
OpenLoop
B
A
A s
s
A
A
j


 
=
+
=
+
(j ) o B
o B
A
A
A



 
=
=
63
To this point we have assumed the open loop gain, AOpenLoop,
of the op amp is constant at all frequencies.
Real Op amps have a frequency dependent open loop gain.
Amplifiers have finite gain and BW. Here’s an example of
the open-loop gain vs. frequency plot of an amplifier.
Notice that the gain can be very high at low frequency, but
starts to roll off at a low frequency also. They are also
“frequency compensated” to roll off at -20dB/dec (or a single
pole) to guarantee that op amp circuits will be stable.
We can represent frequency response characteristics of
this amplifier as
If ω >> ωB,

64. 64
Frequency Dependence of the Open-Loop Gain
Real Op Amp Frequency Response
( ) 2 2 2
2
1
O B O
OpenLoop
B
B
A A
A j


  

= =
+
+
At Low Frequencies: OpenLoop O
A A
=
At High Frequencies:
O B T
OpenLoop
A
A
 
 
=
For most frequencies of interest, ω>>ωB , the product of
the gain and frequency is a constant, ωT
Gain - Bandwidth Product ( )
2
T
T
f GBW


= 
If the open loop bandwidth is so small, how can the op amp be useful?
The answer to this is found by considering the closed loop gain.

65. Frequency Dependence of the Closed-Loop Gain
65
Therefore, the closed-loop gain has a response that rolls off at –20 dB/dec at a
frequency, ω3dB, that is a function of the gain set by the input and feedback resistors.
1
O
I
v A
G
v A

 =
+
Previously, in slide #29 we found that the closed loop gain for the Noninverting configuration was
(for finite open loop gain):
1
1 2
R
R R
 =
+
Using the frequency dependent open loop gain:
( )
( )
( )
( )
@
1 1
1 1 1
1
1
O
o B
O
B
O o B
DC
I B O
o B
B O H
B
A
A
A
s
V A
A
G s G
s s
V A s A
A
A
s


 
  


  

   
   
+
+
   
 = = = = =
+ + +
   
+
+  
  +
+  
 
Where, H  Upper cutoff frequency (closed loop bandwidth) = B(1 + AO)
Low Pass

66. 66
Frequency Dependence of the Open-Loop Gain
Real Op Amp Frequency Response
The closed Loop
Amplifier has a lower
gain than the Open
Loop Amplifier
The closed Loop Amplifier has a higher
bandwidth than the Open Loop Amplifier
Closed loop bandwidth:
H = B(1 + AO) =
@
T
DC
G

Closed loop DC gain:
1
A
G
A

=
+

67. 67
Frequency Dependence of the Open-Loop Gain
Real Op Amp Frequency Response
( ) ( )
OpenLoop CloseLoop
Gain Bandwidth Gain Bandwidth
 = 

68. Example 5
Consider an op amp with ft = 1 MHz. Find the 3-dB frequency of closed-loop
amplifiers with nominal gains of +1000, +100, +10, +1, −1, −10, −100, and −1000.
Sketch the magnitude frequency response for the amplifiers with closed-loop gains
of +10 and –10.
68
3dB
2 1
1 /
t
R R

 =
+
Sol.:

69. Frequency response of an
amplifier with a nominal
gain of +10 V/V.
Frequency response of an
amplifier with a nominal
gain of −10 V/V.
69

70. Large-Signal Operation of Op Amps
-
+
0
t
0
t
15V
13V
-15V
-13V
1 1
R k
= 
2 9
R k
= 
P
V
I
v
0
i
L
i
F
i
L
R
0
v
0
v
❑ Output Voltage Saturation
❑ Output Current Limits
70

71. Example 6
Consider the noninverting amplifier circuit shown in the
figure. The circuit is designed for a nominal gain
(1+ ൗ
𝑅2 𝑅1) =
10𝑉
𝑉
. It is fed with a low-frequency sine-wave
signal of peak voltage 𝑉𝑃 and is connected to a load resistor
𝑅𝐿. The op amp is specified to have output saturation
voltages of ±13 𝑉 and output current limits of ±20 𝑚𝐴.
(a) For 𝑉𝑃 = 1 V and 𝑅𝐿 = 1 k, specify the signal
resulting at the output of the amplifier.
(b) For 𝑉𝑃 = 1.5 V and 𝑅𝐿 = 1 k, specify the signal
resulting at the output of the amplifier.
(c) For 𝑅𝐿 = 1 k, what is the maximum value of 𝑉𝑃 for
which an undistorted sinewave output is obtained?
(d) For 𝑉𝑃 = 1 V, what is the lowest value of 𝑅𝐿 for
which an undistorted sinewave output is obtained?
71

72. 72
In fact, the output does not look like a copy of the input!
❖The input signal cannot be too big: OUTPUT VOLTAGE SATURATION
❖The input signal cannot change too fast: SLEW RATE
❖The input signal certainly cannot be too be and change too fast: FULL
POWER BANDWIDTH
Linear Amplifier
“Real” amplifiers are linear!
If the input signal becomes too large, and/or the input signal changes too quickly,
➔ some very non-linear behavior

73. Slew rate
max
( )
/
o
dv
SR
t
V
d
s

=
Maximum rate of change (slew
rate  SR) possible @ the
output of a real op amp
73
Unity-gain follower circuit
Linearly rising output waveform
obtained when the amplifier is slew-
rate limited.
Exponentially rising output waveform obtained when V is
sufficiently small so that the initial slope (ωtV) is smaller than
or equal to SR
Input step waveform

74. Full-Power Bandwidth
Max: 𝜔 ෠
𝑉𝑖
What happens if 𝜔 ෠
𝑉𝑖 exceeds SR?
𝑓𝑀: full-power bandwidth
𝑉
𝑜𝑚𝑎𝑥: Rated output voltage
74
ˆ cos
I
i
dv
V t
dt
 
=
max
max
2
M o
M
o
V SR
SR
f
V


=
=
ˆ sin
I I
v V t

=

75. Effect of slew-rate limiting on output sinusoidal waveforms
75
Full-Power Bandwidth

76. Some Nonlinear Electronic Circuits used OP-AMP
76
Anti-logarithmic Amplifier
2 exp
O S
T
in
v
v
I R
V
 
= −  
 
+
-
R2
R
vo
vin
vN
vP
IF
I
+
-
Logarithmic Amplifier
( ) ( )
1 1
1
1
exp exp
ln ln ln
N N O O
S S
T T
O T
in in
in
i
T T
n S
S
v v v v
I I
R V R V
v V
v
I
v
v
v
V V I R
R
   
− − −
=  =
   
   
= − = − +
( )
ln
O in
v a v b
= − +
+
-
R1
R
vo
vin
vN
vP
IR
+
-

77. Analog Signal Comparator
Comparator indicates when a given signal exceeds a predetermined value. The simplest form
of comparator is a high-gain differential amplifier made with an op-amp. The op-amp goes
into positive or negative saturation according to the difference of the input voltages.
This simple comparator has the disadvantage. For a
very slowly varying input, the output swing can be
rather slow. If the input is noisy, the output may make
several transitions as the input passes through the
trigger point. This problem can be resolved by the use
of positive feedback called Schmitt-trigger.
77

78. Schmitt-trigger
Complete voltage transfer characteristic
for the Schmitt trigger.
The 1st threshold
78
When Vo = +VCC then: 1
1 2
REF CC
R
V V
R R
=
+
The 2nd threshold
When Vs = -VEE then Vo  VCC,
1
1 2
REF EE
R
V V
R R
= −
+
1
1 2
CC
R
V
R R
+
if Vin  to
then switching occurs and Vo becomes -VEE.
and VREF changes to 1
1 2
EE
R
V
R R
−
+
When Vo = -VEE then:
The opposite happens as Vs decreases from VCC.
1
1 2
EE
R
V
R R
−
+
1
1 2
CC
R
V
R R
+
1st
threshold
vo
vs
-VEE
0
VCC
2nd
threshold
+
-
R1 R2
vs
VCC
-VEE
vo
VREF

79. 79
Typical Comparator Circuit
E.g.
LM119
Dual
comparator

80. 80
Other good references…
• Texas Instruments Comprehensive Op-Amp Application Note
https://web.mit.edu/6.101/www/reference/op_amps_everyone.pdf
• MIT Pole/Zero Tutorial
https://web.mit.edu/2.14/www/Handouts/PoleZero.pdf
https://ocw.mit.edu/ans7870/RES/RES.6-010/MITRES_6-010S13_comchaptrs.pdf
• OPERATIONAL AMPLIFIERS: Theory and Practice