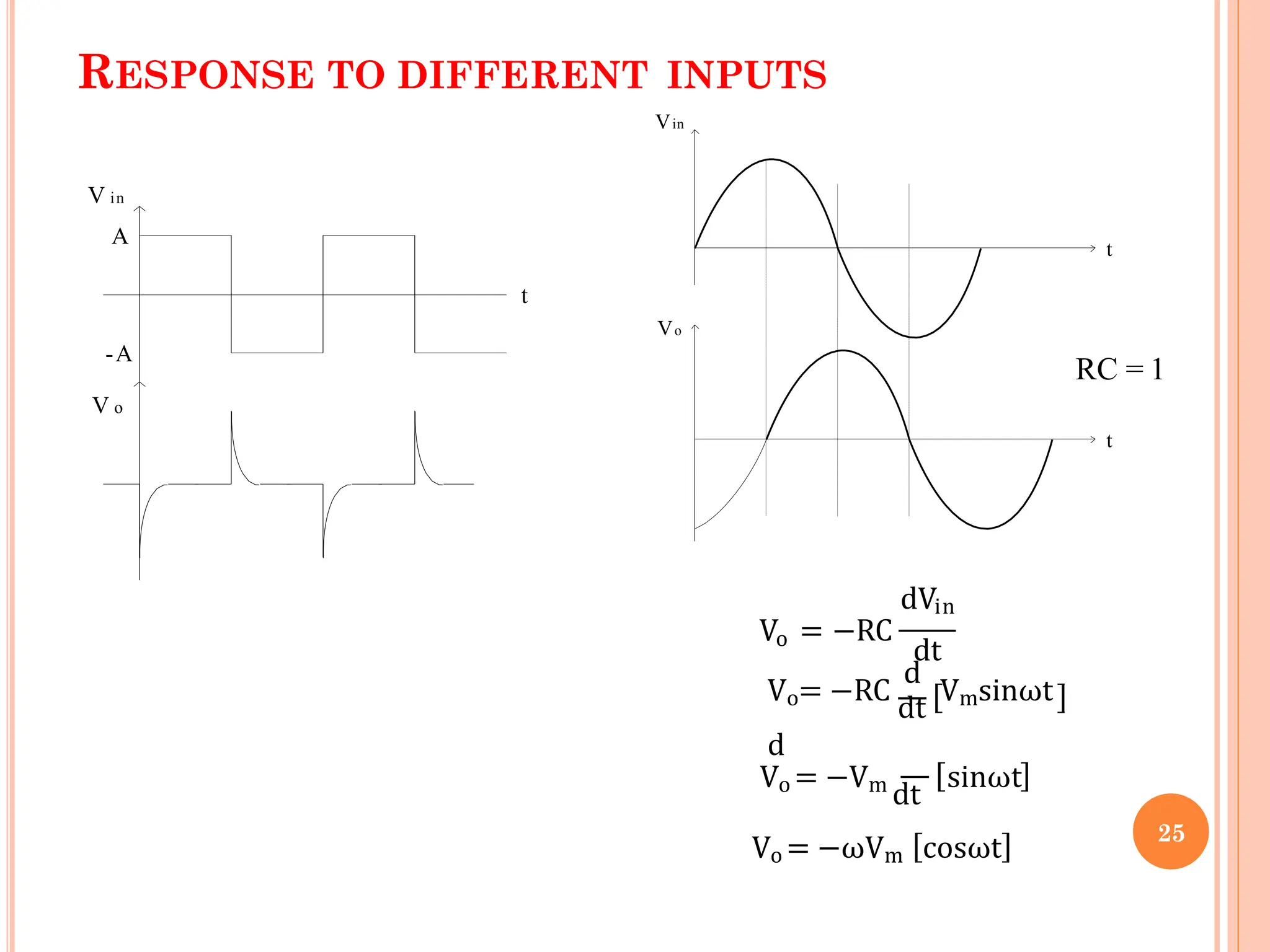
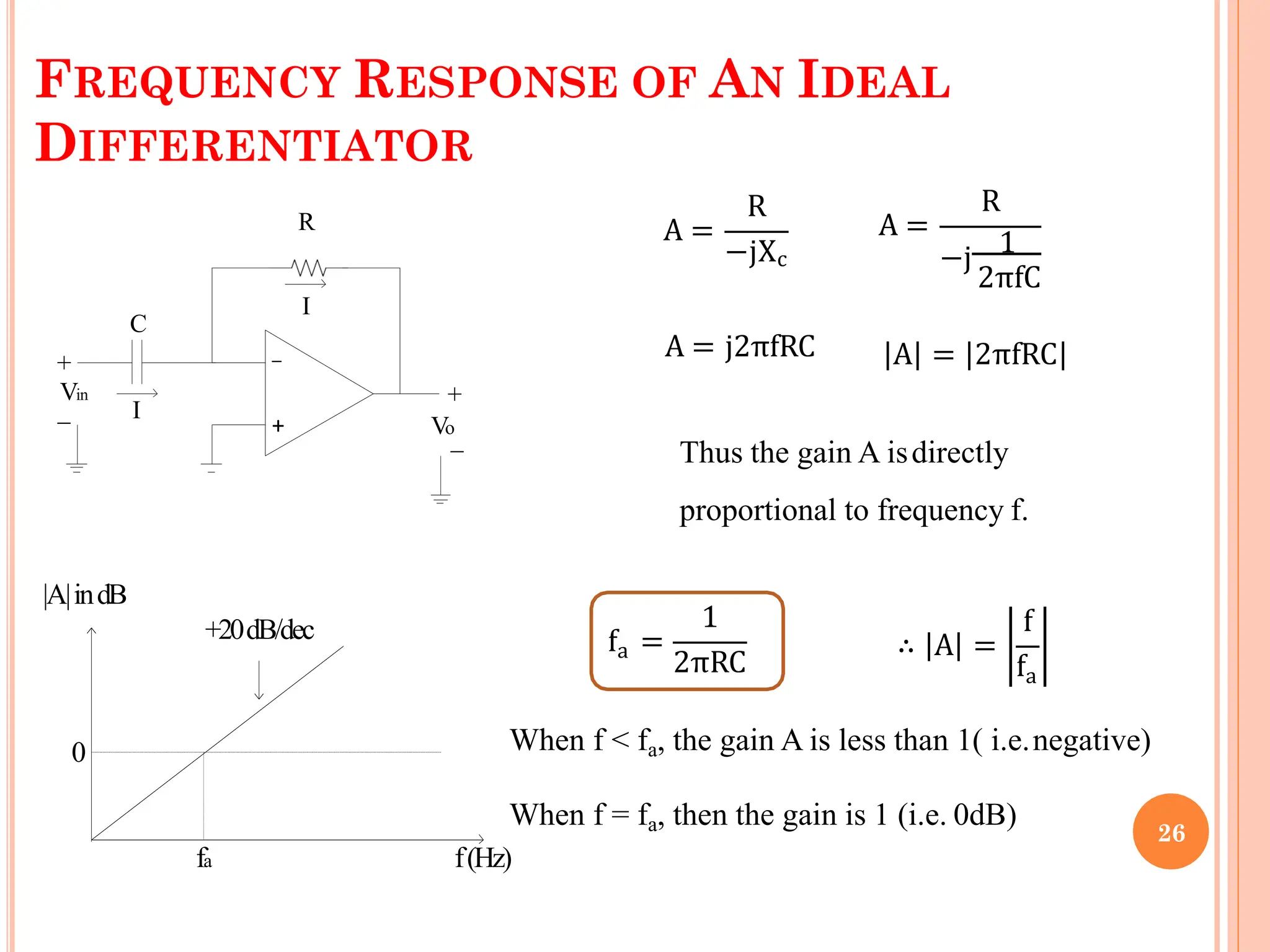
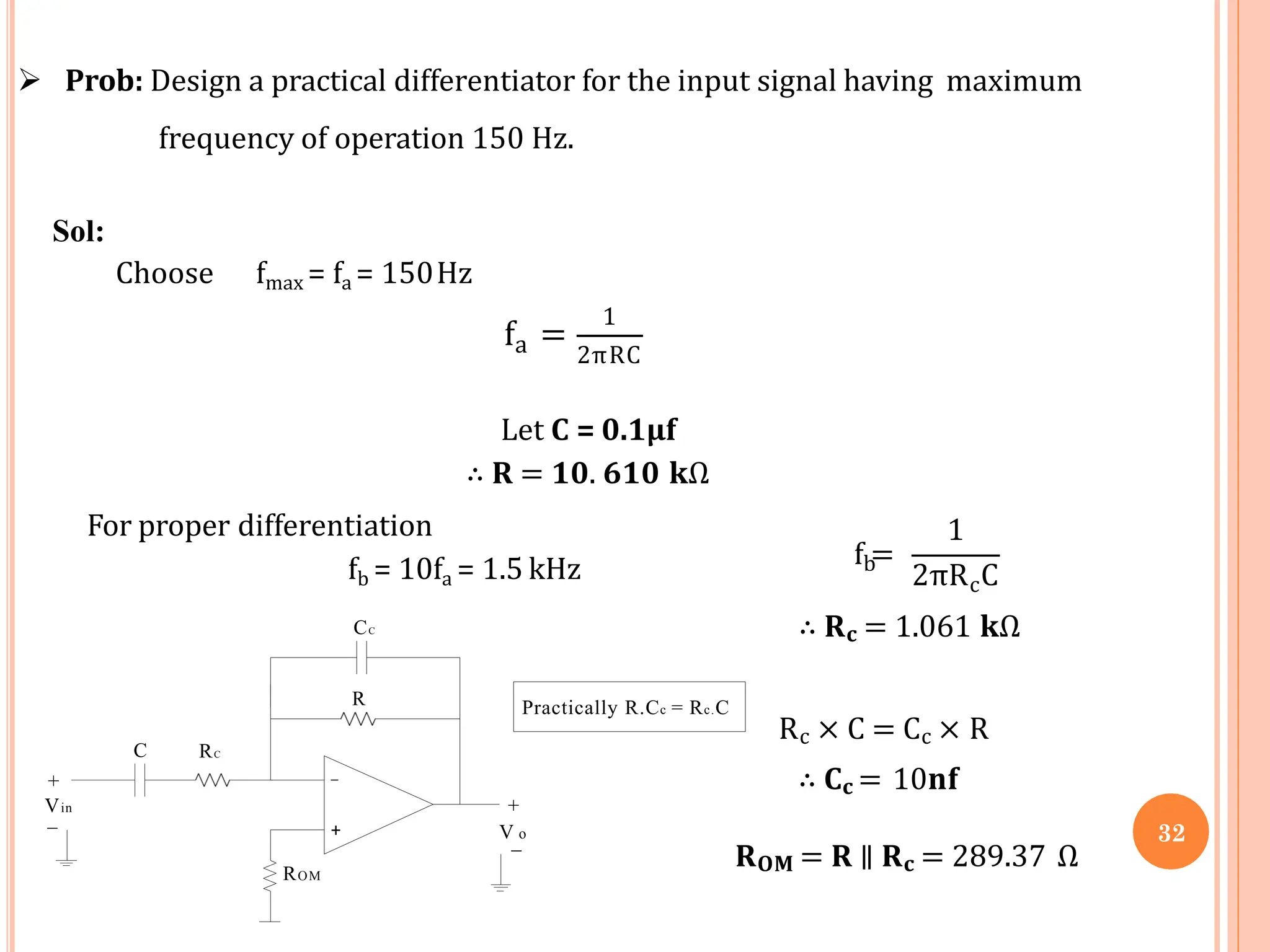
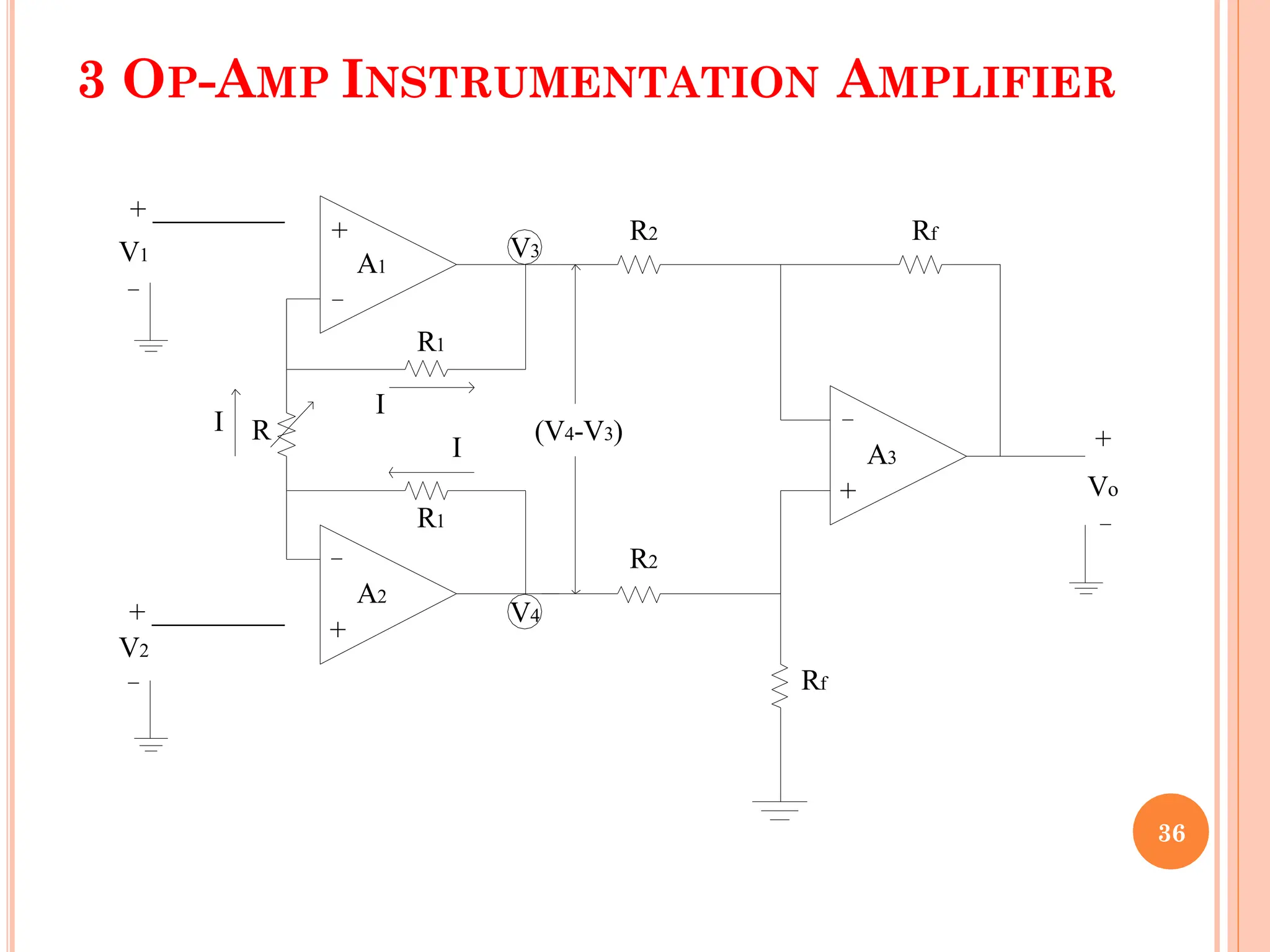
This document contains a presentation on op-amp applications, covering various amplifier types and their functionalities including inverting/non-inverting amplifiers, summing and differential amplifiers, and integrators/differentiators. It also highlights the characteristics and design considerations for practical versions of these circuits, including instrumentation amplifiers and their applications. The content is supported by detailed circuit diagrams and frequency response analysis for different op-amp configurations.
![A
Presentation
on
Op-Amp Applications
[UNIT-V]
1](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-1-2048.jpg)



![LECTURE # 02
Summing Amplifier [2 Input]
Inverting & Noninverting Type
Difference Amplifier [ Subtractor]
10](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-10-2048.jpg)


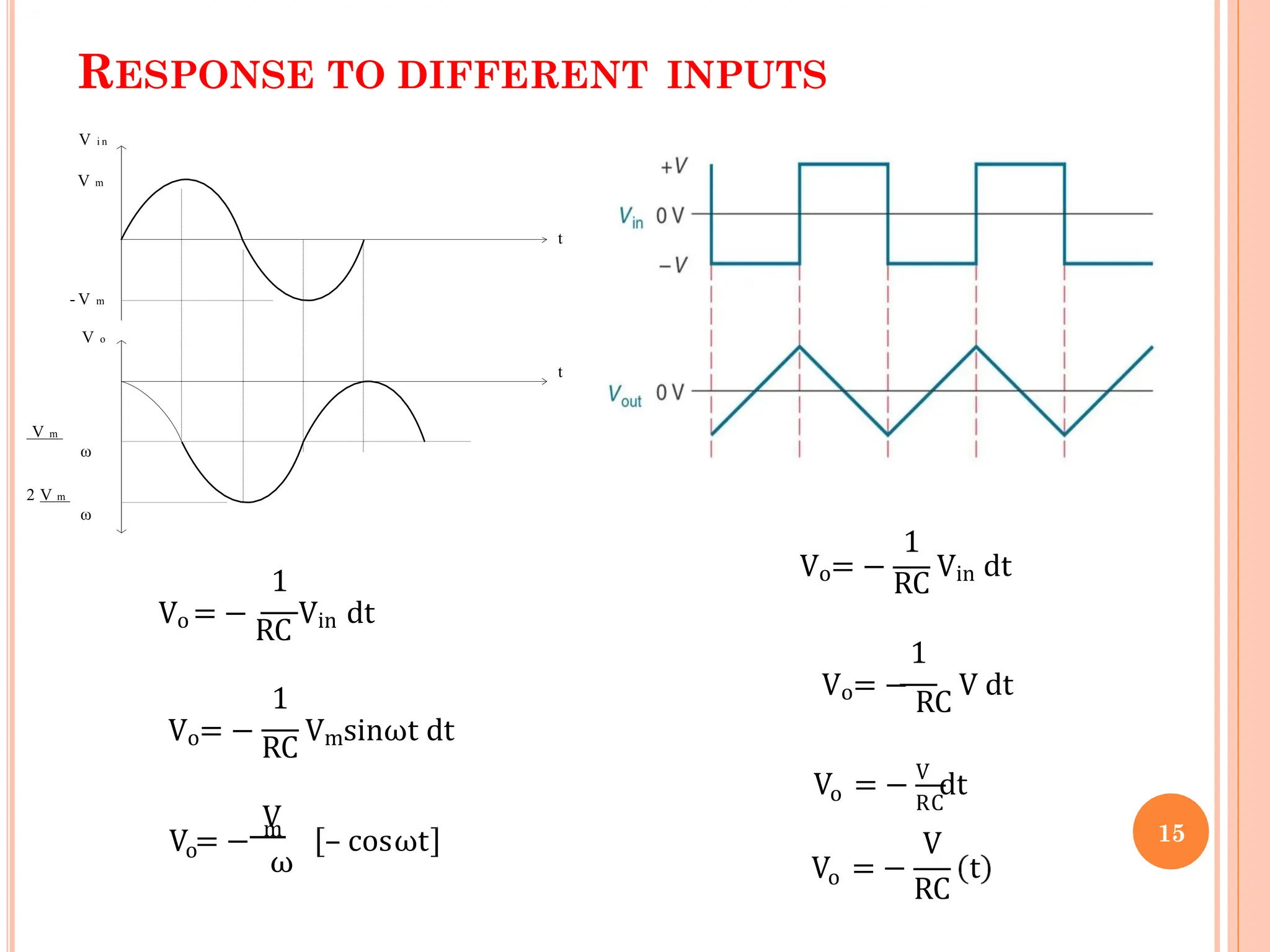
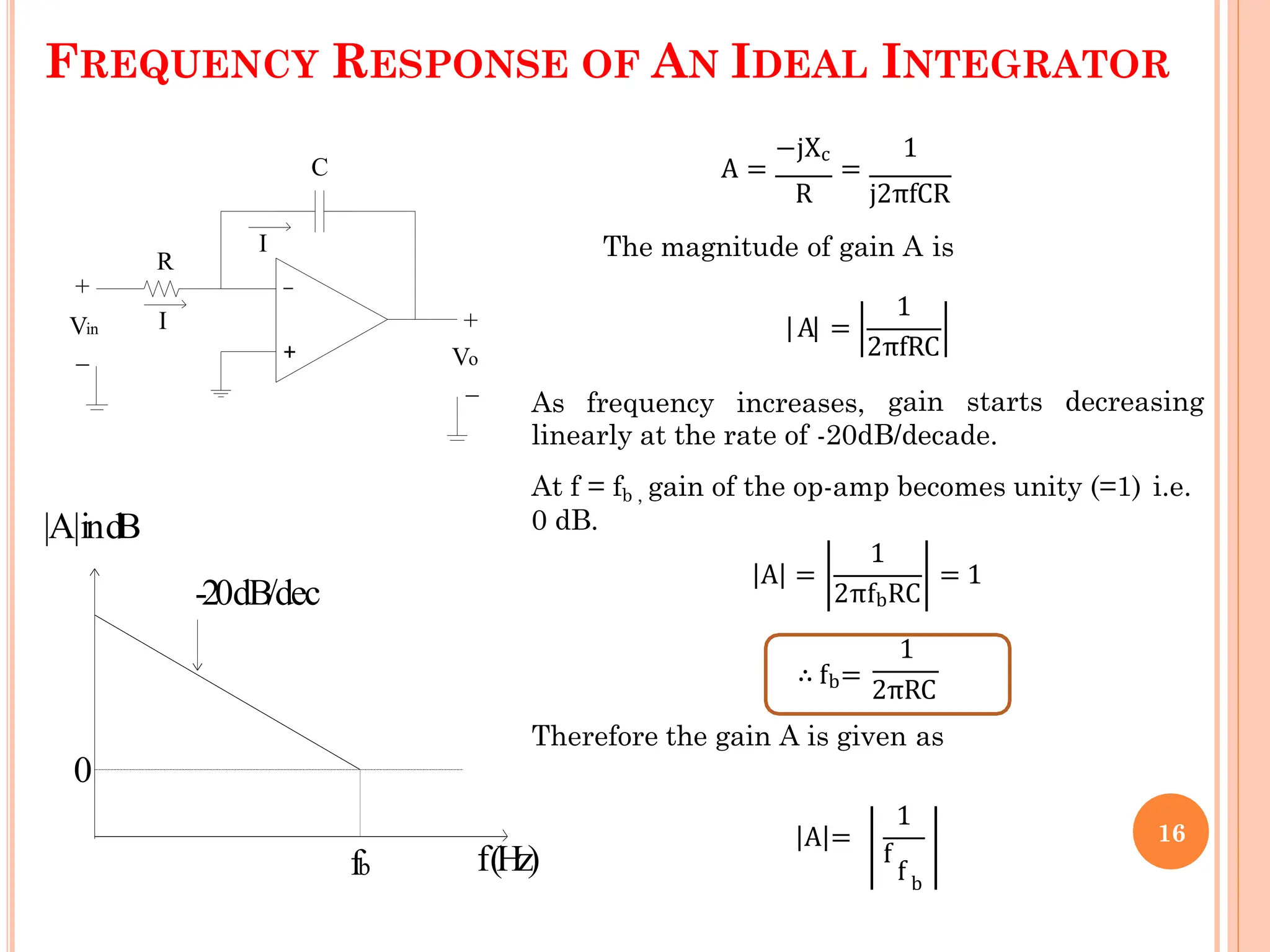


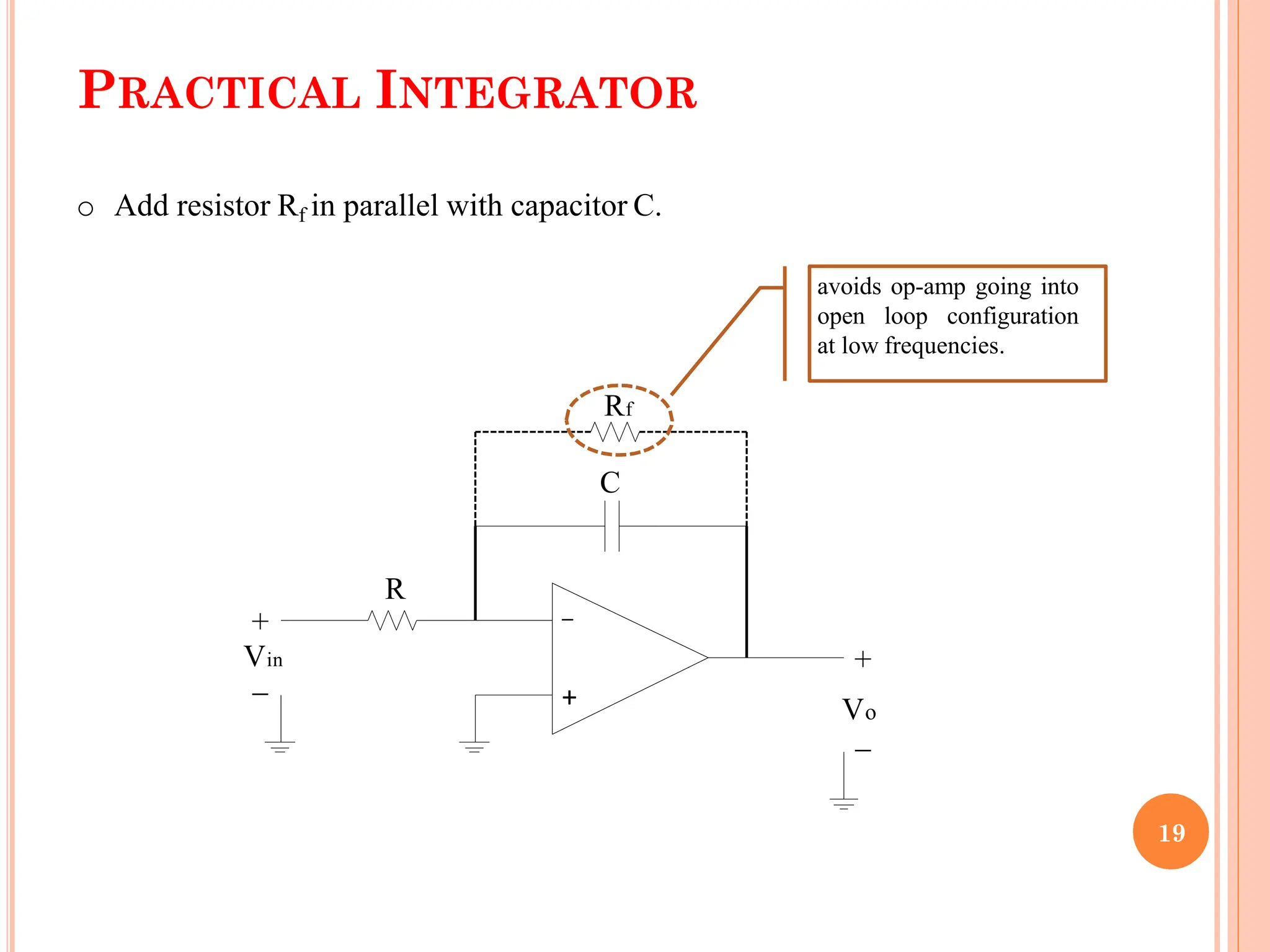
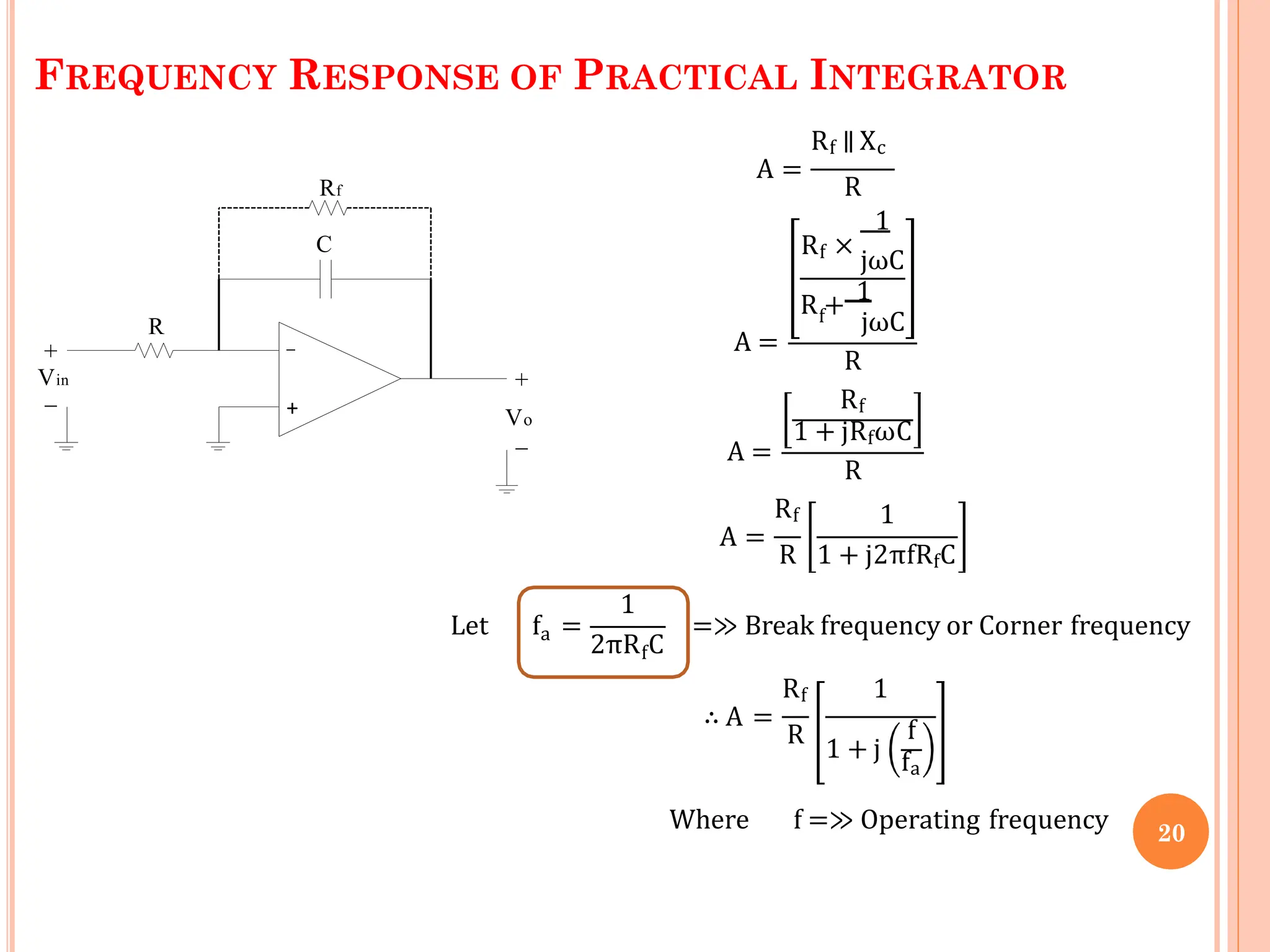
![A =
Rf
R
1
1 +
f
fa
2
Consider the following cases:
1. When f = 0 , the gain A =
Rf
R
−−−− −dc gain
2. When a
0 < 𝑓 < f , the gain A ≅
Rf
R
a
3. When f > f , the gain A ≪
Rf
R
a
4. When f = f , the gain A =
Rf 1
R 2
A = 0.707
Rf
R
fa
|A| in dB
0
-20 dB/dec
fb f (Hz)
Rf
R
-3 dB
[DC gain] 20 log10
True integration is possible over the range
fa < 𝑓 <fb
For better integration fb ≥ 10fa
21](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-21-2048.jpg)
![Prob: Design a practical integrator using Op-Amp IC 741C to satisfy the following
specifications. Assume Vcc = +15V.
1) 3-dB cut-off frequency = 1.5 kHz 2) DC gain = 10
Sketch the frequency response of the circuit.
Sol:
Rf
Given: fa = 1.5 KHz , DC gain = R
= 10
a
f =
1
2πR C
Let
f
C = 0.1µf
∴ 𝐑𝐟 = 𝟏. 𝟎𝟔𝟏𝐤Ω
R
Rf
DC gain = = 10
DC gain = 20log 10
Rf
R
= 20dB
b
f =
fb = 10fa =15kHz
1
2πRC
∴ 𝐑 = 𝟏𝟎𝟔. 𝟏𝟎 Ω
𝐑𝐎𝐌 = 𝐑 ∥ 𝐑𝐟 = 96.4545 Ω
|A| in dB
0
-20 dB/dec
Rf
R
-3 dB
[DC gain] 20 log10
R
Vin
+
_
Rf
C
+
Vo
_
_
+
22
fa fb f (Hz)](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-22-2048.jpg)


![DRAWBACKS OF AN IDEAL DIFFERENTIATOR
o Unstable at high frequencies.[Op-Amp may go into saturation]
o Much Sensitive to noise at high frequencies leading to mis-
amplification of the signal..
The reactance of the capacitor Xc is givenas
1
Xc =
2πfC
As frequency increases, Xc reduces i.e. Capacitor draws more
current from input source.
27](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-27-2048.jpg)









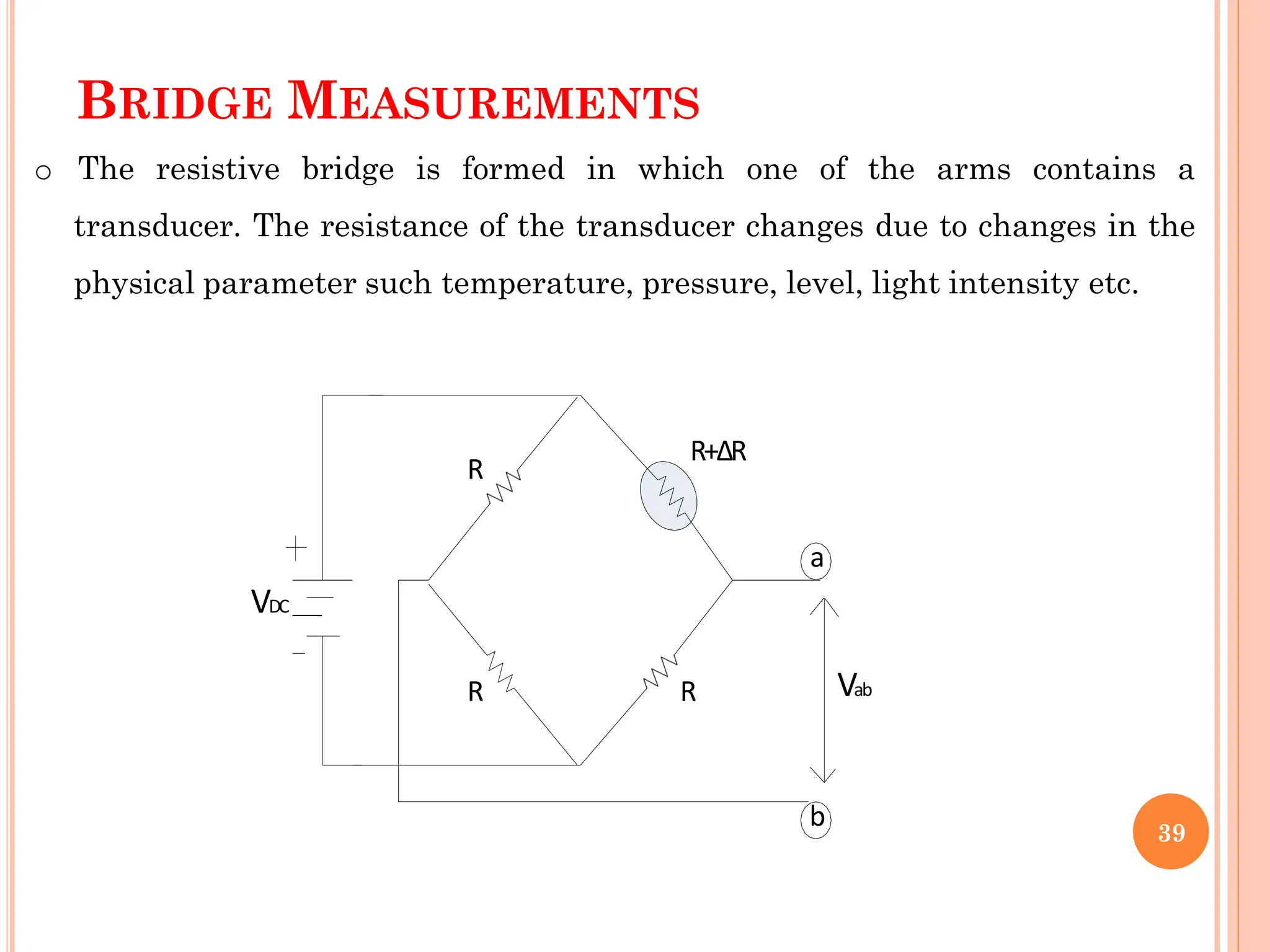
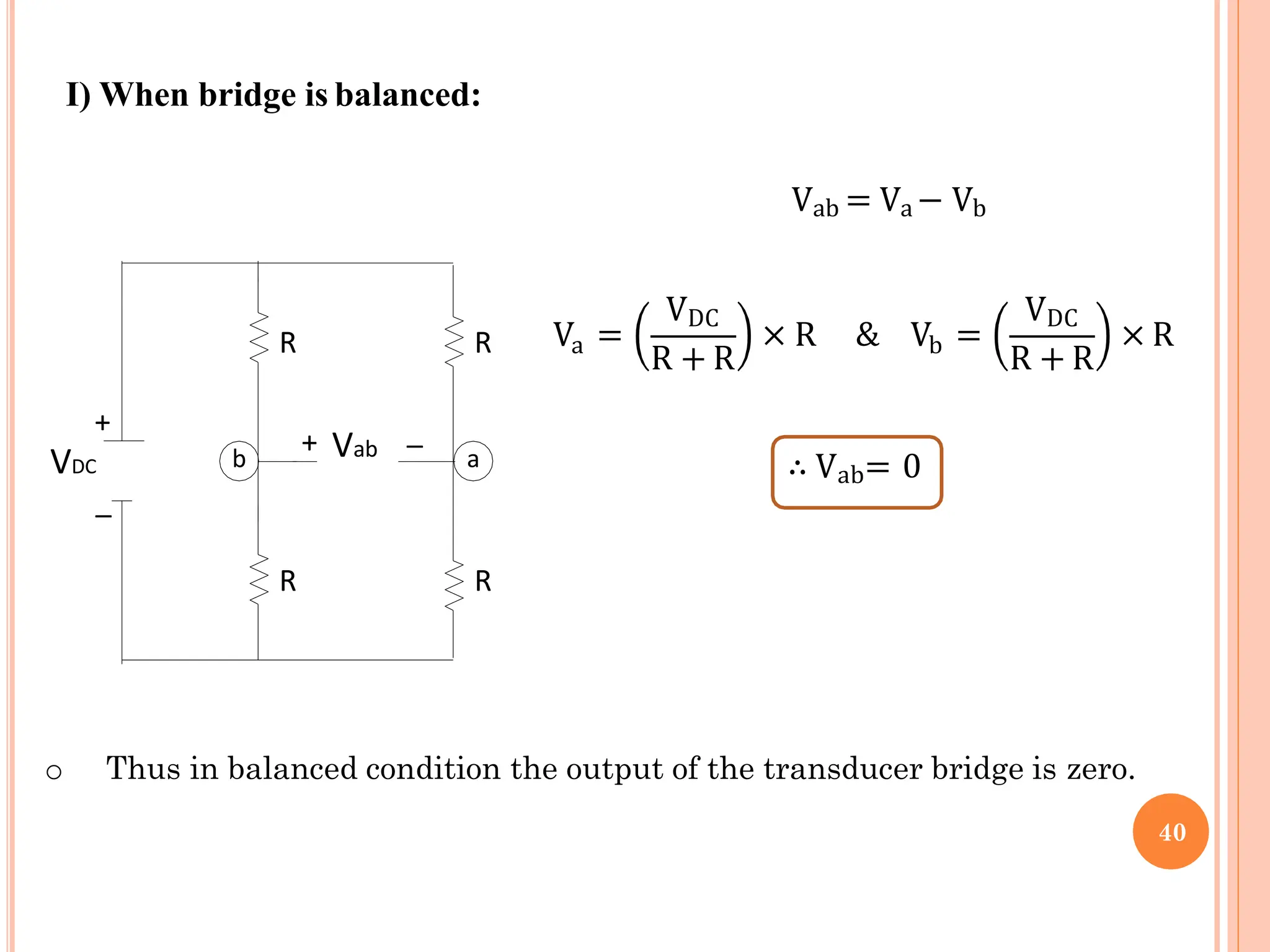
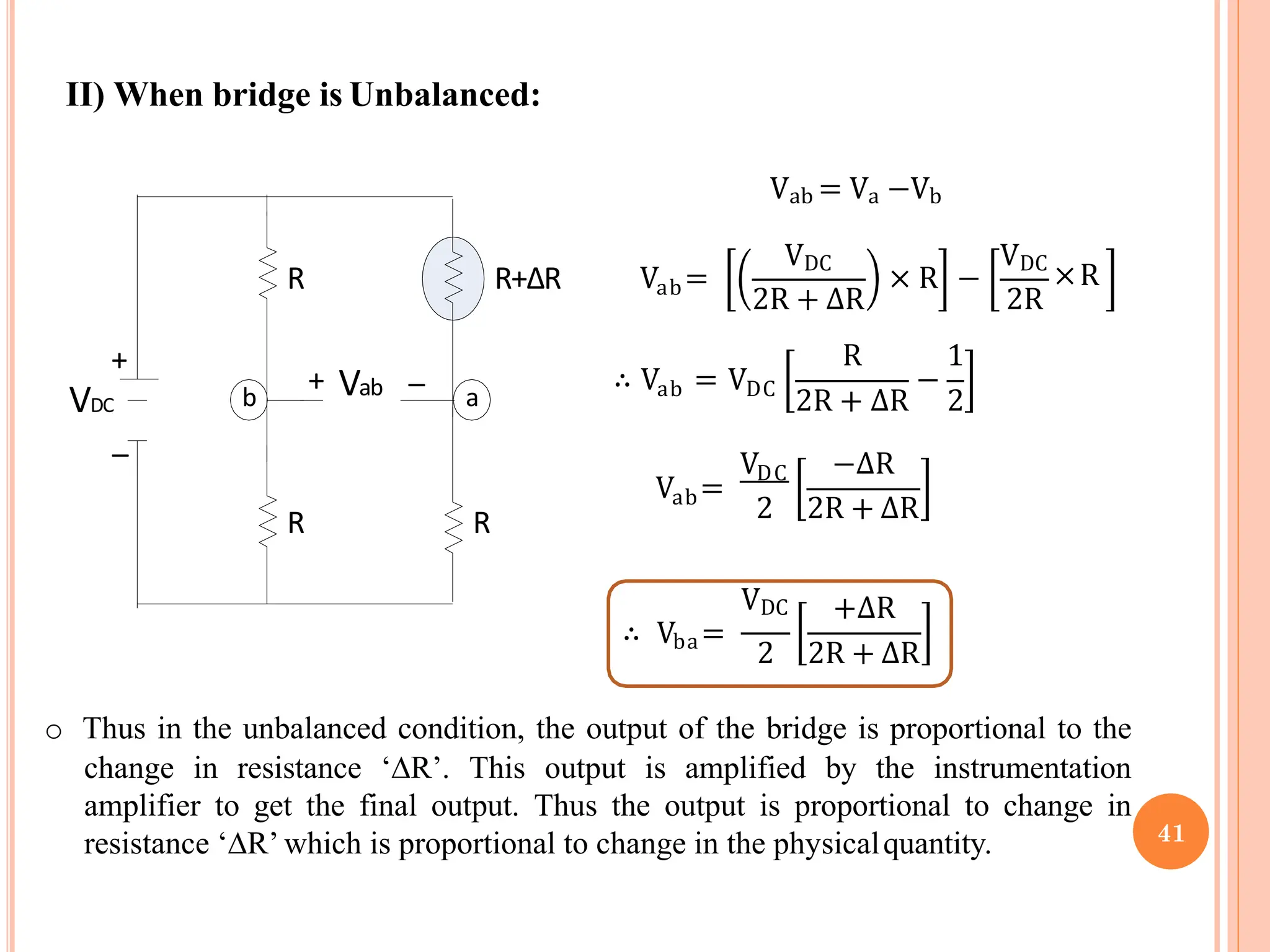
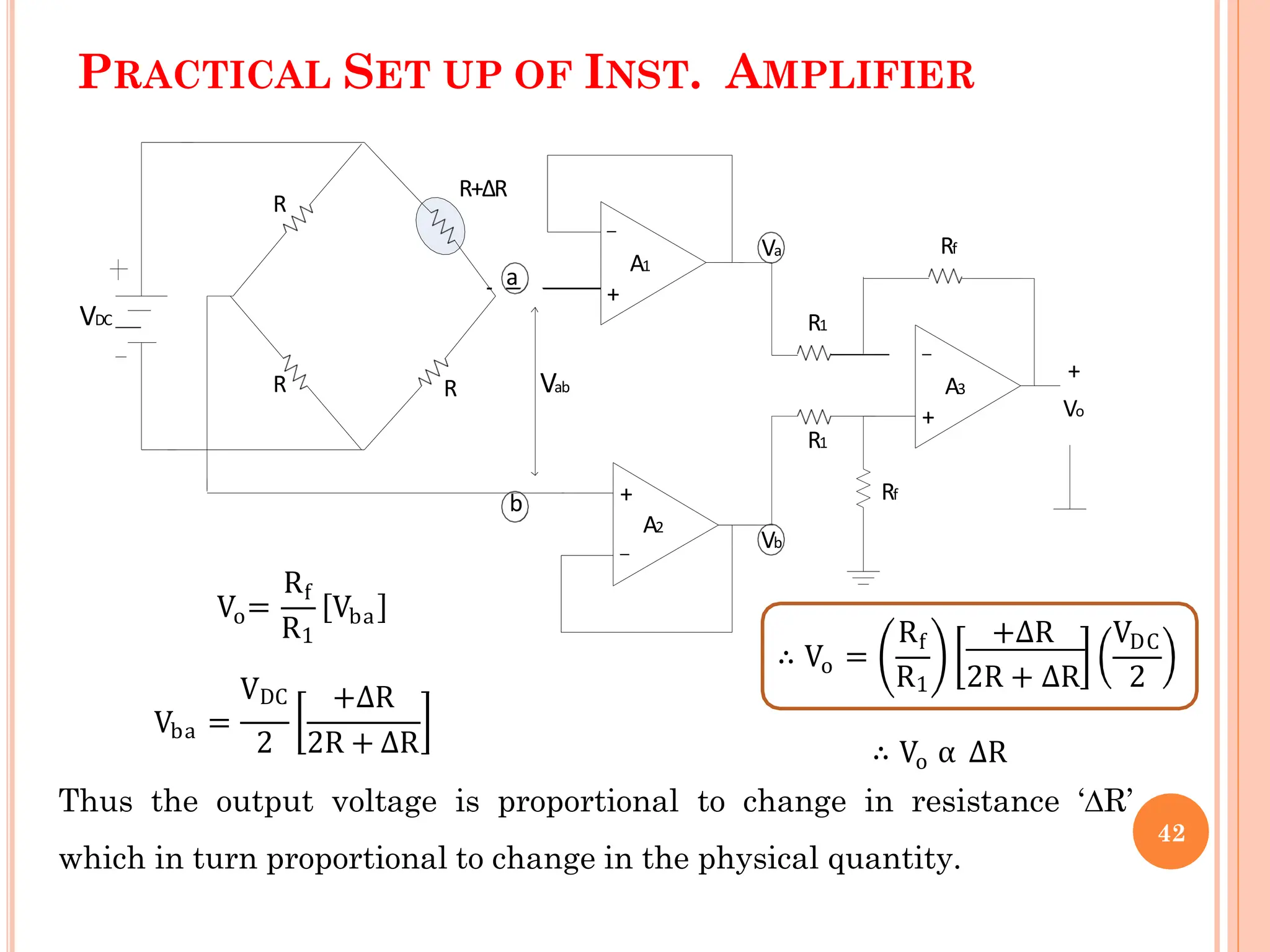




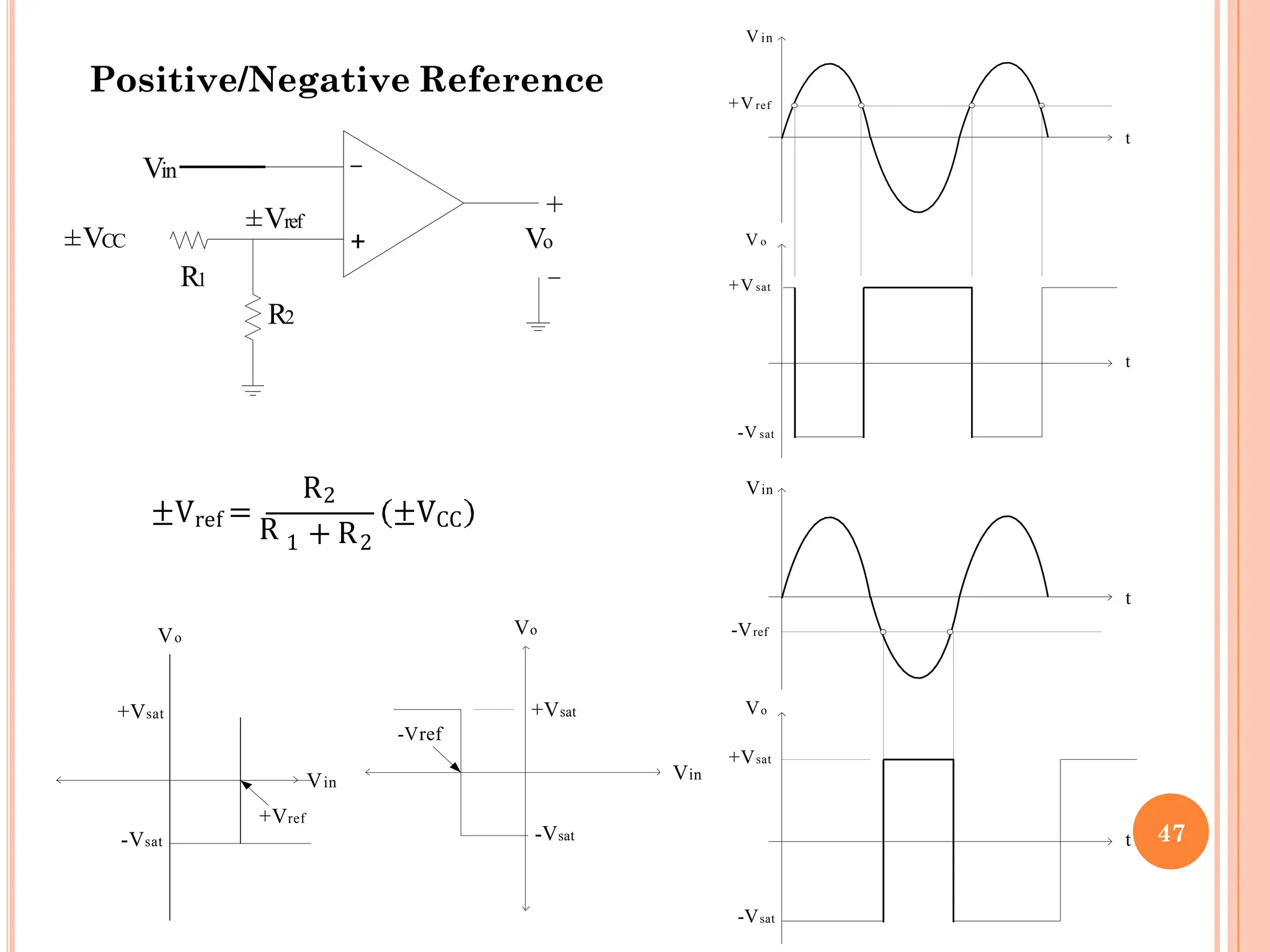





![INVERTING SCHMITT TRIGGER[SYMMETRICAL]
To avoid the false triggering apply a positive feedback and the circuit is
called as Schmitt trigger.
The triggering point VT is calculatedas
T
V =
R2
Vout
When Vin> VT ∴ Vo = −Vsat
When Vin< VT ∴ Vo = +Vsat
Vin
Vo
+Vsat
-Vsat
VUT
VLT
t
t
T
±V =
R1 +R2
R2
R1 +R2
±Vsat 53
+
_
Vin
Vo
+
_
R1
R2
±VT](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-53-2048.jpg)


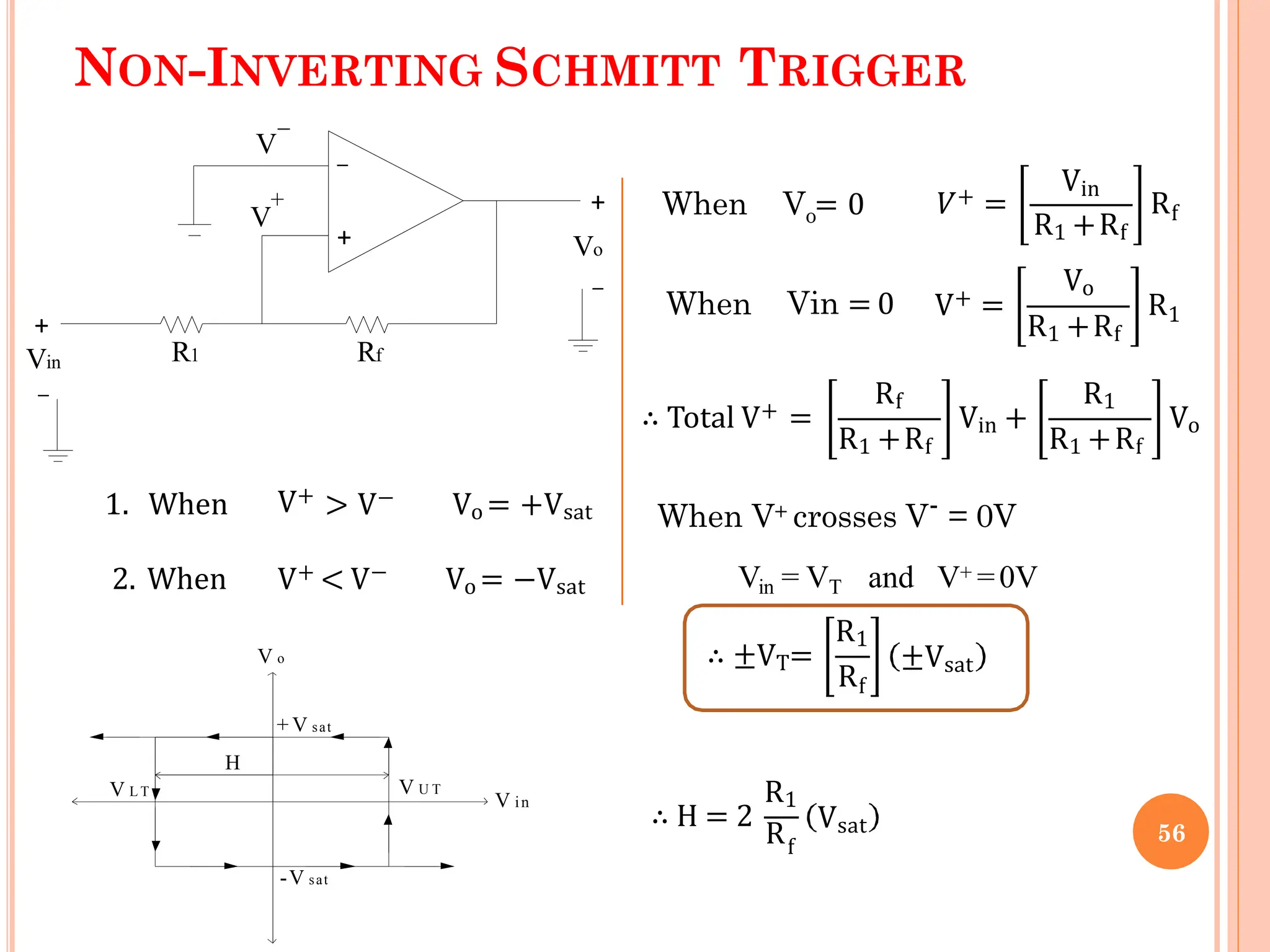
![INVERTING SCHMITT TRIGGER[ASYMMETRICAL]
+
_
R1
Vin
+
_
_
Vo
+
_
V
VT
I R2
+
I
Vo = IR1 + IR2 +V
∴ I =
o
V − V
R + R
1 2
VT = IR2 + V
VT
R1 +R2
o
R R
R1 +R2
= 2
V + 1
V
Vin
Vo
+Vsat
-Vsat
VUT
VLT
t
t
VLT VUT
+Vsat
-Vsat
Vin
H
When
When
Vout = +Vsat
Vout = −Vsat
Vo
, VT = +ve
, VT= − ve
57](https://image.slidesharecdn.com/unit-vop-ampapplicationsfinal-241128053100-67d2dca0/75/UNIT-V_Op-Amp-Applications_Final-sppu-university-57-2048.jpg)