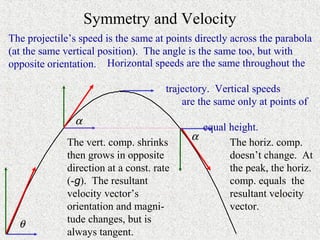
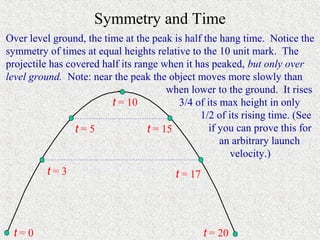
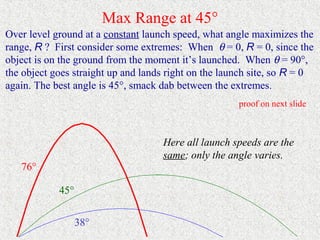
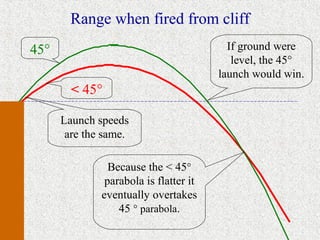
The document discusses projectile motion, describing how objects moving through the air are affected by gravity. It explains that gravity only affects vertical motion, not horizontal motion, so horizontally a projectile maintains a constant velocity if no other forces are present. Examples are provided to demonstrate how to calculate the time of flight, range, and landing point of projectiles fired at various angles and velocities.

1. Motion in Two
Dimensions:
Projectile Motion
Circular Motion
Angular Speed
Simple Harmonic Motion
Torque
Center of Mass

2. Projectile Motion
A red marble is dropped off a cliff at the
same time a black one is shot
horizontally. At any point in time the
marbles are at the same height, i.e.,
they’re falling down at the same rate, and
they hit the ground at the same time.
Gravity doesn’t care that the black ball is
moving sideways; it pulls it downward
just the same. Since gravity can’t affect
horiz. motion, the black particle continues
at a constant rate. With every unit of
time, the marbles’ vertical speed
increases, but their horiz. speed remains
the same (ignoring air resistance).
continued on next slide

3. 9.8 m/s2 Projectile Motion
Gravity’s downward pull is
independent of horiz. motion. So,
the vertical acceleration of each
marble is -g (for the whole trip),
9.8 m/s2 and the sideways acceleration of
each is zero. (Gravity can’t pull
sideways). Whatever horiz.
velocity the black one had when
shot is a constant throughout its
trip. Only its vertical velocity
changes. (A vertical force like
9.8 m/s2 gravity can only produce vertical
acceleration.)
continued on next slide

4. t=0 vy = 0 Projectile Motion (cont.)
t=1
vy = 1
If after one unit of time the
t=2 marbles have one unit of speed
vy = 2 downward, then after two units of
time they have two units of speed
downward, etc. This follows
directly from vf = v0 + a t. Since
t=3 v0 = 0, downward speed is
proportional to time.
vy = 3
Note: The vectors shown are
vertical components of velocity.
The shot marble has a horizontal
component too (not shown); the
dropped one doesn’t.
t=4 vy = 4 continued on next slide

5. t=0 vx = v Projectile Motion (cont.)
t=1 vx
vy Since the shot black marble
v
vx experiences no horiz. forces
t=2 (ignoring air), it undergoes no
vy vy horiz. acceleration. Therefore, its
v horiz. velocity, doesn’t change.
So, the horiz. vector has a
vx constant magnitude, but the
t=3 vertical vector gets longer. The
resultant (the net velocity vector
vy vy in blue) gets longer and points
v more downward with time. When
t = 0, v = vx for the shot marble.
v = vy for the dropped marble for
the whole trip.
continued on next slide
vx
t=4

6. Projectile Motion (cont.)
v
The trajectory of any projectile
is parabolic. (We’ll prove this
later.) If its initial velocity
vector is horizontal, as with the
v black marble, the launch site is
at the vertex of the parabola.
The velocity vector at any
point in time is tangent to the
parabolic trajectory.
Moreover, velocity vectors are
v always tangent to the trajectory
of any moving object,
regardless of its shape.
continued on next slide

7. ∆y = 1
t=0 Projectile Motion (cont.)
t=1
∆y = 3 x=1 The vertical displacements
over consecutive units of
t=2 time show the familiar ratio
x=2 of odd numbers that we’ve
seen before with uniform
∆y = 5
acceleration. Measured
from the starting point, the
t=3 vertical displacements
x=3 would be 1, 4, 9, 16, etc.,
(perfect squares), but the
horiz. displacements form a
∆y = 7 linear sequence since there
is no acceleration in that
direction.
x=4
t=4 continued on next slide

8. Projectile Example
A rifle is held perfectly horizontally 1.5 m over level ground. At the
instant the trigger is pulled, a second bullet is dropped from the tip of
the barrel. The muzzle velocity of the gun is 80 m/s.
1. Which bullet hits the ground first? answer: They hit at same time.
2. How fast is each bullet moving after 0.3 s ? answer:
Use vf = v0 + a t and use vertical info only: v0 = 0, a = -9.8 m/s2,
and t = 0.3 s. We get vy in the pic for each bullet is -2.94 m/s.
Using the Pythagorean theorem for the fired bullet we get 80.054
m/s in a direction tangent to its path. continued on next slide
80 m/s
80 m/s
vy fired bullet vy dropped bullet
after 0.3 s after 0.3 s

9. Projectile Example (cont.)
3. How far away does the fired bullet land (its range)? answer:
The first step is to find the its hang time. This is the same hang time
as the dropped bullet. Use ∆y = v0 t + 0.5 a t 2 with only vertical
data: -1.5 = (0) t + (0.5) (-9.8) t 2. So, t = 0.5533 s.
The whole time the bullet is falling it’s also moving to the left at a
constant 80 m/s. Since horizontally v is constant, we use d = v t
with only horiz. info: d = (80 m/s) (0.5533 s) = 44.26 m.
Note: When a = 0, ∆x = v0 t + 0.5 a t 2 breaks down to d = v t.
80 m/s
1.5 m

10. Projectiles Fired at an Angle
Now let’s find range of a projectile fired with speed v0 at an angle θ.
Step 1: Split the initial velocity vector into components.
v0
v0 sinθ
θ
v0 cosθ
continued on next slide

11. Projectiles Fired at an Angle (cont.)
Step 2: Find hang time. Use ∆y = v0t + ½ a t 2 with
only vertical data:
∆y = (v0 sinθ ) t + ½ (-g)t 2
Over level ground, ∆y = 0. Divide through by t:
0 = v0 sinθ - 4.9 t, and t = (v0 sinθ ) / 4.9
Note: If we had shot the projectile from a 100 m
cliff, ∆y would be -100 m.
v0
v0 sinθ
θ
v0 cosθ continued on next slide

12. Projectiles Fired at an Angle (cont.)
Step 3: Now that we know how long it’s in the air, we know how
long it travels horizontally. (The projectile’s vertical and horizontal
movements are completely independent.) Use ∆x = v0t + ½ a t 2
again, this time with only horizontal data:
∆x = (v0 cosθ ) t + ½ (0) t 2 = (v0 cosθ ) t
This is the same as saying:
v0 horiz. distance = horiz. speed × time
v0 sinθ
In other words, d = v t
θ
v0 cosθ continued on next slide

13. Picklemobile Example
A stuntman drives a picklemobile off a 350 m cliff
going 70 mph. The angle of elevation of the cliff
is 21°. He’s hoping to make it across a 261 m
h wide river and land on a ledge 82 m high. Does
70 mp
he make it ?
Well, the first thing we have to do is convert the
21° initial velocity into m/s:
70 mi 1609 m h
• • = 31.2861 m/s
h mi 3600 s
350 m
continued on next slide
261 m
82 m

14. Picklemobile Example (cont.)
We resolve the initial velocity into components.
11.2119 m/s
Then we find the picklemobile’s hang
/s
61 m time (which is the same as if it had been
31.28
21° shot straight up at about 11.2 m/s), with
29.2081 m/s ∆y = 82 m - 350 m = -268 m.
-268 = 11.2119 t - 4.9 t 2
4.9 t 2 - 11.2119 t - 268 = 0
t = -6.3394 s or 8.6276 s
350 m
(using quadratic formula or computer)
261 m continued
82 m on next slide
continued on next slide

15. Picklemobile Example (cont.)
We want the positive answer for t. The interpretation of the
negative answer is that if the pickle car had been launched from the
height of the ledge, it would have taken
about 6.3 s to reach the edge of the cliff.
29.2081 m/s Anyway, for 8.62757 s the pickle mobile is
in the air and traveling to the right at about
29 m/s. Therefore, its range is
(29.2081 m/s) (8.6276 s) ≈ 252 m < 261 m.
Alas, the poor picklemobile doesn’t make it.
82 m
continued on next slide

16. 11.2119 m/s
Picklemobile Example (cont.)
What max height does the pickle mobile attain?
It attains the same max height as
if it had been shot up at about
11.2 m/s. Since its vertical
velocity is zero at its high pt.,
parabolic we have
trajectory 02 - (11.2119)2 = 2(-9.8) ∆y.
So, ∆y = 6.41 m. Add 350 m
350 m and the max height is 356.41 m.
continued on next slide
82 m

17. Picklemobile Example (cont.)
What is the impact velocity of the pickle
11.2119 m/s
mobile (the velocity upon splash down)?
The horiz. component is the same at landing as it
was on liftoff. We must find the final vertical
29.2081 velocity: vf2 - (11.2119)2 = 2(-9.8) (-350).
m/s So, vf = -83.5805 m/s. 29.2081 m/s
The Pythag. theorem gives us the θ
83.5805 m/s
magnitude of the resultant.
88.5
θ = tan-1 (83.5805 / 88.5371) = 70.74°.
3
350 m Thus the impact velocity is about
71
88.5 m/s at 71° below the horizontal.
m/s

18. Parabolic Proof
A projectile is shot with speed v0 at an angle θ. Its vertical
position is given by y = (v0 sinθ ) t + ½ (-g) t 2. Here y is the
dependent quantity, and t is the independent quantity. Everything
else is a constant.
The projectile’s horizontal position is given by x = (v0 cosθ ) t.
Only x and t are variables, and t = x / (v0 cosθ ). Let’s substitute
this for t in the equation for y:
y = (v0 sinθ ) t + ½ (-g) t 2
y = (v0 sinθ ) [x / (v0 cosθ )] - ½ g [x / (v0 cosθ )]2
g
y = (tanθ ) x - x2
2 v02 cos2θ
The coefficients of x and x 2 are constants. Since the leading coef.
is negative, this is the equation of a parabola opening down.

19. Symmetry and Velocity
The projectile’s speed is the same at points directly across the parabola
(at the same vertical position). The angle is the same too, but with
opposite orientation. Horizontal speeds are the same throughout the
trajectory. Vertical speeds
are the same only at points of
α
equal height.
α
The vert. comp. shrinks The horiz. comp.
then grows in opposite doesn’t change. At
direction at a const. rate the peak, the horiz.
(-g). The resultant comp. equals the
velocity vector’s resultant velocity
orientation and magni- vector.
θ tude changes, but is
always tangent.

20. Symmetry and Time
Over level ground, the time at the peak is half the hang time. Notice the
symmetry of times at equal heights relative to the 10 unit mark. The
projectile has covered half its range when it has peaked, but only over
level ground. Note: near the peak the object moves more slowly than
when lower to the ground. It rises
t = 10 3/4 of its max height in only
1/2 of its rising time. (See
t=5 t = 15 if you can prove this for
an arbitrary launch
velocity.)
t=3 t = 17
t=0 t = 20

21. Max height & hang time depend only on
initial vertical velocity
Each initial velocity vector below has the a different magnitude
(speed) but each object will spend the same time in the air and reach
the same max height. This is because each vector has the same
vertical component. The projectiles will have different ranges,
however. The greater the horizontal component of initial velocity, the
greater the range.

22. Max Range at 45°
Over level ground at a constant launch speed, what angle maximizes the
range, R ? First consider some extremes: When θ = 0, R = 0, since the
object is on the ground from the moment it’s launched. When θ = 90°,
the object goes straight up and lands right on the launch site, so R = 0
again. The best angle is 45°, smack dab between the extremes.
proof on next slide
Here all launch speeds are the
same; only the angle varies.
76°
45°
38°

23. Range Formula & Max Range at 45°
First find the time. Note that ∆y = 0, since the projectile starts and
stops at ground level (no change). ∆y = v0 t + ½ at 2. So,
0 = (v0 sinθ ) t - ½ g t 2 Since the ground is level we divide through
by t giving us t = 2 v0 sinθ / g. Then,
R = (v0 cosθ ) t = (v0 cosθ ) (2 v0 sinθ / g) = 2 v02 sinθ cosθ / g.
By the trig identity sin 2θ = 2 sinθ cosθ, we get R = v02 sin 2θ / g.
Since v0 and g are fixed, R is at a max when sin 2θ is at a max.
When the angle, 2θ, is 90°, the sine function is at its maximum of 1.
Therefore, θ = 45°.
v0
v0 sinθ
θ v0 cosθ

24. Max Range when ∆y ≠ 0
When fired from a cliff, or from below ground, a
projectile doesn’t attain its max range at 45°.
45° is only the best angle when a projectile is fired over
level ground.
When fired from a cliff, a projectile attains max range
with a launch angle less than 45 ° (see next slide).
When fired from below ground, a projectile attains max
range with a launch angle greater than 45 °.

25. Range when fired from cliff
45° If ground were
level, the 45°
launch would win.
< 45°
Launch speeds
are the same.
Because the < 45°
parabola is flatter it
eventually overtakes
45 ° parabola.

26. Ranges at complementary launch angles
An object fired at angle θ will have
75° the same range as when it’s fired at
the same speed at an angle 90° - θ.
Reason: R = 2v02 sinθ cosθ / g, and
the sine of an angle is the cosine of its
complement (and vice versa). For
example, R at 40° is
15° 2v02 sin 40° cos 40° / g
= 2v02 cos 50° sin 50° / g
= R at 50°.
50°
40°

27. Monkey in a Tree
Here’s a classic physics problem: You want to shoot a
banana at a monkey up in a tree. Knowing that the monkey
will get scared and let go of the branch the instant he hears
the sound of the banana gun, how should you aim: a little
above, a little below, or right at him?
Monkey in a tree web site

28. Monkey in a tree explanation
The reason you should aim right at the monkey even though the
monkey lets go right when you pull the trigger is because both
the monkey and the banana are in the air for the same amount of
time before the collision. So, with respect to where they would
have been with no gravity, they fall the same distance.
“gravity-free” monkey
t y
r a vi
tho ut g
i
pa th w monkey w/ gravity
a
ba nan y
h gravit
path wit

29. Homerun Example
From home plate to the center field wall at a ball park is 130 m. When
a batter hits a long drive the ball leaves his bat 1 m off the ground with
a velocity of 40 m/s at 28° above the horizontal. The center field wall
is 2.6 m high. Does he hit a homerun?
s
m/
40 28° 2.6 m
} 1m
130 m
Let’s first check the range to see if it even has a chance:
R = v02 sin 2θ / g = 402 sin 56° / 9.8 = 135.35 m. So, if it can clear
the wall, it will make it. We need to determine its vertical position
when its horizontal position is 130 m. If it’s 1.6 m or more, it’s a
homer. Let’s first find the time when the ball is 130 m away
(horizontally) from the point where it was walloped.
continued on next slide

30. Homerun (cont.)
t = d / v = (130 m) / (40 cos 28°) = 3.68085 s.
Let’s see how high up it is at this time:
∆y = (40 sin 28°) (3.68085) - 4.9 (3.68085)2 = 2.73 m,
which is 3.73 m above the ground, out of the reach of a
leaping outfielder. Therefore, it’s a homer!
In real life the batter wouldn’t be so fortunate. His hit would only
have gone a fraction of the distance with air resistance. What is
barely a homer in a vacuum is a mere blooper in air. Homerun balls
in the major league would go about 700 or 800 ft in a vacuum! This
means balls would routinely be hit out over the stadium into the
parking lot.

31. Trebuchet Example
A trebuchet launches a 180 kg lead sphere at the wall of a medieval
castle 120 m away. The projectile impacts the wall 23 m up. Its high
point in the air occurs 2/3 of the way to the wall. The trebuchet takes
0.6 s to launch the sphere and releases it at a height of 5 m. Find the
launch velocity of the sphere and the average force the trebuchet exerts
on it.
continued on next slide
lead sphere
tree trunk
rope axle
swinging
wheeled wooden frame counterweight
that rolls backwards during
launch
Trebuchet

32. Trebuchet (cont.)
The high pt. occurs horizontally at
a distance of half of what its range (80, h )
would be over level ground,
which is 2/3 of 120 m.
(120, 23)
impact
v So, 80 = R / 2 = v 2 sin 2θ / 2g
⇒ v 2 = 1568 / sin 2θ
v sinθ
θ continued on next slide
v cosθ
(0, 5)

33. Trebuchet (cont.)
Let t = time at impact. Horizontally: 120 = (v cosθ ) t.
Vertically: 18 = (v sinθ ) t - 4.9 t 2. Now substitute for t :
18 = (v sinθ ) [120 / (v cosθ ) ] - 4.9 [120 / (v cosθ ) ] 2
⇒ 18 = 120 tanθ - 4.9 • 14400
v2 cos2θ
From the last slide, v 2 = 1568 / sin 2θ. Substitute for v 2
into the equation above:
14400
18 = 120 tanθ - 4.9 •
1568 • cos2θ
sin 2θ
⇒ 18 = 120 tanθ - 45 sin 2θ ⇒ 6 = 40 tan θ - 15 sin 2θ
cos2θ cos2θ
continued on next slide

34. Trebuchet (cont.)
Now we have an equation with just one variable, but it’s not an easy
one to solve. We can solve for θ by graphing the equation below and
looking for a y-intercept (in radian mode).
15 sin 2θ
y = 40 tanθ - -6
cos θ
2
10
7.5 0.4
5
0.2
2.5
-2.5 0.25 0.5 0.75 1 1.25 1.5 0.525 0.53 0.535 0.54 0.545 0.55
-0.2
-5
-7.5 -0.4
-10 Domain: [ 0, π / 2 ] Domain: [ 0.52, 0.55 ]
180°
θ = 0.5404 radians • = 30.9626°
π radians continued on next slide

35. Trebuchet (cont.)
Now let’s substitute this value for θ into v 2 = 1568 / sin 2θ. This
gives us v = 42.1557 m/s. Using the fact that the trebuchet pushes
on the lead sphere for 0.6 s, we can find the sphere’s acceleration,
(since it starts from rest and we now know vf for the launch
phase).
vf = v0 + a t
aavg = (42.1557 - 0) / (0.6) = 70.2595 m/s2
So, Favg = m aavg = 180 (70.2595) = 12 646.71 N
Because the force (and therefore the acceleration) is not
constant, what we’ve calculated is the average force and
acceleration.

36. Circular Motion
v
v
v
Suppose you drive a go cart in a perfect circle at a constant speed.
Even though your speed isn’t changing, you are accelerating. This is
because acceleration is the rate of change of velocity (not speed), and
your velocity is changing because your direction is changing!
Remember, a velocity vector is always tangent to the path of motion.

37. Tangential vs. Centripetal Acceleration
Suppose now you drive your go cart
15 m/s faster and faster in a circle. Now
your velocity vector changes in
18 m/s finish both magnitude and direction. If
you go from start to finish in 4 s,
your average tangential acceleration
start 10 m/s is:
at = (18 m/s - 10 m/s) / 4 s = 2 m/s2
So you’re speeding up at a rate of 2 m/s per second. This is the rate at
which your velocity changes tangentially. But what about the rate at
which your velocity changes radially, due to its changing direction?
This is your centripetal (or radial) acceleration.
So how do we calculate the centripetal acceleration ? ? ?
Stay tuned!

38. Centripetal Acceleration
Let’s find a formula for centripetal
vf = v
acceleration by considering uniform
circular motion. By the definition of
r v0 = v acceleration, a = (vf - v0) / t. We are
θ subtracting vectors here, not speeds,
r otherwise a would be zero. (v0 and
vf have the same magnitudes.) The
smaller t is, the smaller θ will be,
and the more the blue sector will
approximate a triangle. The blue
vf - v0 vt “triangle” has sides r, r, and v t
(from d = v t ). The vector triangle
vf θ v0 r θ r has sides v, v, and | vf - v0 |. The two
triangles are similar (side-angle-side
similarity). continued on next slide

39. Centripetal Acceleration (cont.)
vf = v
By similar triangles,
v | vf - v0 |
r v0 = v =
r vt
θ
r So, multiplying both sides above
by v, we have
| vf - v0 | v2
ac = =
t r
| vf - v0| vt
(m/s)2 m2 / s2
v r Unit check: = m
v θ r θ m
m
=
s2

40. Centripetal acceleration vector always points
toward center of circle.
v v
ac ac
at
at
moving counterclockwise; moving counterclockwise;
speeding up slowing down
“Centripetal” means “center-seeking.” The magnitude of ac
depends on both v and r. However, regardless of speed or
tangential acceleration, ac always points toward the center. That is,
ac is always radial (along the radius).

41. Resultant Acceleration
The overall acceleration is the
vector sum of the centripetal
acceleration and the tangential
acceleration. That is,
a
a = ac + at
ac at This is true regardless of the
direction of motion. It holds true
even when an object is not
moving counterclockwise
moving in a perfect circle. Note:
while speeding up or The equation above does not
moving clockwise while include v. Vectors of different
slowing down quantities cannot be added!

42. Non-circular paths
Here we have an object moving along the brown path at a constant
speed (at = 0). ac changes, though, since the radius of curvature
changes. At P1 the path is approximated by the large green circle, at
P2 by the smaller orange one. The smaller r is, the bigger ac is.
v2
ac =
r
R2
v
R1
ac P2
ac
ac
P1 v

43. Friction and ac
You’re cruising at a constant 20 m/s
on a winding highway. The radius of
60m curvature where you are is 60 m.
Your centripetal acceleration is:
ac = (20 m/s)2 / (60 m) = 6.67 m/s2
ac 20 m/s The force that causes this acceleration
is friction, which is why it’s hard to
overhead view turn on ice. Friction, in this case, is
the “centripetal force.” The sharper
the turn or the greater your speed, the
greater the frictional force must be.
continued on next slide

44. Friction and ac (cont.)
Since you’re not speeding up, f is the net
force, so Fnet = f = µs N = µs mg = ma.
r We use µs because you’re not sliding (or
even moving) radially. Thus,
f µs mg = ma.
ac v Mass cancels out, showing that your
m
centripetal acceleration doesn’t depend on
overhead view how heavy your vehicle is. Solving for a
we have
a = µs g.
In the diagram N is pointing out of the
slide. Also, a = ac in this case since
at = 0.

45. Centripetal Force, Fc
From F = ma, we get Fc = mac = mv2 / r.
Fc = mv 2
r
If a body is turning, look at all forces acting on it, and find the
net force. The component of the net force that acts toward the
center of curvature (perpendicular to the body’s motion) is the
centripetal force. The component that acts parallel to its
motion (forward or backwards) is the tangential component of
the net force.

46. Forces that can provide a centripetal force
• Friction, as in the turning car example
• Tension, as in a rock whirling around while attached to a
string, or the tension in the chains on a swing at the park.*
• Normal Force, as in a “round-up ride” at an amusement
park (that spins & the floor drops out), or the component of
normal force on a car on a banked track that acts toward the
center.*
• Gravity: The force of gravity between the Earth and sun
keeps the Earth moving in a nearly circular orbit.
• Any force directed toward your center of curvature, such as
an applied force.
* Picture on upcoming slides

47. Simple Pendulum
Two forces act on a swinging pendulum, tension
string of and weight. Tension acts radially. We break the
length L weight vector into a radial component (green)
θ
and tangential one (violet). Blue is bigger than
green, otherwise there would be no net
centripetal force, and the mass couldn’t turn.
Fc = T - mg cosθ = mac = mv2 / L.
T
Ft = mg sinθ = mat
m m
g si Ft is the force that speeds the mass up or slows it
nθ
down. The weight is a constant, but since θ
sθo
θ changes, so do the weight’s components.
mg c
mg cosθ is greatest when the mass is at its low
mg point. This is also where it’s moving its fastest.
For these two reasons T is the greatest when the
mass is at the low point.

48. Facts about the Simple Pendulum
• A pendulum’s period is the same for big arcs as it is for
little arcs, so long as the angle through which it swings
isn’t real large. (The average speed, therefore, is greater
when the arc is bigger, because it must cover a bigger
distance in the same time.)
• The period is independent of the mass.
• The period depends only on the pendulum’s length.
L
• The period = T = 2π (proven in advanced physics)
g
• This formula gives us a way to measure the acceleration
due to gravity (which varies slightly with location) by
measuring the period and length of a pendulum.
• Don’t confuse the symbol T, which is used for both
period and tension.

49. Conical Pendulum
Like a tether ball, the mass
hangs from a rope and sweeps
θ out a circular path, and the rope θ
a cone. θ is a constant. The
vertical component of T
balances mg. The horiz. comp.
of T is the centripetal force.
T
T
ac ac
m m v
v
mg
mg
continued on next slide

50. Conical Pendulum (cont.)
θ All vectors shown are forces.
v points into or out of the slide,
depending on the direction in which
the mass moves. ac is parallel to
T cosθ
T sinθ, which serves as the
centripetal force.
T
θ
T cosθ = mg
m T sinθ T sinθ = mv2 / r
See it in action
mg
Dividing equations: tanθ = v2 / rg

51. Loop-the-loop in a Plane
v A plane flies in a vertical
Ntop circle, so it’s upside down at
mg
the high point. Its speed is
constant, but because of its
nonlinear motion, the pilot
must experience centripetal
acceleration. This ac is
provided by a combination
of her weight and her normal
force. mg is constant; N is
Nbot not. N is the force her
pilot’s chair exerts on her
v body.
mg continued on next slide

52. Loop-the-loop (cont.)
Top: Normal force and weight v
team up to provide centripetal Ntop
force: Ntop + mg = mv2 / r. If mg
the pilot were sitting on a scale,
it would say she’s very light.
r
Bottom: Weight works against
normal force, so N must be
bigger down here to provide the
same centripetal force:
Nbot - mg = mv2 / r. (Fc has a Nbot
constant magnitude since m, v,
and r are constants.) Here a
scale would say that the pilot is v
very heavy.
continued on next slide mg

53. Loop-the-loop (cont.)
The normal force (force on pilot
due to seat) changes throughout
the loop. This case is similar to
the simple pendulum (the only
difference being that speed is
constant here). Part of the weight
opposes N, and the net radial force r
is the centripetal force: θ
N
N - mg cosθ = mac = mv / r 2
θ mg sinθ
We’ve been discussing mg cosθ
the pilot, but what force
mg
causes the plane to turn?
Answer: The air provides the centripetal force on plane

54. B Angular Speed, ω
Linear speed is how fast you move,
measured as distance per unit time.
Angular speed is how fast you
110° A turn, measured as an angle per unit
3m time. The symbol for angular speed
is the small Greek letter omega, ω,
which looks like a curvy “w”.
Units for angular speed include:
degrees per second; radians per
second; and rpm (revolutions per
minute).
Suppose an object moves steadily from A to B along the circle in 5 s.
Then ω = 110° / 5 s = 22° / s. The distance it covers is
(110° / 360°)(2π)(3) = 5.7596 m. So its linear speed is
v = (5.7596 m) / (5 s) = 1.1519 m / s.

55. s Arc length: s = r θ
If θ is in radians, then the arc
length, s, is θ times r. This
θ follows directly from the definition
r of a radian. One radian is the angle
made when the radius of a circle is
wrapped along the circle.
r
When the arc length is as long as 1 radian
the radius, the angle subtended is
one radian. (A radian is really r
dimensionless, since it’s found by
dividing a length by a length.)

56. M´ v = rω
The Three Stooges go to the park.
C´ Moe and Larry are on a merry-go-
round ride of radius r that Larry is
θ pushing counterclockwise, running at
a speed v. In a time t, Moe goes
v/2 from M to M´ and Curly goes from
C C to C´. Moe is twice as far from
v the center as Curly. The distance
M Moe travels is r θ, where θ is in
radians. Curly’s distance is ½ r θ.
s = rθ Both stooges sweep out the same
angle in the same time, so each has
s rθ r θ the same angular speed. However,
= =
t t t since Moe travels twice as far, his
linear speed in twice as great.
v = rω

57. Ferris Wheel Schmedrick is working as a miniature
Problem ferris wheel operator (radius 2.1 m). He
gets a little overzealous and cranks it up
to 75 rpm. His little brother Poindexter
flies out at point P, when he is 35° from
the low point. At the low point the
wheel is 1 m off the ground. A 1.5 m
high wall is 27 m from the low point of
the wheel. Does Poindexter clear the
wall?
P
Strategy outlined on next slide

58. Ferris Wheel Problem-Solving Strategy
1. Based on his angular speed and the radius, 16.4934 m/s
calculate Poindexter’s linear speed.
vx = 13.5106 m/s
2. Break his launch velocity down into vertical
and horizontal components. vy0 = 9.4602 m/s
3. Use trig to find the height of his launch. 1.3798 m
4. Use trig to find the horizontal distance from
25.7955 m
the launch site to the wall.
5. Calculate the time it takes him to go that far 1.9093 s
horizontally.
6. Calculate height at that time. 1.5798 m
7. Draw your conclusion. He just makes it by about 8 cm !

59. Springs
m = mass of weight hanger
and weight. (We’re
assuming the mass of the
spring itself is negligible.)
x x = the amount the spring
stretches due to some force,
in this case the weight mg.
m The amount of stretch (x) depends on how
much force is applied to the spring (mg) and
the stiffness of the spring.
continued on next slide

60. Hooke’s Law: F = - k x
Hooke’s Law says that the stretch
is proportional to the force the
spring exerts, F, which is the
reaction pair to the force causing
the stretch. Here F is mg up, since
the spring is pulling up on the
x weight hanger with a force of mg.
The negative sign is there because
as the spring is stretched
downward, the force it exerts on the
m weight is upward. The constant of
proportionality is the spring
constant, k. The bigger k is, the
stiffer the spring, and the harder it
continued on next slide
is to stretch it.

61. Suppose that to stretch a certain
spring 5 cm, you grab it and pull
Spring Constant, k
with 100 N of force. From
100 N
Hooke’s Law, we get
k = (100 N) / (5 cm) = 20 N / cm. (by hand)
This means for every cm you
want to stretch it, you must apply 5 cm
another 20 N.
Note: k is always positive. In the formula F = - k x,
F is to the right (the direction the spring pulls on your
hand), and x is to the left (the direction in which the
spring was elongated). The minus sign accounts for
this difference in direction.
If you applied different forces and plotted the spring forces
against the corresponding stretches they produced (an F vs.
x graph), what would graph look like?
answer: a line with a slope of -k

62. Simple Harmonic Motion
A mass bobbing up and down on a spring undergoes
simple harmonic motion (SHM). SHM occurs whenever
a body’s position as a function of time is of the form
y = A cos [ b (t - c) ] + d. You’ll see this in trig class too.
y = vertical position (our dependent variable)
t = time (our independent variable)
|A| = amplitude (maximum distance from equilibrium)
d = vertical displacement of the equilibrium from your
reference point (point from which you measure)
m
c = phase shift (time from start of
experiment until the mass reaches equilibrium pt.
its first maximum displacement). c = 0 if experiment starts with
spring fully stretched or compressed. The period of the mass is
the amount of time it takes to bob up and down once. b is used to
determine the period. The period, T, is given by T = 2π / b. 2π is
the “normal” period of the sine & cosine functions (see next slide).

63. sin
Sine & Cosine Graphs: y = A cos [ b (t - c) ] + d
y = cos t 3
2 period = 2π y = 1 cos[ 1(t - 0) ] + 0
1
-Pi Pi } amp = 1 A=1
-2 Pi -1 2 Pi
-2
b=1
-3 c=0
d=0
y = cos t begins at a max; y = sin t begins at
T = 2π / 1 = 2π
equilibrium. Their periods and amplitudes are the
same. Their graphs are congruent, differing only
by a 90° horizontal shift.
period = 2π y = 1 sin[ 1(t - 0) ] + 0
y = sin t 3
2
1
A=1
} amp = 1 b=1
-2 Pi -Pi -1 Pi 2 Pi
c=0
-2
-3
d=0
T = 2π / 1 = 2π

64. Cosine graph: Amplitude y = A cos [ b (t - c) ] + d
3
y = cos t The leading coefficient
2 A=1m
1 determines the amplitude,
-Pi Pi
-2 Pi 2 Pi
which equals |A|. If A is
-1
-2
negative, the graph is
-3 reflected about the time
3
axis. For the red graph,
y = 2 cos t 2
A=2m
1 our mass is pushed up,
compressing the spring
-2 Pi -Pi Pi 2 Pi
-1
2 m and is released at time
-2
-3
zero. In the green graph,
it’s pulled down 1.5 m and
3 released at time zero.
y = -1.5 cos t 2 A = 1.5 m
1
Note: all graphs have the
same period or 2π, and
-2 Pi -Pi -1 Pi 2 Pi none has a phase (horiz.)
-2
shift or a vertical shift.
-3

65. Cosine graph: Period y = A cos [ b (t - c) ] + d
3 T = 2π / b
y = cos t 2 2π
1 The bigger b is, our
-Pi Pi
“scrunch factor,” the more
-2 Pi 2 Pi
-1
scrunched up the graph
-2 b = 1 s-1
-3 gets. The red graph
completes 3 cycles in same
y = cos 3 t 3
2π / 3
2 time the blue graph does
1 one, and red’s period is 3
-2 Pi -Pi -1 Pi 2 Pi times shorter. So, the mass
-2
b = 3 s-1 in the red graph goes up and
-3 down 3 times more often.
3 The green graph completes
y = cos 0.5 t 2 half as many cycles as blue
1 b = ½ s-1 and its mass has twice the
-2 Pi -Pi -1 Pi 2 Pi period. Note: b’s units
-2 cancel t’s.
4π
-3

66. Cosine graph: vertical displacement y = A cos [ b (t - c) ] + d
3
y = cos t 2 Adding or subtracting
-Pi
1
Pi outside of the cosine
-2 Pi -1 2 Pi function shifts the graph
-2
d=0 vertically. The dotted
-3 lines are lines of
y = cos t + 1.5 3 symmetry. For our mass
2
on a spring, this is where
1
it’s in equilibrium (where
-2 Pi -Pi -1 Pi 2 Pi the spring is neither
-2 d = 1.5 stretched nor compressed).
-3
For the red graph, the
3 mass is in equilibrium 1.5
y = cos t - 0.5 2 d = -0.5 meters above the point
1
from which we chose to
-2 Pi -Pi -1 Pi 2 Pi
make our measurements.
-2
-3

67. Cosine graph: Phase Shift y = A cos [ b (t - c) ] + d
3
y = cos t 2 Adding or subtracting inside
1 c=0 the cosine function shifts the
-2 Pi -1 2 Pigraph horizontally. (Adding
-2 shifts it left, subtracting
-3 right.) Like the mass in the
c = -1.2 s 3 blue graph, the red mass was
y = cos (t + 1.2)
2
compressed 1 m and then
}
1
released, but the clock was
-2 Pi -Pi -1 Pi 2 Pistarted 1.2 s after it had
-2 reached max compression.
-3
The green mass was also
3 c = 0.9 s compressed 1 m and
y = cos (t - 0.9) 2
released, but the clock was
}
1
started 0.9 s before the mass
-2 Pi -Pi Pi 2 Pi
-1
reached max compression.
-2
-3

68. SHM / Spring Problem part 1
Schmedrick wants to go bungee jumping but can’t afford it, so he takes
a dive off a bridge 60 ft over a ranging river with a giant slinky
connecting him to the bridge. After the leap he begins bobbing up and
down. While bobbing, he’s moving the fastest when he’s 27 ft above
the river. He gets as high as 39 ft above the river. It takes him 5 s to
go from his high point to his low point. Schmedrick weighs 105 lb, and
the natural length of the slinky is 20 ft.
1. What’s the spring constant of the slinky?
The point at which Schmedrick is moving the fastest while bobbing is
the equilibrium point. (v = 0 at the high and low points and v is a max
half way in between.) This happens at 27 ft above the river, which is
60 - 27 = 33 ft from the bridge. So, if Schmed were just hanging from
the slinky, his weight would stretch it 33 - 20 = 13 ft. Thus,
k = (105 lb) / (13 ft) = 8.08 lb / ft. This means every foot of stretch
requires about an additional 8 pounds of force.

69. bridge
SHM / Spring Problem part 2
y = 60 ft
2. If the clock starts when he jumps off the bridge, write
Schmedrick’s position as a function of time using the river
as a reference point.
Ignoring air resistance, a mass on a spring undergoes
SHM (derived in advanced physics). Hence we can use
y = A cos [ b (t - c) ] + d. Our task, then, is to find H y = 39 ft
A, b, c, and d. d = 27 ft since the equilibrium pt, Eq,
is 27 ft above our reference position. The high pt, H, is
Eq y = 27 ft
given to be 39 ft. This is 12 ft above Eq, so A = 12 ft,
and the low pt, L, is 12 ft below Eq. Since it takes 5 s
for him to go from H to L, his period is 10 s. So, L y = 15 ft
T = 2π / b ⇒ b = 2π / (10 s) = 0.628 s-1. If Schmedrick
had been at H or L at t = 0, c would be zero. But the clock
starts early (when y = 60 ft), so let’s figure out
how long it takes him to fall to H (assume free fall). y=0
continued on next slide river

70. bridge
SHM / Spring Problem part 2 (cont.)
If we’d like to continue working in feet, we can’t use y = 60 ft
9.8 m/s2 for g. Instead we use its equivalent: 32 ft / s2.
He falls 21 ft to H. Thus, -21 = (0) t + 0.5 (-32) t 2
⇒ t = 1.146 s, and this is our c value. (This is only
an approximation, since the spring begins stretching after
he falls 20 ft.) Putting it all together, we have:
H y = 39 ft
y(t) = 12 cos [ 0.628 (t - 1.146) ] + 27
where t is the time in seconds from the instant he
jumps, and y is his height above the water in feet. Eq y = 27 ft
Note: This formula only works for t > 1.146 s, since
that’s when SHM begins.
L y = 15 ft
Check by plugging in some values into the function
(using radian mode in the calculator):
y(1.146) = 12 cos [0] + 27 = 12(1) + 27 = 39 ft. (H)
y(6.146) = 12 cos [0.628 (5) ] + 27 = 12 (-1) + 27 y=0
= 15 ft. (L) So he’s at L 5 s after he’s at H. river

71. SHM / Spring Problem parts 3 & 4
3. How high up is Schmedrick 14 s into the experiment?
y (14) = 12 cos [0.628 (14 - 1.146) ] + 27 = 24.4 ft. (When we
calculated b, we used 2π rather than 360° for the “normal” period
of the cosine function, so we must put our calculators in radian
mode.)
4. At what times is he 30 ft above the river?
He can only be at one position at a particular time, but he can be at a
particular position at many different times. (This is the nature of a
function.) Thus, 30 = 12 cos [ 0.628 (t - 1.146) ] + 27, and we must solve
for t. First isolate the cosine function by subtracting 27 and dividing by
12: 0.25 = cos [0.628 (t - 1.146) ]. Think of the quantity in the
brackets as an angle. We want to know what angles have a cosine of
0.25. One angle is cos-1 (0.25) = 1.318 (radians). But this is only one
of an infinite number of angles whose cosine is 0.25.
continued on next slide

72. y
SHM / Spring Problem part 4 (cont.)
P1 On a unit circle (radius 1, center at origin):
cosθ left & right (green)
sinθ up & down (brown)
θ
x tanθ slope (of red)
One angle in which cosθ = 0.25 is 1.318
radians ≈ 75.5° (in Q I). Another
occurs at 4.965 ≈ 284.5° (in Q IV). To
P2 get to P1 or P2 from the origin, you must
go 0.25 units to the right. Thus, both
angles have the same cosine of 0.25. Negative angles and angles over
2π (or 360°) that terminate at P1 or P2 will also have a cosine of 0.25.
These angles are 1.318 + 2nπ and 4. 965 + 2nπ, where n = 0, ±1, ±2,
±3, …. Ex: when n = 5, cos[1.318 + 2(5)π ] = 0.25. Here we’ve gone
around the circle 5 times and stopped at P1. continued on next slide

73. SHM / Spring Problem part 4 (cont.)
We are in the process of solving 0.25 = cos [0.628 (t - 1.146) ]. Our
“angle” is 0.628 (t - 1.146). Therefore,
0.628 (t - 1.146) = 1.318 + 2nπ t = 1.146 + (1.318 + 2nπ) / 0.628
or or
0.628 (t - 1.146) = 4. 965 + 2nπ t = 1.146 + (4.965 + 2nπ) / 0.628
We only want t values > 1.146 s (when SHM begins). Substituting in
for n, we get t = 3.245 s, 13.250 s, 23.255 s, … or
t = 9.052 s, 19.057 s, 29.062 s, …
These are all the times when Schmedrick is 30 ft above the water. The
top row lists times when he’s on his way down. The bottom row lists
times when he’s bouncing back up. The difference between consecutive
times on a given row is 10 s (neglecting some slight compounded
rounding error), which is the period of his motion. That is, every 10 s
he is at the same position moving in the same direction.

74. SHM / Spring Problem part 5
We’ve been neglecting air resistance throughout this problem. How
would Schmedrick’s position vary with time in real life?
It’s not exactly SHM any more, but it’s similar. He will still bob up and
down relative to the same equilibrium point. It would take him a little
longer to fall to the high point for two reason. One, drag from the air
slows him down. Two, after falling 20 ft (natural length of the slinky)
the slinky begins to stretch out and exerts an upward force on him,
slowing him down. This would change our c value. The most
interesting change, however, is the amplitude. In real life, the amplitude
itself is a function of time, diminishing with each bounce due to air
resistance and friction in the slinky. This is damped periodic motion.
Let’s checked out some graphs of Schmedrick’s motion, damped (real
life) and undamped (idealized simple harmonic motion).
continued on next slide

75. SHM / Spring Problem part 5 (cont.) In real life drag forces
would decay his
50
undamped amplitude until he’s
40 hanging at the equilibrium
30
point 27 ft above the
water, barely moving.
20
The amplitude decays
10 exponentially, meaning
that a certain percentage
50
10 20 30 40 50
of it is lost with each
bounce. The percentage
40
lost depends on the
30 viscosity of the fluid in
which the mass is
20
moving. The damping
10 damped would be more severe in
water than in air.
10 20 30 40 50

76. Things that undergo SHM
• Mass bobbing vertically from a spring w/ no air resistance
• Mass on a frictionless floor attached to a spring on the wall
• Simple pendulum or person on a swing where max displacement is
not excessive
• The shadow on a wall of an object moving in a vertical circle at
constant speed with light shining on it from the side
• A person who jumps into a tunnel that goes clear through the
center of the Earth all the way to the opposite side
All of these situations have common features:
• periodic motion with constant period
• an equilibrium point half way between its high and low (or leftmost and
rightmost) points where its moving its fastest
• a constant amplitude that is half of its total span (from high to low)
• a “restoring force” that always acts in the direction of equilibrium and is a max
at the extremes (max distance from equil.)

77. Torque
r F
9/16
Acme Nut Buster
Informally speaking, torque is the measure of a force’s turning power.
Normally it’s impossible to loosen a nut or bolt by hand. A wrench
doesn’t make you any stronger, but it increases your turning power,
because the farther a force is applied from the axis of rotation, the
greater the torque it produces. So long as F and r are perpendicular,
the magnitude of the torque is given by τ = r F, where r is the
magnitude of the displacement vector from the center of rotation to the
point of application of the force. Technically, torque is a vector
quantity, but we’ll mainly deal with its magnitude.

78. Torque when force is at an angle
F sinθ F
r θ
9/16 F cosθ
Acme Nut Buster
When F is not perpendicular to r, we can split F into components.
The component parallel to r does nothing in the way of turning the
bolt, so it produces no torque. The perpendicular component does
produce torque. Therefore, our general formula for the magnitude of
torque is:
τ = r F sinθ

79. Torque as a vector
Torque is a vector quantity that can be defined relative to any
point of interest by the cross product:
τ = r ×F
where r is the displacement vector from the point of interest to the
point of application of the force. As you learned in the last unit, the
magnitude of r × F is r F sinθ, where θ is the angle between
r and F. Use the right-hand rule to find the direction of τ . In
the wrench example, τ points out toward you, perpendicular to
both r and F. The torque vector does not point in the direction of
motion, as a velocity vector does. Just as a net force produces
acceleration (a change in velocity), a net torque produces angular
acceleration (a change in angular speed).
F
θ r

80. How much do
I weigh?
See-saw Example part 1
175 lb
35 lb
7 ft 5 ft fulcrum 6 ft
A man, a turtle, and a bike rider are positioned on a giant see-saw as
shown. If the see-saw is in equilibrium, how much must the man weigh?
Answer: The torque that would produce clockwise rotation (from the
weight of the bike and rider) must cancel out the torques that would
produce counterclockwise rotation (from the man and turtle). If the
man’s weight is W, then
(7 ft) W + (5 ft) (35 lb) = (6 ft) (175 lb)
(7 ft) W = 875 ft·lb W = 125 lb

81. See-saw Example part 2 175 lb
35 lb
7 ft 5 ft 6 ft
The see-saw is in equilibrium at this instant, but which side will go
down after a short time?
Answer: Because the biker is heavier and, presumably, moving faster
than the turtle, the torque he produces will diminish much more quickly
than the torque the turtle produces. Therefore, the turtle’s side of the
see-saw will go down. Note: A foot-pound is a unit of torque (a force
times a distance). The SI unit for torque is the Newton-meter (N m).
Also note that the angle θ in the formula τ = r F sinθ is 90° for each
person/animal since each weight vector is ⊥ to its corresponding
displacement vector from the fulcrum.

82. Equilibrium
N = 335 lb
35 lb
175 lb
125 lb
N is the normal force--the force on the see-saw due to the fulcrum. Its
magnitude is the sum of the weights of the 3 see-saw participants. If
this were not the case, the see-saw would be accelerating either up or
down. So, equilibrium means no net force and no net torque.
Note that weights on each side don’t have to be equal. The distance
each weight lies from the fulcrum must be taken into account.

83. Center of Mass
c. m. for weight
beam
Schmedrick decides to build his own see-saw, but of course he screws
up, and instead of putting the fulcrum in the middle, he puts it only 1/ 3
of the way from the right end. The beam of the see-saw has a mass of
50 kg. If the beam is uniform (equal density throughout), then we
pretend all of the weight of the beam acts right at the center of the
beam. This point is called the center of mass because it’s the point
where the beam would balance if the fulcrum were beneath it. Schmed
figures, rather than cutting some of the left end off, he could attach a
weight at the right end. In order to attain a balance, the center of mass
of the weight-beam system must be shifted to the right, so that it is right
above the fulcrum. How much weight should he add?
continued on next slide

84. Center or Mass (cont.)
m
x=0 c. m. for
beam x = L/2 x = 2L/3 x=L
To calculate the center of mass, we set up a coordinate system. (The
reference point doesn’t matter.) For our purposes, all 50 kg of the
the beam is right at the its center of mass (at L / 2). Mathematically,
the center of mass for a system of masses is given by adding up all
the products of mass and position and then dividing by the total
mass: 50 (L / 2) + m (L )
xcm = = 2L/3
50 + m
The L’s cancel 25 + m 2 75 + 3 m = 100 + 2 m
=
out and we have: 50 + m 3
So, m = 25 kg, and its weight is (25 kg) (9.8 m/s2) = 245 N

85. Center of mass is independent of coordinate system
m
x=L c. m. for x=0
x = -2L / 3 beam x = L/2 x = L/3 x = L/3
x = -L / 6 x = 0
Let’s show we get the same answer using different coordinate systems:
one with zero at the right end where positive is to the left (red); and
one with zero at the fulcrum where positive is to the right (black). In
each equation we set the center of mass equal to the fulcrum’s position
in that coordinate system:
50 (L / 2) + m (0 ) 50 (-L / 6) + m (L / 3)
xcm = = L/3 xcm = = 0
50 + m 50 + m
In each case m comes out to be 25 kg, as it was on the last slide.
(Work the algebra out for yourself.) This would be true no matter what
coordinate system we chose.

86. Torque Method L/6 L/3
m
c. m. for
beam
mg
50 g
Same problem, another method: This time we’ll find m using torque.
In order for the beam to balance where the fulcrum is, the torque
(force × distance) must cancel out on each side of the fulcrum. The
entire weight of the beam acting at its center of mass is equivalent to its
weight being spread out along its length.
50 g (L / 6) = m g (L / 3) Both g and L cancel out and m = 25 kg,
just as it did on previous slides. (Since the weight of the beam acts at
half the distance as the weight of the green mass, the green mass must
have half the weight.)