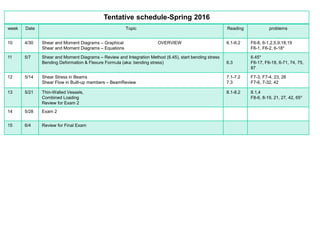
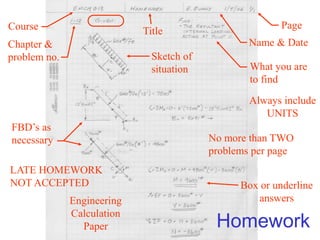
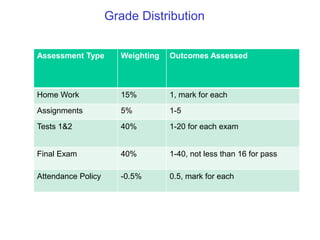
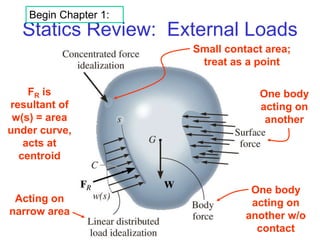
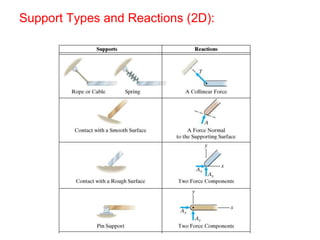
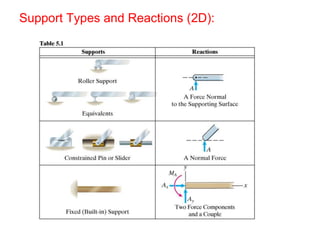
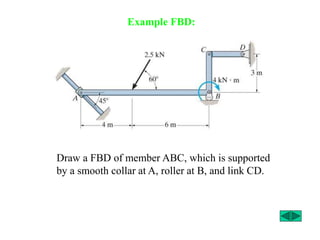
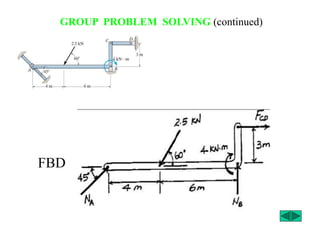
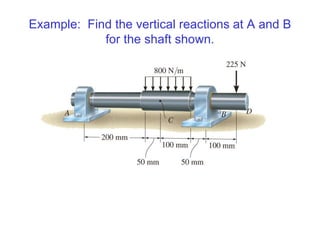
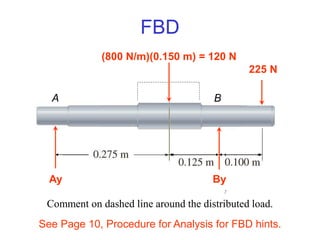
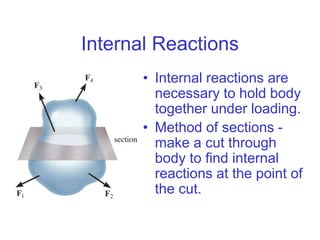
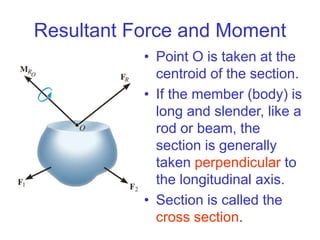
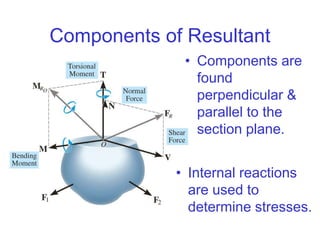
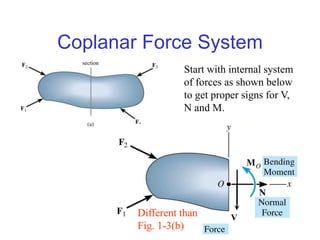
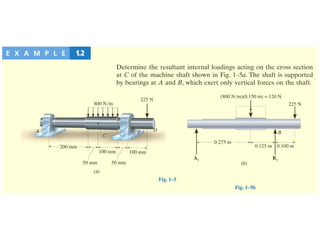
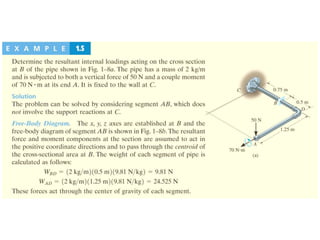
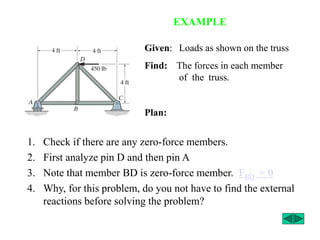
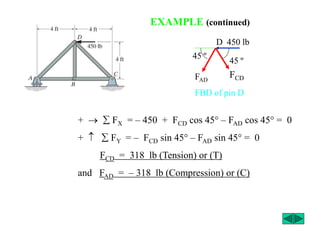
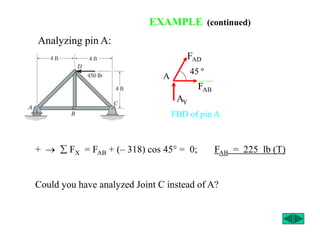
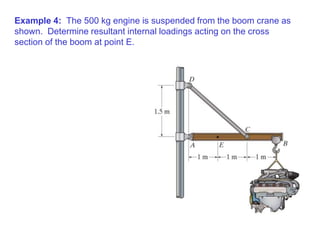
The document outlines the syllabus and structure of a strength of materials course taught by Dr. Hamed Abdulgader Dow, detailing the schedule, reading assignments, homework guidelines, and course objectives for Spring 2016. It covers fundamental concepts such as external loads, internal reactions, static equilibrium, stress analysis, and provides examples of free-body diagrams and internal force calculations. The document aims to prepare students for practical engineering applications while assessing their understanding through assignments and examinations.

1. Arch-E 162 –Strength of Materials
Reference Book.
 Course Lecturer: Dr. Hamed Abdulgader Dow
 Email: Agassi78@gmail.com,
 Tel. No. : 00218944233827
Lecture #1.

2. Today…
• Introduction
• Syllabus
• Homework
• Course Objectives
• Statics review

3. SEE Syllabus – Key Points:
• HW Guidelines
• Tentative schedule
• Grade Distribution
• COURSE OBJECTIVES

4. Schedule – reading and HW assignments:
Tentative schedule-Spring 2016
problemsReadingTopicDateweek
F1-1, F1-3, 1-1, 3, 10*, 181.1-1.2Introduction, Statics Review, Internal Reactions REVIEW STATIC PROBLEMS!!3/51
F1-11, F1-12, 1-21, 32, 45,
51, 61*
,F1-19, F1-21, F1-22, 1-77
1.3-1.7Direct Stress (Average Normal, Average Shear),
Bearing stress, Allowable Stress, Simple Connections
3/122
F2-1, 2-3, 6, 132.1-2.2Strain (Normal and Shear), (also review stress – shear, normal, FS via simple connection)3/193
F3-8, 3-17, 253.1-3-8Mechanical Properties of Materials, Hooke's Law (also Poisson’s Ratio)3/264
F4-1, 4-5,10*,68,704.1,4.2,4.6Axial Deformation Thermal Expansion & Stress4/25
4-87,884.7Stress Concentrations, Start Chapter 54/96
F5-1, F5-4, 5-1, 5, 14
5-31, 37, F5-7, 5-60
5.3-5.1
5.4
Torsional Deformation & Torsion Formula
Power Equation for Torsion, Angle of Twist
4/167
1205.8Stress Concentrations (torsion)
Exam 1 review: More Practice Problems: Ch1 Direct Stresses, Poisson’sRatio
,Chapter4 deformation, Chapter 5 Torsion
4/238
Exam 19

5. Tentative schedule-Spring 2016
problemsReadingTopicDateweek
F6-8, 6-1,2,5,9,18,19
F6-1, F6-2, 6-18*
6.2-6.1Shear and Moment Diagrams – Graphical OVERVIEW
Shear and Moment Diagrams – Equations
4/3010
6.45*
F6-17, F6-18, 6-71, 74, 75,
87
6.3
Shear and Moment Diagrams – Review and Integration Method (6.45), start bending stress
Bending Deformation & Flexure Formula (aka: bending stress)
5/711
F7-3, F7-4, 23, 26
F7-6, 7-32, 42
7.2-7.1
7.3
Shear Stress in Beams
Shear Flow in Built-up members – BeamReview
5/1412
8.1,4
F8-6, 8-19, 21, 27, 42, 65*
8.1-8.2Thin-Walled Vessels,
Combined Loading
Review for Exam 2
5/2113
Exam 25/2814
Review for Final Exam6/415

6. Homework
Name & Date
What you are
to find
PageCourse
Chapter &
problem no.
Engineering
Calculation
Paper
Box or underline
answers
Sketch of
situation
FBD’s as
necessary No more than TWO
problems per page
Title
Always include
UNITS
LATE HOMEWORK
NOT ACCEPTED

8. Outcomes AssessedWeightingAssessment Type
1, mark for each15%Home Work
1-55%Assignments
1-20 for each exam40%Tests 1&2
1-40, not less than 16 for pass40%Final Exam
0.5, mark for each-0.5%Attendance Policy
Grade Distribution

9. Mechanics of Materials
• External Loads produce Internal Loads
• Internal Loads cause a body to deform
• Internal Loads cause stress
• How much does body deform?
• How much stress?
• Is it Safe at this stress?
• How big should it be so stress is low
enough?

10. Course Outcomes 1
• Solve axially loaded members for stresses and
deflections in statically determinate or
indeterminate cases including thermal stresses.
• Solve torsionally loaded shafts for stresses and
deflections in statically determinate or
indeterminate cases.
• Solve beams under bending for stresses.
• Solve transversely loaded beams for internal shear
forces and bending moments. Develop shear and
moment diagrams.

11. Course Outcomes 2
• Solve beam deflection problems using integration,
and superposition.
• Solve for the stresses in beams with combined
axial and transverse loads.
• Solve for stresses in general cases of combined
loading and check for yielding using simple yield
criteria.

12. Statics Review: External Loads
One body
acting on
another
Small contact area;
treat as a point
One body
acting on
another w/o
contact
Acting on
narrow area
FR is
resultant of
w(s) = area
under curve,
acts at
centroid
Begin Chapter 1:

13. External Loads:
• External loads can be Reaction Loads
or Applied Loads!
• Must solve for all unknown external
loads (reaction loads) so that internal
loads can be solved for!
• Internal loads produce stress, strain,
deformation – SofM concepts!

14. Support Types and Reactions (2D):

15. Support Types and Reactions (2D):

16. Pin connections
allow rotation.
Reactions at pins
are forces and
NOT MOMENTS.
Degrees of
Freedom

17. Static Equilibrium
• Vectors: SF = 0 SM = 0
• Coplanar (2D) force systems:
SFx = 0
SFy = 0
SMo = 0 Perpendicular
to the plane
containing the
forces
• Draw a FBD to account for
ALL loads acting on the body.

18. Example FBD:
Draw a FBD of member ABC, which is supported
by a smooth collar at A, roller at B, and link CD.

19. GROUP PROBLEM SOLVING (continued)
FBD

20. Example: Find the vertical reactions at A and B
for the shaft shown.

21. FBD
See Page 10, Procedure for Analysis for FBD hints.
A B
Ay By
225 N
(800 N/m)(0.150 m) = 120 N
Comment on dashed line around the distributed load.

22. Equilibrium
Equations


S




S
N18.75
N363.75
y
y
y
y
yA
A
N75.18A
N225N75.363N120Ay0Fy
B
m400.
)m500(.N225)m275(.N120
B
)m500(.N225)m275(.N120)B(m400.0M+
+

23. STATICS: You need to be
able to…
• Draw free-body diagrams,
• Know support types and their corresponding
reactions,
• Write and solve equilibrium equations so that
unknown forces can be solved for,
• Solve for appropriate internal loads by taking
cuts of inspection,
• Determine the centroid of an area,
• Determine the moment of inertia about an
axis through the centroid of an area.

24. Internal Reactions
• Internal reactions are
necessary to hold body
together under loading.
• Method of sections -
make a cut through
body to find internal
reactions at the point of
the cut.

25. FBD After Cut
• Separate the two parts
and draw a FBD of
either side
• Use equations of
equilibrium to relate the
external loading to the
internal reactions.

26. Resultant Force and Moment
• Point O is taken at the
centroid of the section.
• If the member (body) is
long and slender, like a
rod or beam, the
section is generally
taken perpendicular to
the longitudinal axis.
• Section is called the
cross section.

27. Components of Resultant
• Components are
found
perpendicular &
parallel to the
section plane.
• Internal reactions
are used to
determine stresses.

28. Coplanar Force System
VDifferent than
Fig. 1-3(b)
Start with internal system
of forces as shown below
to get proper signs for V,
N and M.

29. Types of loading

30. Summary of Typical Strength of Material Problem:
1. Calculate unknown reaction forces first.
2. Calculate internal forces at point of interest by cutting
member if necessary.
3. Calculate area properties (inertia, centroid, area, etc.).
4. Calculate stress!!
Examples of 1 and 2 follow

35. EXAMPLE
1. Check if there are any zero-force members.
2. First analyze pin D and then pin A
3. Note that member BD is zero-force member. FBD = 0
4. Why, for this problem, do you not have to find the external
reactions before solving the problem?
Given: Loads as shown on the truss
Find: The forces in each member
of the truss.
Plan:

36. EXAMPLE (continued)
+   FX = – 450 + FCD cos 45° – FAD cos 45° = 0
+   FY = – FCD sin 45° – FAD sin 45° = 0
FCD = 318 lb (Tension) or (T)
and FAD = – 318 lb (Compression) or (C)
45 º
FCD
D 450 lb
FAD
FBD of pin D
45 º

37. EXAMPLE (continued)
+   FX = FAB + (– 318) cos 45° = 0; FAB = 225 lb (T)
Could you have analyzed Joint C instead of A?
45 º
FAB
A
FBD of pin A
FAD
AY
Analyzing pin A:

38. Example 4: The 500 kg engine is suspended from the boom crane as
shown. Determine resultant internal loadings acting on the cross
section of the boom at point E.