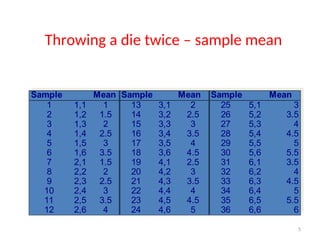
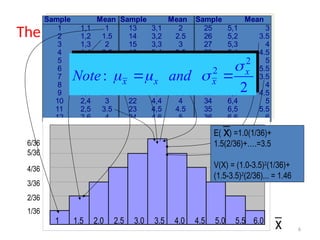
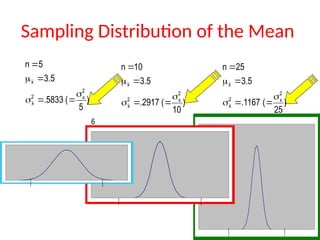
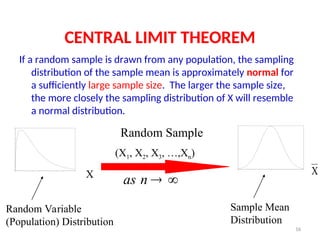
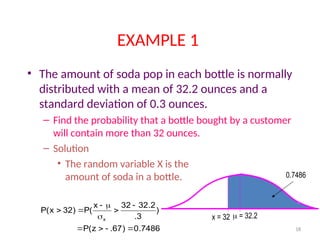
The document explains the concept of sampling distributions, emphasizing their role in estimating population parameters using sample statistics. It discusses the sampling distribution of the mean, central limit theorem, and the conditions under which sample means approximate a normal distribution. Additionally, it covers properties of sampling distributions regarding sample variances and proportions, along with illustrative examples.

1. SAMPLING DISTRIBUTION

2. 2
Introduction
• In real life calculating parameters of populations is
usually impossible because populations are very
large.
• Rather than investigating the whole population,
we take a sample, calculate a statistic related to
the parameter of interest, and make an inference.
• The sampling distribution of the statistic is the
tool that tells us how close is the statistic to the
parameter.

3. 3
Sampling Distribution of the Mean
• An example
– A die is thrown infinitely many times. Let X
represent the number of spots showing on any
throw.
– The probability distribution of X is
x 1 2 3 4 5 6
p(x) 1/6 1/6 1/6 1/6 1/6 1/6
E(X) = 1(1/6) +
2(1/6) + 3(1/6)+
………………….= 3.5
V(X) = (1-3.5)2
(1/6) +
(2-3.5)2
(1/6) +

4. 4
• Suppose we want to estimate  from
the mean of a sample of size n = 2.
• What is the distribution of ?
X
Throwing a die twice – sample mean
X

5. 5
Sample Mean Sample Mean Sample Mean
1 1,1 1 13 3,1 2 25 5,1 3
2 1,2 1.5 14 3,2 2.5 26 5,2 3.5
3 1,3 2 15 3,3 3 27 5,3 4
4 1,4 2.5 16 3,4 3.5 28 5,4 4.5
5 1,5 3 17 3,5 4 29 5,5 5
6 1,6 3.5 18 3,6 4.5 30 5,6 5.5
7 2,1 1.5 19 4,1 2.5 31 6,1 3.5
8 2,2 2 20 4,2 3 32 6,2 4
9 2,3 2.5 21 4,3 3.5 33 6,3 4.5
10 2,4 3 22 4,4 4 34 6,4 5
11 2,5 3.5 23 4,5 4.5 35 6,5 5.5
12 2,6 4 24 4,6 5 36 6,6 6
Throwing a die twice – sample mean

6. 6
X
The distribution of when n = 2
Sample Mean Sample Mean Sample Mean
1 1,1 1 13 3,1 2 25 5,1 3
2 1,2 1.5 14 3,2 2.5 26 5,2 3.5
3 1,3 2 15 3,3 3 27 5,3 4
4 1,4 2.5 16 3,4 3.5 28 5,4 4.5
5 1,5 3 17 3,5 4 29 5,5 5
6 1,6 3.5 18 3,6 4.5 30 5,6 5.5
7 2,1 1.5 19 4,1 2.5 31 6,1 3.5
8 2,2 2 20 4,2 3 32 6,2 4
9 2,3 2.5 21 4,3 3.5 33 6,3 4.5
10 2,4 3 22 4,4 4 34 6,4 5
11 2,5 3.5 23 4,5 4.5 35 6,5 5.5
12 2,6 4 24 4,6 5 36 6,6 6
1 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0
6/36
5/36
4/36
3/36
2/36
1/36
x
E( ) =1.0(1/36)+
1.5(2/36)+….=3.5
V(X) = (1.0-3.5)2
(1/36)+
(1.5-3.5)2
(2/36)... = 1.46
x
2
2
:
2
x
x x x
Note and

  
 

7. 7
6
)
5
(
5833
.
5
.
3
5
n
2
x
2
x
x







)
10
(
2917
.
5
.
3
10
n
2
x
2
x
x







)
25
(
1167
.
5
.
3
25
n
2
x
2
x
x







Sampling Distribution of the Mean

8. 8
Sampling Distribution of the Mean
)
5
(
5833
.
5
.
3
5
n
2
x
2
x
x







)
10
(
2917
.
5
.
3
10
n
2
x
2
x
x







)
25
(
1167
.
5
.
3
25
n
2
x
2
x
x







Notice that is smaller than .
The larger the sample size the
smaller . Therefore, tends
to fall closer to , as the sample
size increases.
2
x

x
2
x

Notice that is smaller than x.
The larger the sample size the
smaller . Therefore, tends
to fall closer to , as the sample
size increases.
2
x

x
2
x

2

9. 9
SAMPLING DISTRIBUTION
• Let X1, X2,…,Xn be a r.s. of size n from a
population and let T(x1,x2,…,xn) be a real (or
vector-valued) function whose domain includes
the sample space of (X1, X2,…,Xn). Then, the
r.v. or a random vector Y=T(X1, X2,…,Xn) is
called a statistic. The probability distribution of
a statistic Y is called the sampling distribution
of Y.

10. 10
SAMPLING DISTRIBUTION
• The sample mean is the arithmetic average of
the values in a r.s.
1 2
1
1 n
n
i
i
X X X
X X
n n 
  
  

• The sample variance is the statistic defined by
 
2
2
1
1
1
n
i
i
S X X
n 
 


• The sample standard deviation is the statistic
defined by S.

11. 11
SAMPLING FROM THE NORMAL
DISTRIBUTION
Properties of the Sample Mean and Sample
Variance
• Let X1, X2,…,Xn be a r.s. of size n from a
N(,2
) distribution. Then,
2
) and are independent rvs.
a X S
 
2
) ~ , /
b X N n
 
  2
2
1
2
1
) ~ n
n S
c 
 


12. 12
SAMPLING FROM THE NORMAL
DISTRIBUTION
• Let X1, X2,…,Xn be a r.s. of size n from a
N(,2
) distribution. Then,
 
~ 0,1
/
X
N
n



•Most of the time  is unknown, so we use:
.
/
X
S n



13. 13
SAMPLING FROM THE NORMAL
DISTRIBUTION
In statistical inference, Student’s t
distribution is very important.

14. 14
SAMPLING FROM THE NORMAL
DISTRIBUTION
• Let X1, X2,…,Xn be a r.s. of size n from a
N(X,X
2
) distribution and let Y1,Y2,…,Ym
be a r.s. of size m from an independent
N(Y,Y
2
).
• If we are interested in comparing the
variability of the populations, one
quantity of interest would be the ratio
2 2 2 2
/ /
X Y X Y
S S
  

15. 15
SAMPLING FROM THE NORMAL
DISTRIBUTION
• The F distribution allows us to compare these
quantities by giving the distribution of
2 2 2 2
1, 1
2 2 2 2
/ /
~
/ /
X Y X X
n m
X Y Y Y
S S S
F
S

    

• If X~Fp,q, then 1/X~Fq,p.
• If X~tq, then X2
~F1,q.

16. 16
CENTRAL LIMIT THEOREM
If a random sample is drawn from any population, the sampling
distribution of the sample mean is approximately normal for
a sufficiently large sample size. The larger the sample size,
the more closely the sampling distribution of X will resemble
a normal distribution.
Random Sample
(X1, X2, X3, …,Xn)
Sample Mean
Distribution
X
X
Random Variable
(Population) Distribution
as n  

17. 17
Sampling Distribution of the Sample
Mean
If X is normal, is normal. If X is non-normal,
is approximately normally distributed for
sample size greater than or equal to 30.
X
 

2
2
or
X X
n n
 
 
 
X
X
2 X
X ~ N( , / n ) Z ~ N(0,1)
/ n
 
   


18. 18
• The amount of soda pop in each bottle is normally
distributed with a mean of 32.2 ounces and a
standard deviation of 0.3 ounces.
– Find the probability that a bottle bought by a customer
will contain more than 32 ounces.
– Solution
• The random variable X is the
amount of soda in a bottle.
 = 32.2
0.7486
x = 32
7486
.
0
)
67
.
z
(
P
)
3
.
2
.
32
32
x
(
P
)
32
x
(
P
x











EXAMPLE 1

19. 19
 = 32.2
0.7486
x = 32
• Find the probability that a carton of four bottles will have
a mean of more than 32 ounces of soda per bottle.
• Solution
– Define the random variable as the mean amount of soda per
bottle.
9082
.
0
)
33
.
1
z
(
P
)
4
3
.
2
.
32
32
x
(
P
)
32
x
(
P
x











32
x 
0.9082
2
.
32
x 

EXAMPLE 1 (contd.)

20. 20
The estimate of p =
The estimate of p =
• The parameter of interest for nominal data is
the proportion of times a particular outcome
(success) occurs.
• To estimate the population proportion ‘p’ we
use the sample proportion.
Sampling Distribution of
a Proportion
p
p
^
^ =
=
X
X
n
n
The number
of successes

21. 21
• Since X is binomial, probabilities about can
be calculated from the binomial distribution.
• Yet, for inference about we prefer to use
normal approximation to the binomial
whenever it approximation is appropriate.
p
p
^
^
Sampling Distribution of
a Proportion
p
p
^
^

22. 22
Approximate Sampling Distribution of a
Sample Proportion
• From the laws of expected value and variance, it can be
shown that E( ) = p and V( )=p(1-p)/n
• If both np ≥ 5 and n(1-p) ≥ 5, then
• Z is approximately standard normally distributed.
ˆ
(1 )
p p
z
p p
n



p̂ p̂

23. 23
EXAMPLE
– A state representative received 52% of the
votes in the last election.
– One year later the representative wanted to
study his popularity.
– If his popularity has not changed, what is the
probability that more than half of a sample of
300 voters would vote for him?

24. 24
EXAMPLE (contd.)
Solution
• The number of respondents who prefer the representative is
binomial with n = 300 and p = .52. Thus, np = 300(.52) = 156 and
n(1-p) = 300(1-.52) = 144 (both greater than 5)
7549
.
300
)
52
.
1
)(
52
(.
52
.
50
.
)
1
(
ˆ
)
50
.
ˆ
( 















n
p
p
p
p
P
p
P