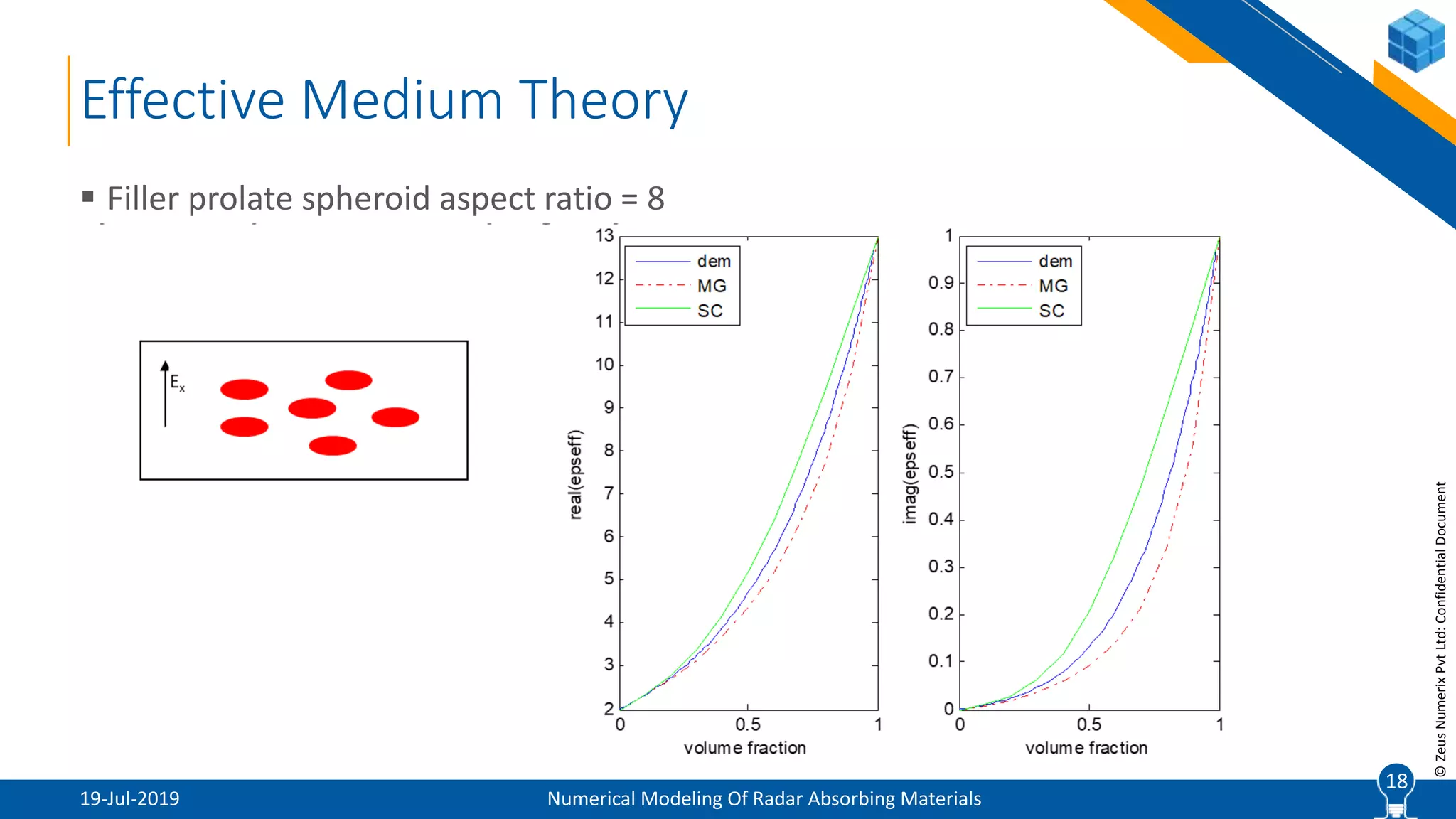
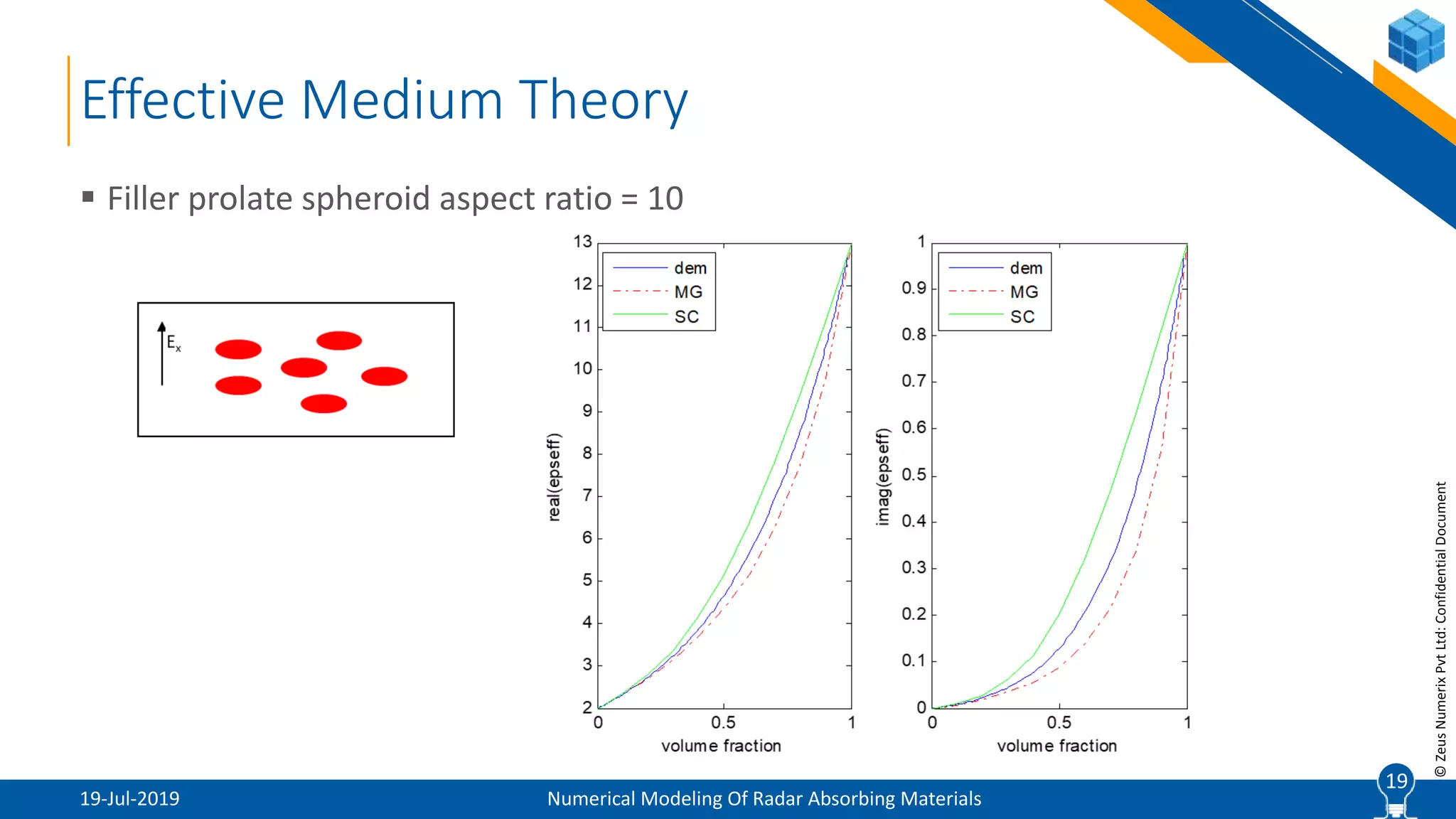
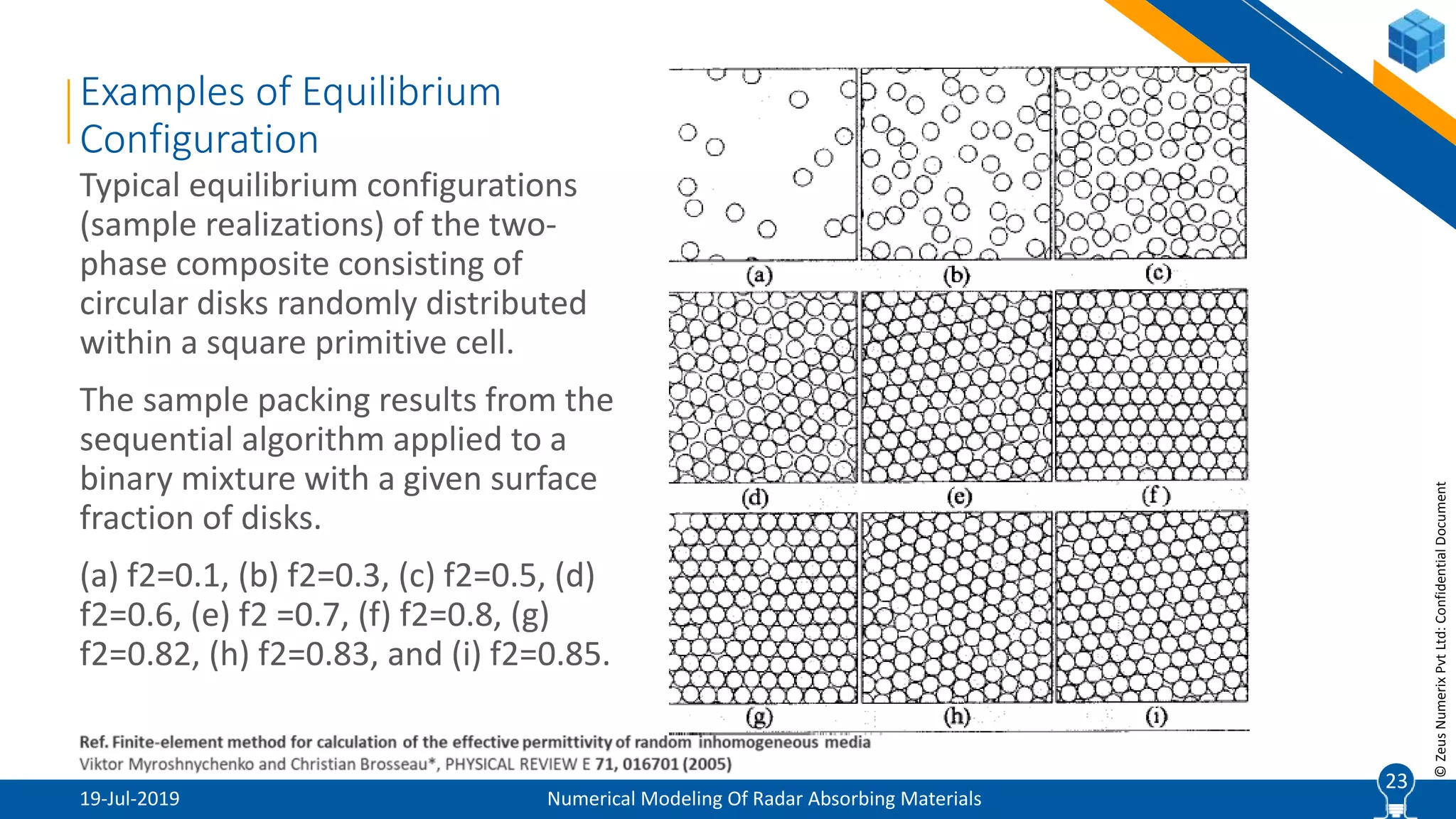
The document provides a comprehensive overview of numerical modeling of radar absorbing materials (RAM), detailing their design, types, and effective medium theories. It discusses the importance of composite materials for radar signature reduction, different classification methods of RAM, and advanced techniques for their optimization. Additionally, it explains computational approaches for calculating effective properties and addresses the challenges in simulating random microstructures within these materials.













![24
©ZeusNumerixPvtLtd:ConfidentialDocument
Assume cubic shape of inclusion
[Xi, Yj, Zk] coordinates / sites
i = 1,..,Nx
Nx = no. of unit cells along X =
Length of X axis / unit cell dimension along X
axis
j = 1,..,Ny
k = 1,..,Nz
Random nos. along X = ( 3√f * Nx )
f = volume fraction of inclusion
Run random no. generation engine (1+ 3√f *
Ny * 3√f * Nz) times to get 3D profile of
composite
19-Jul-2019 Numerical Modeling Of Radar Absorbing Materials
24
Alternate Method](https://image.slidesharecdn.com/10numerical-modeling-radar-absorbing-materials-201203130938/75/CEM-Workshop-Lectures-10-11-Numerical-Modeling-of-Radar-Absorbing-Materials-24-2048.jpg)