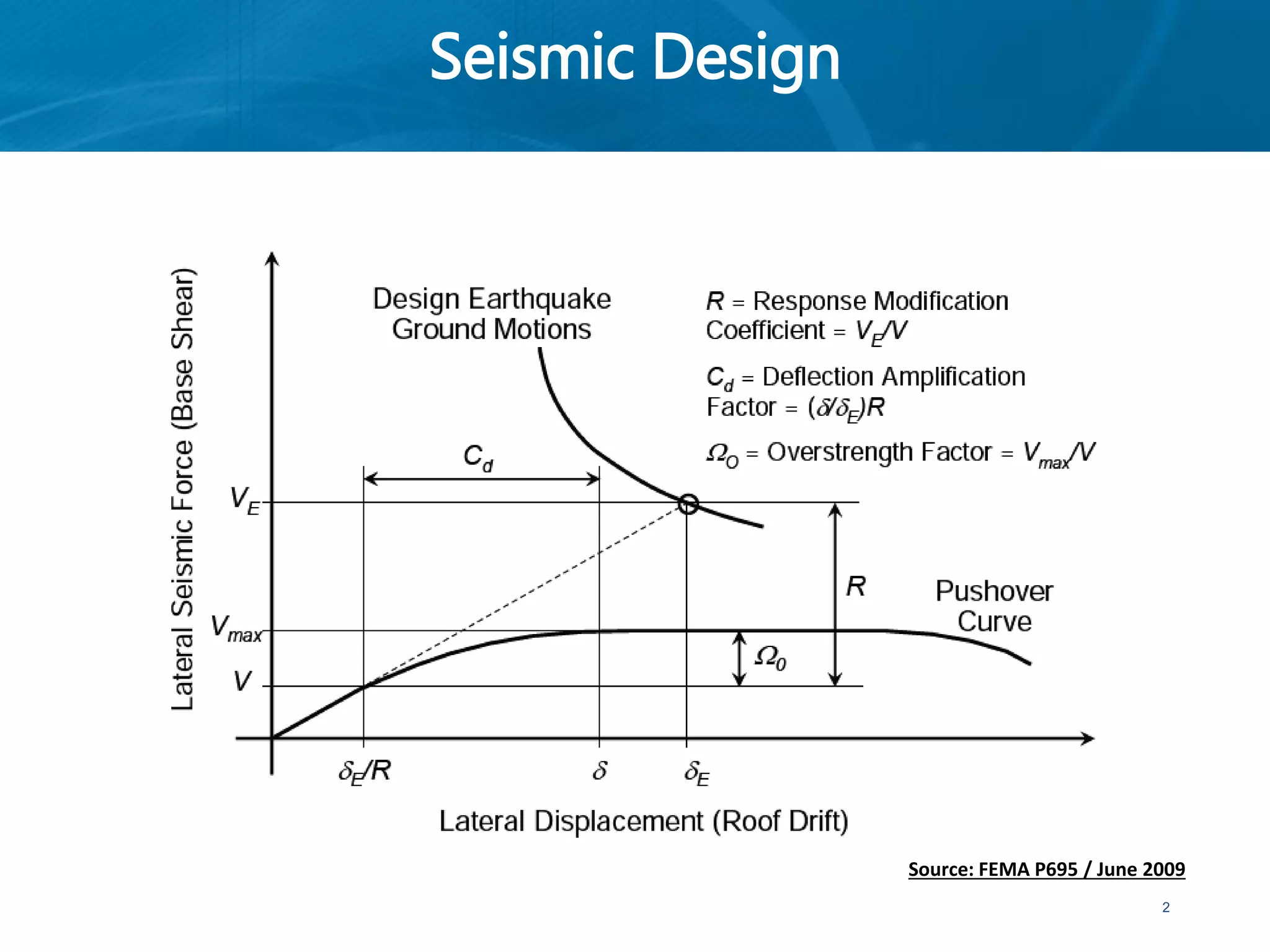
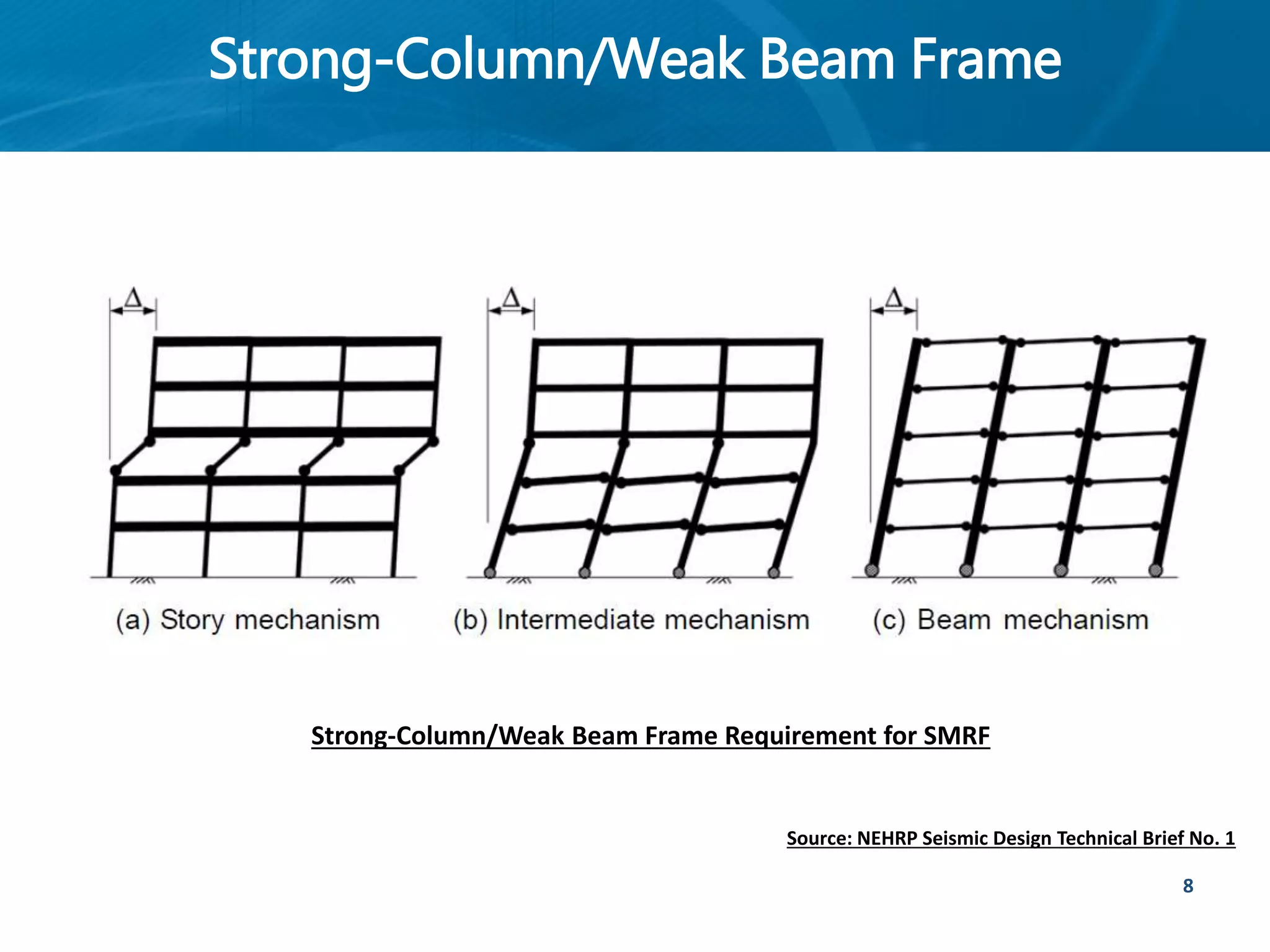
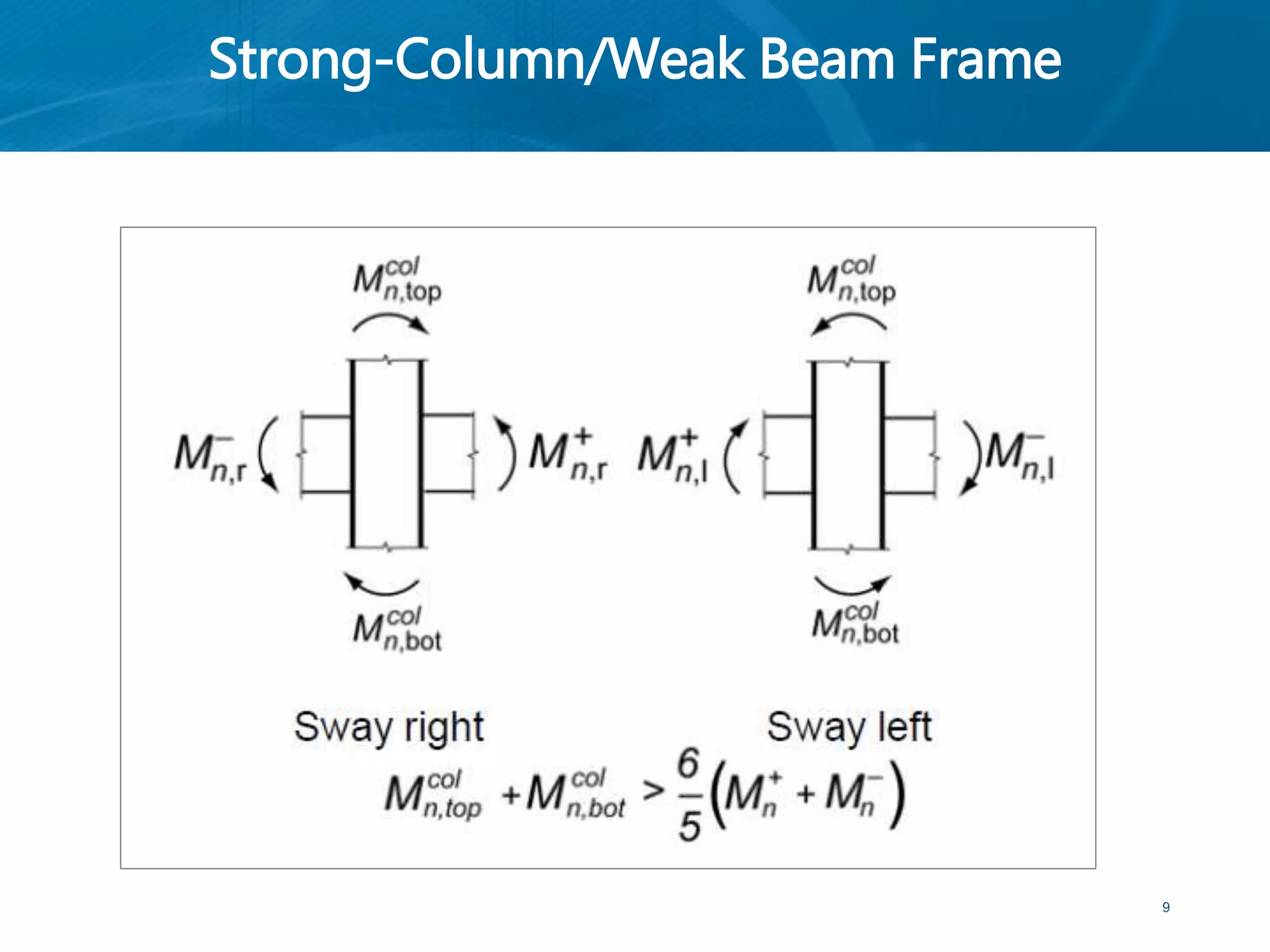
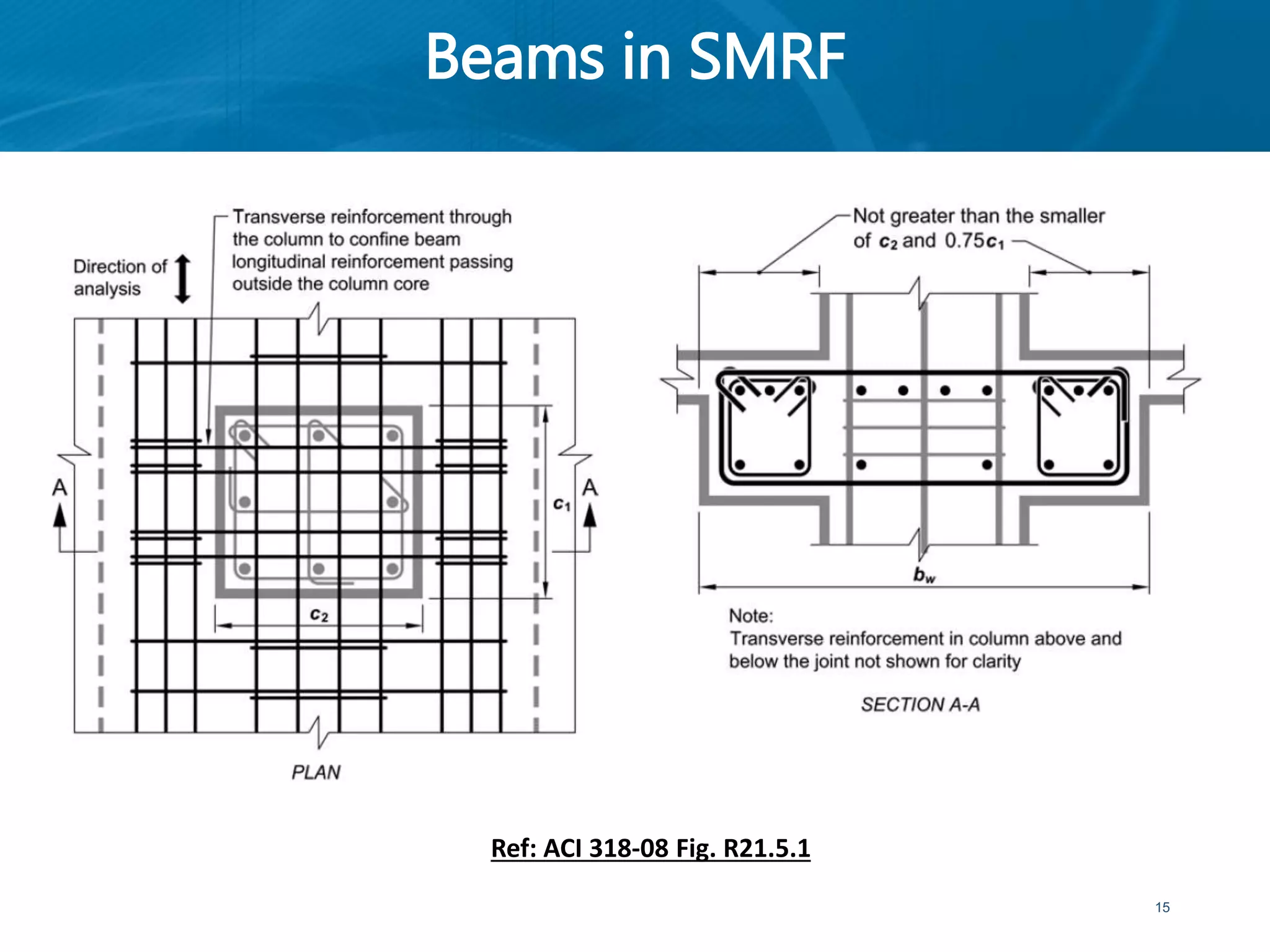
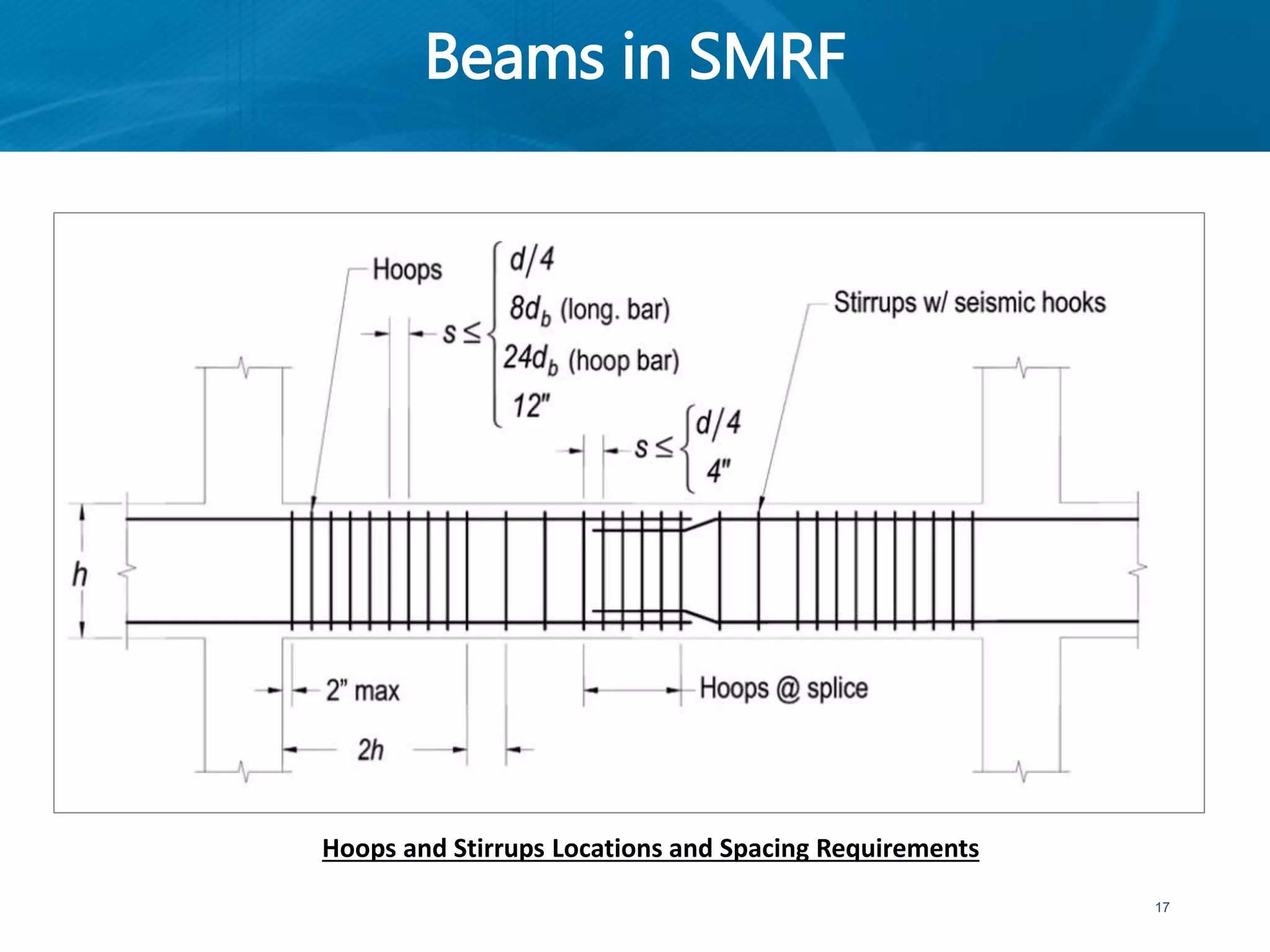
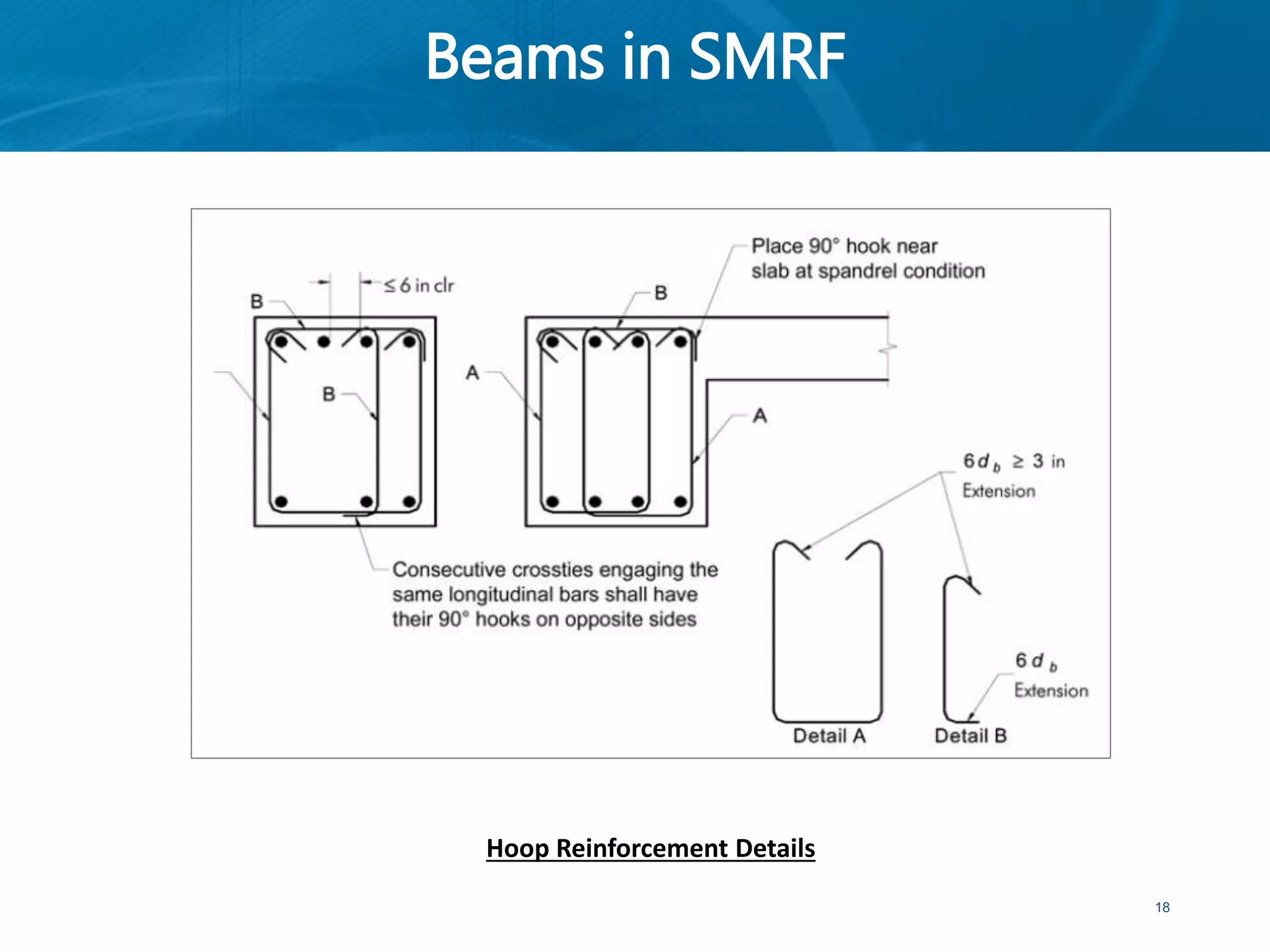
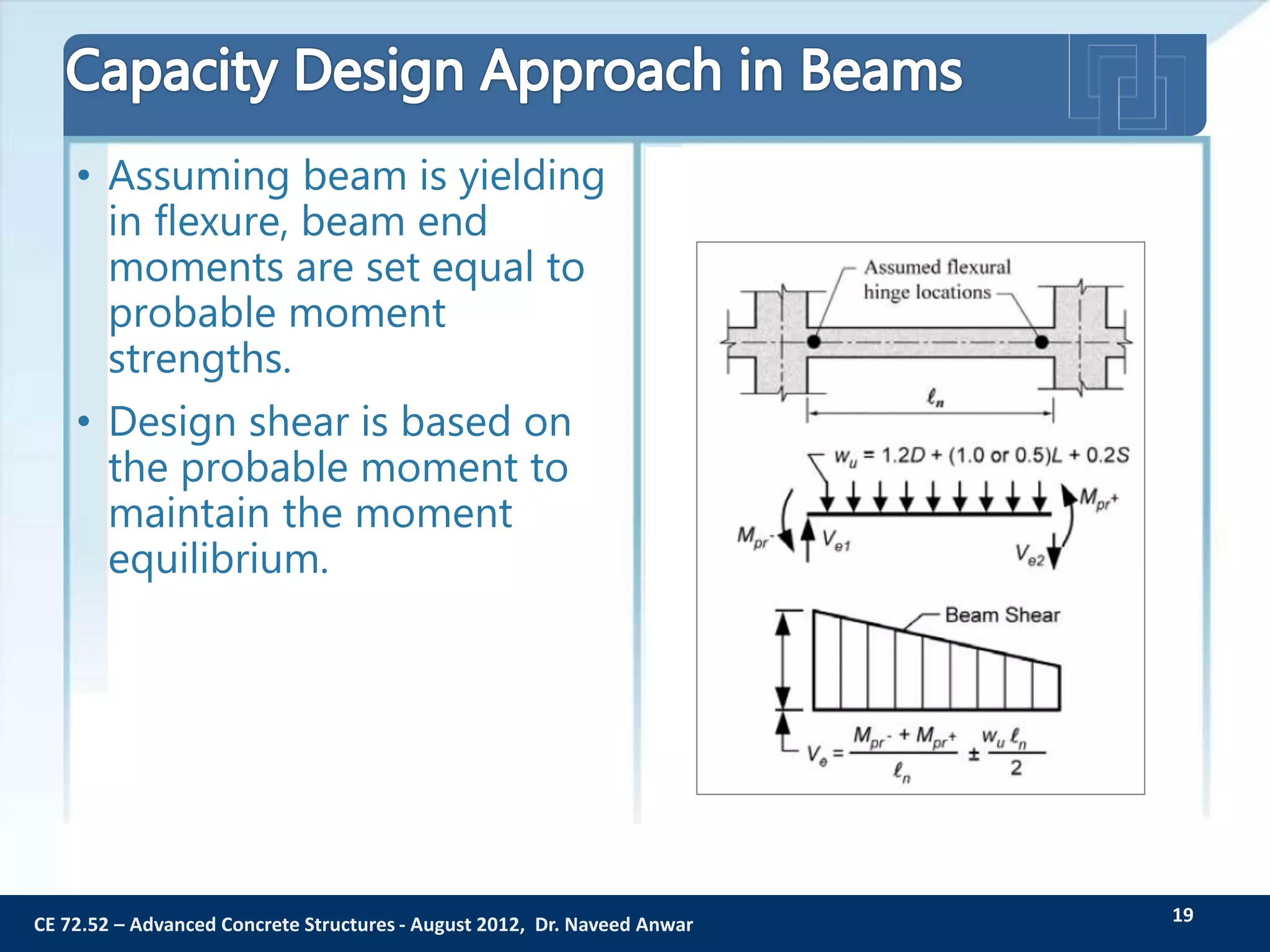
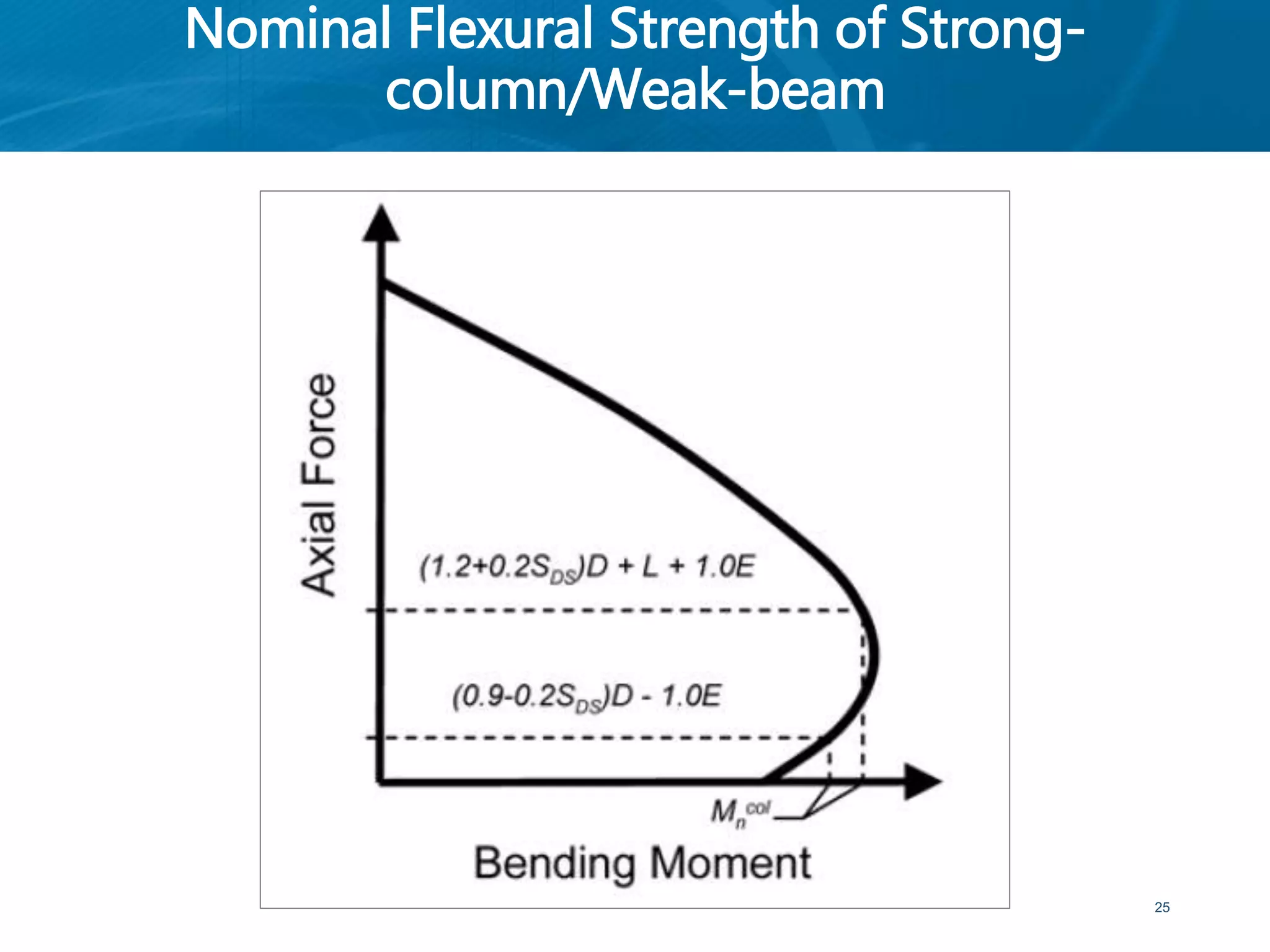
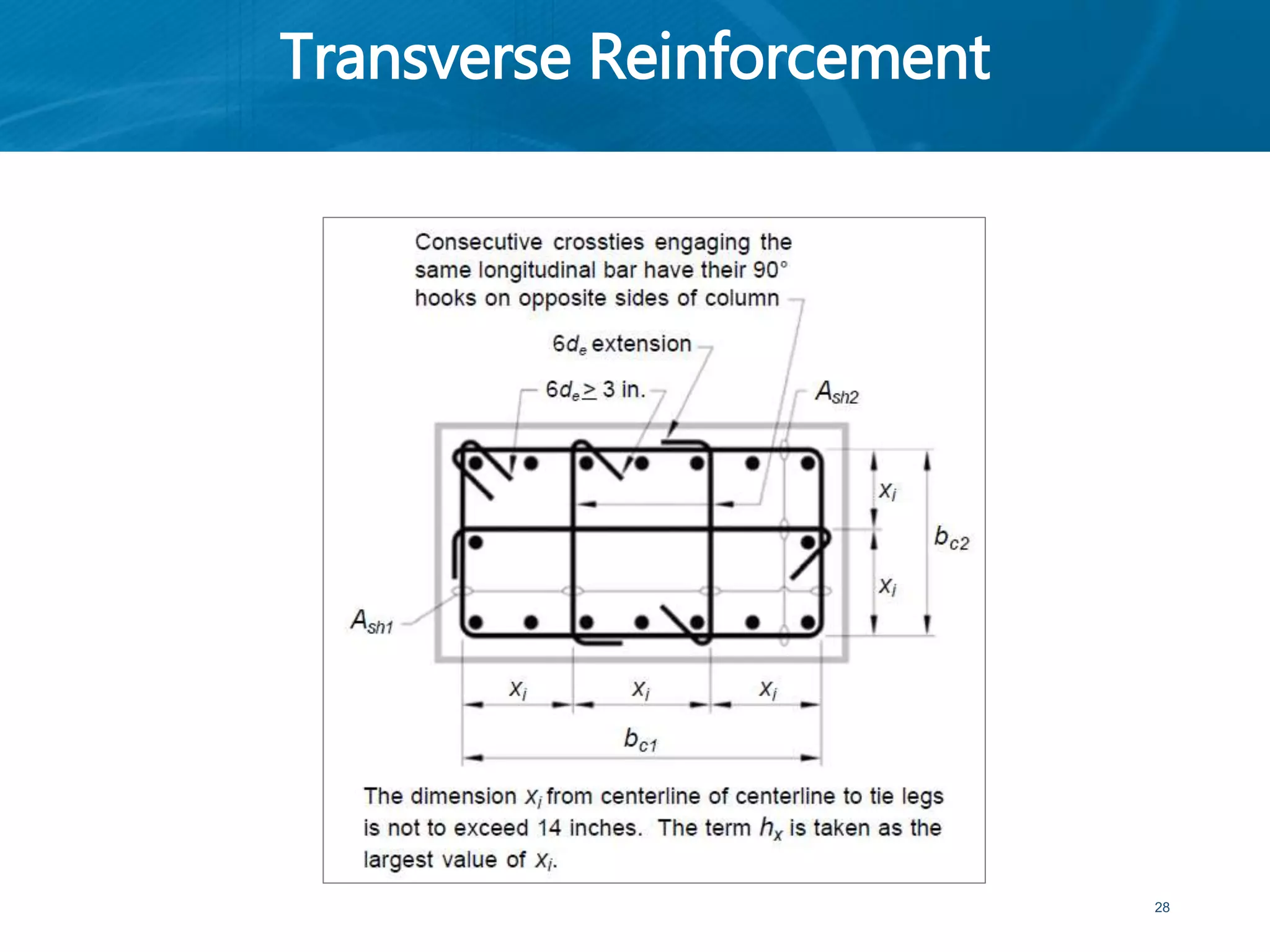
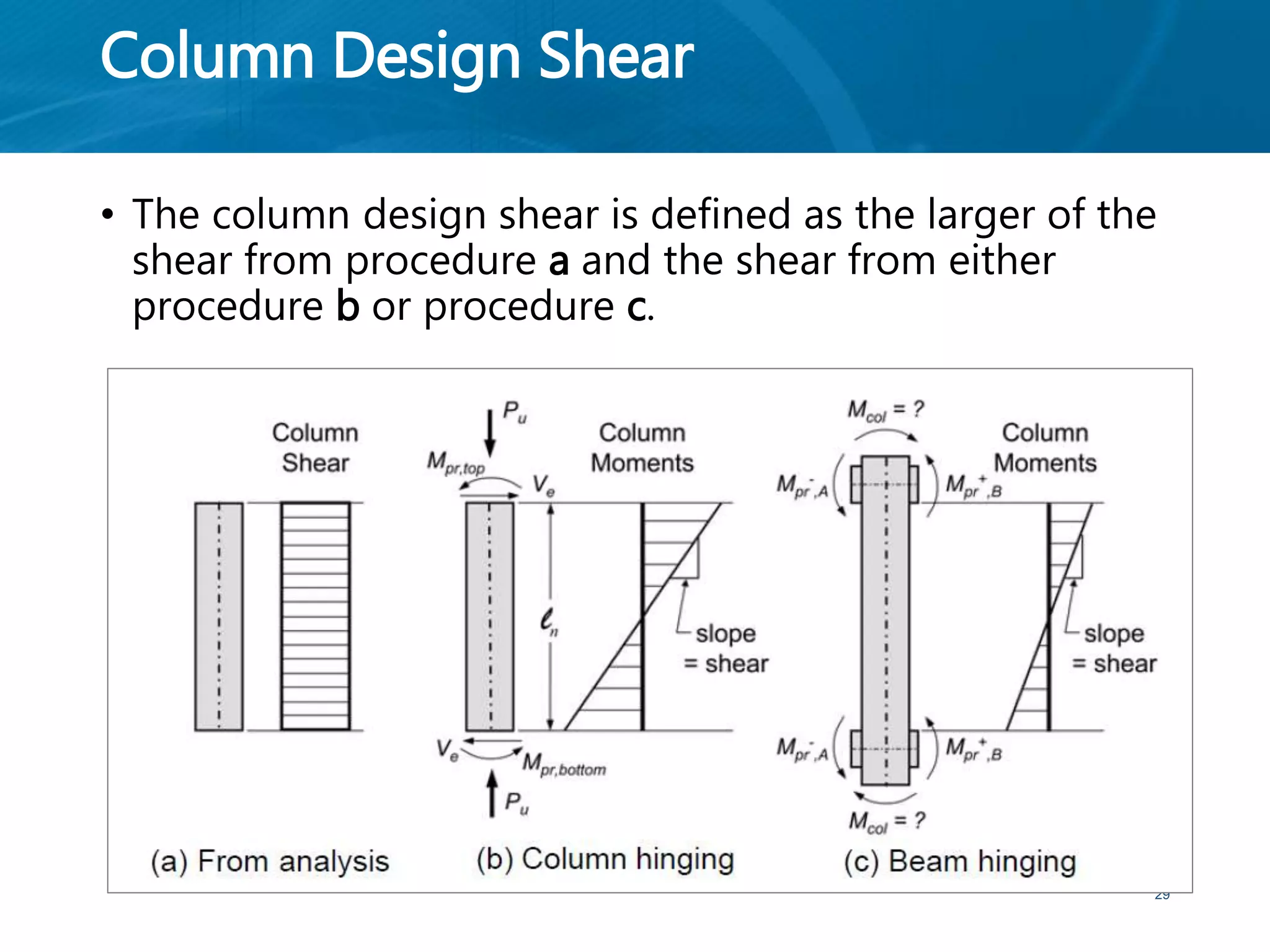
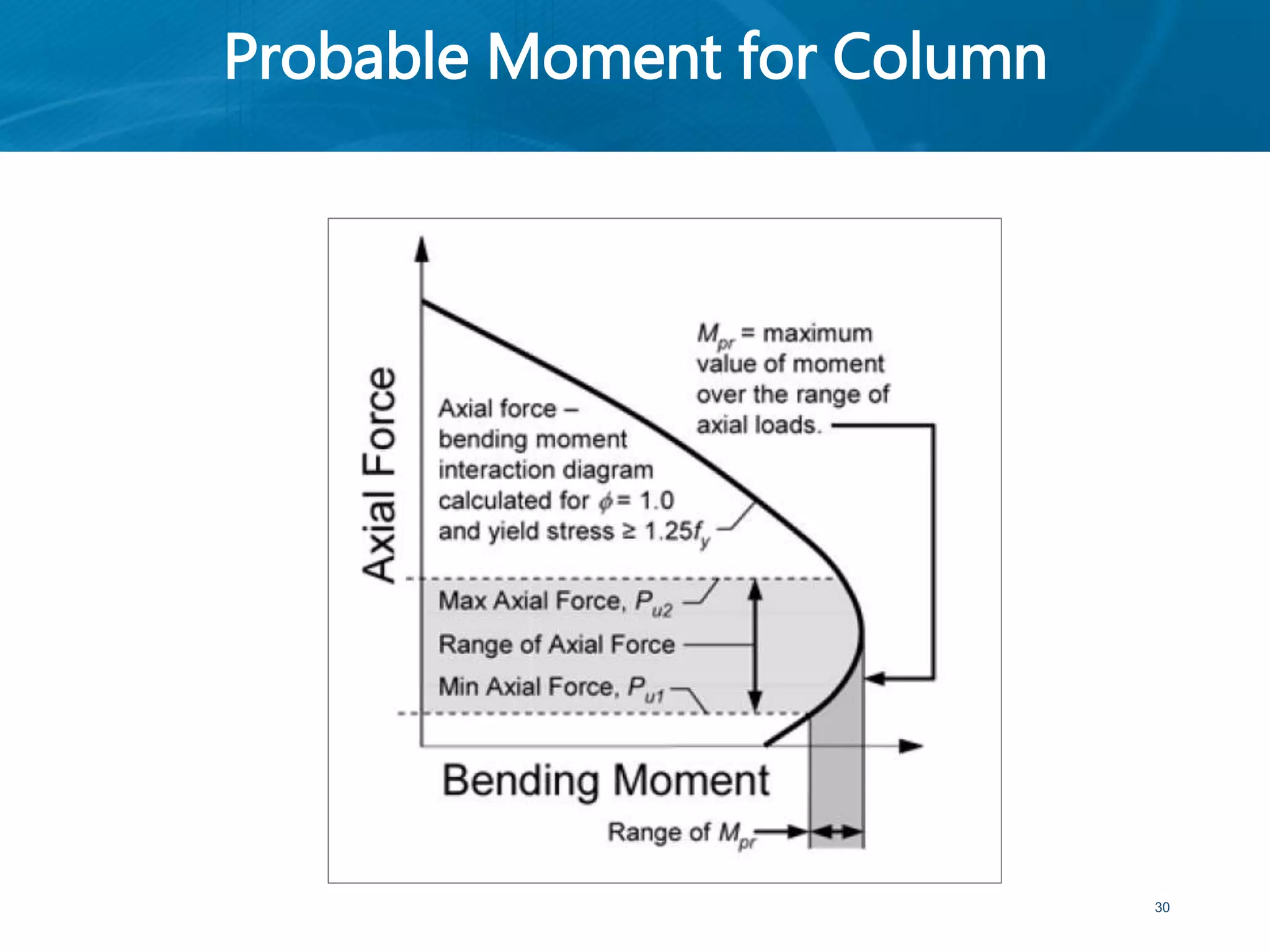
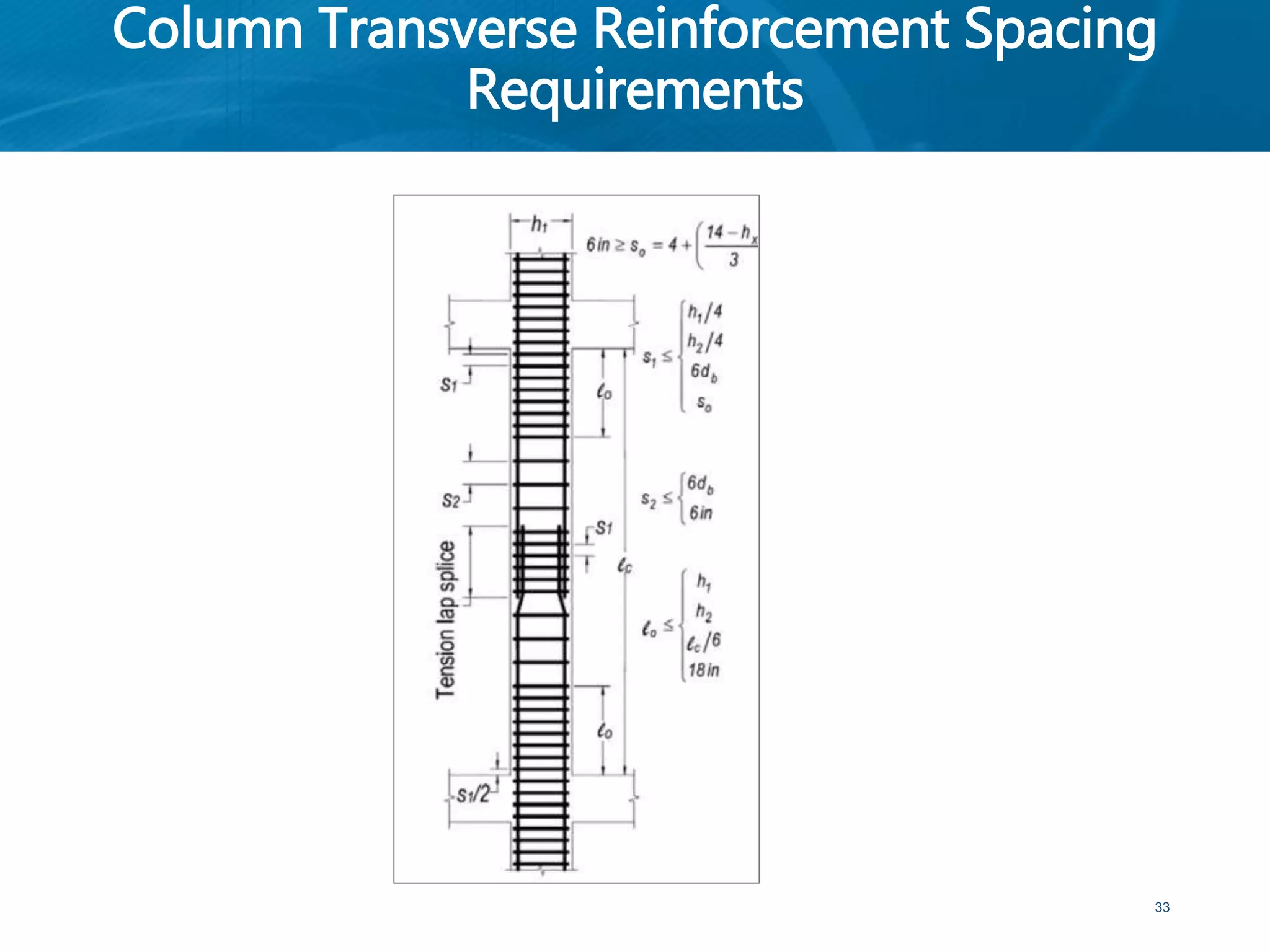
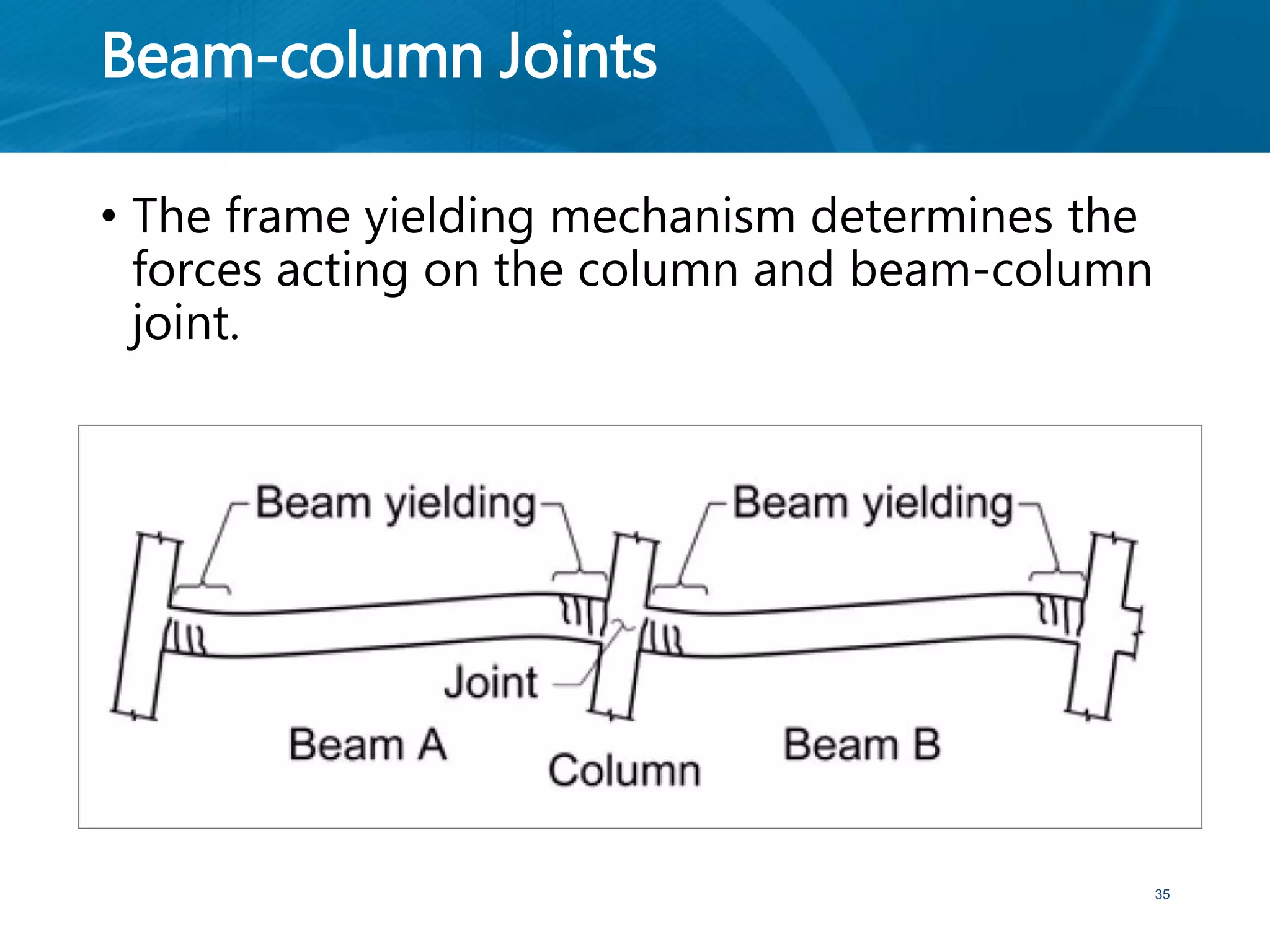
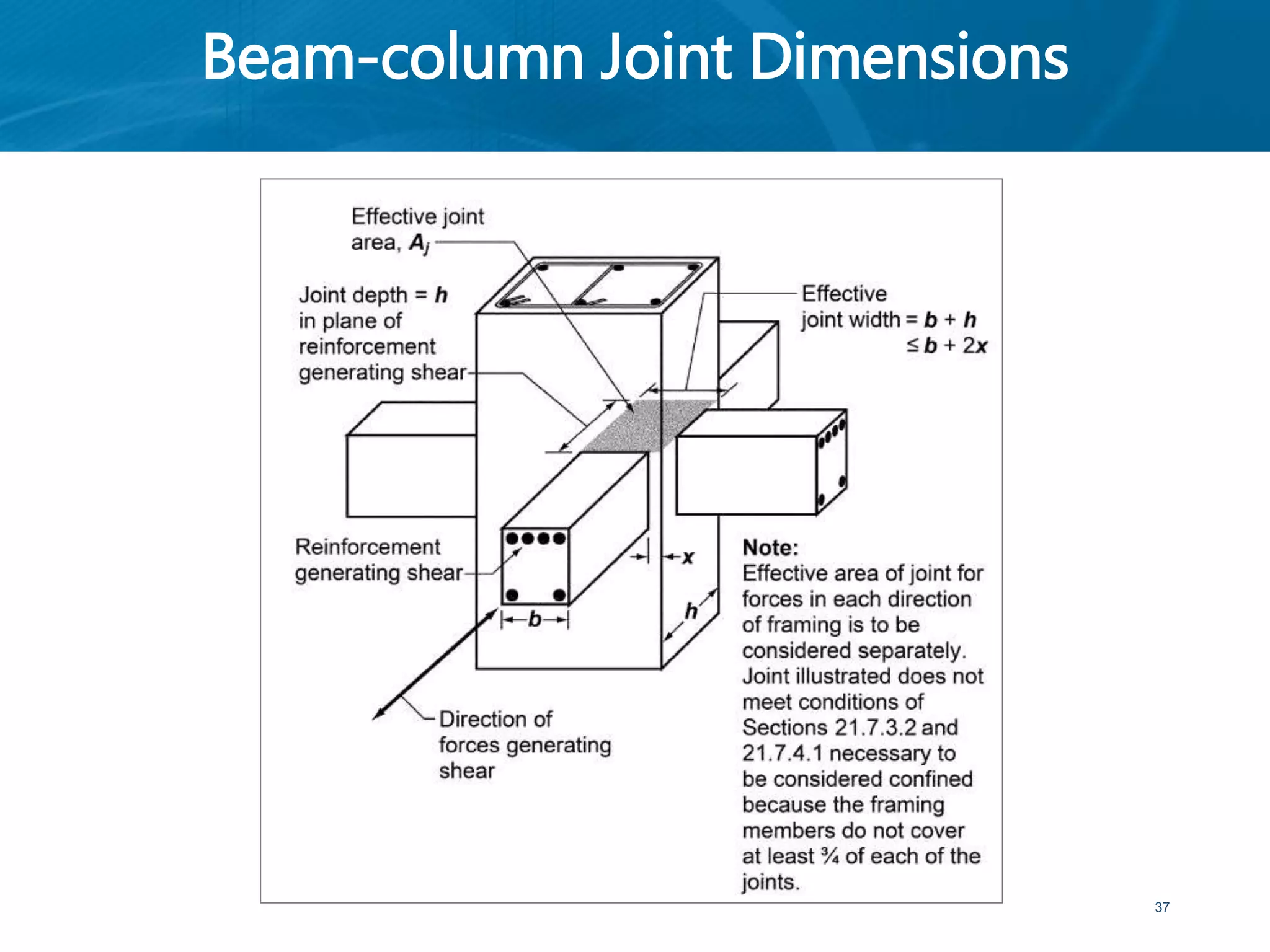
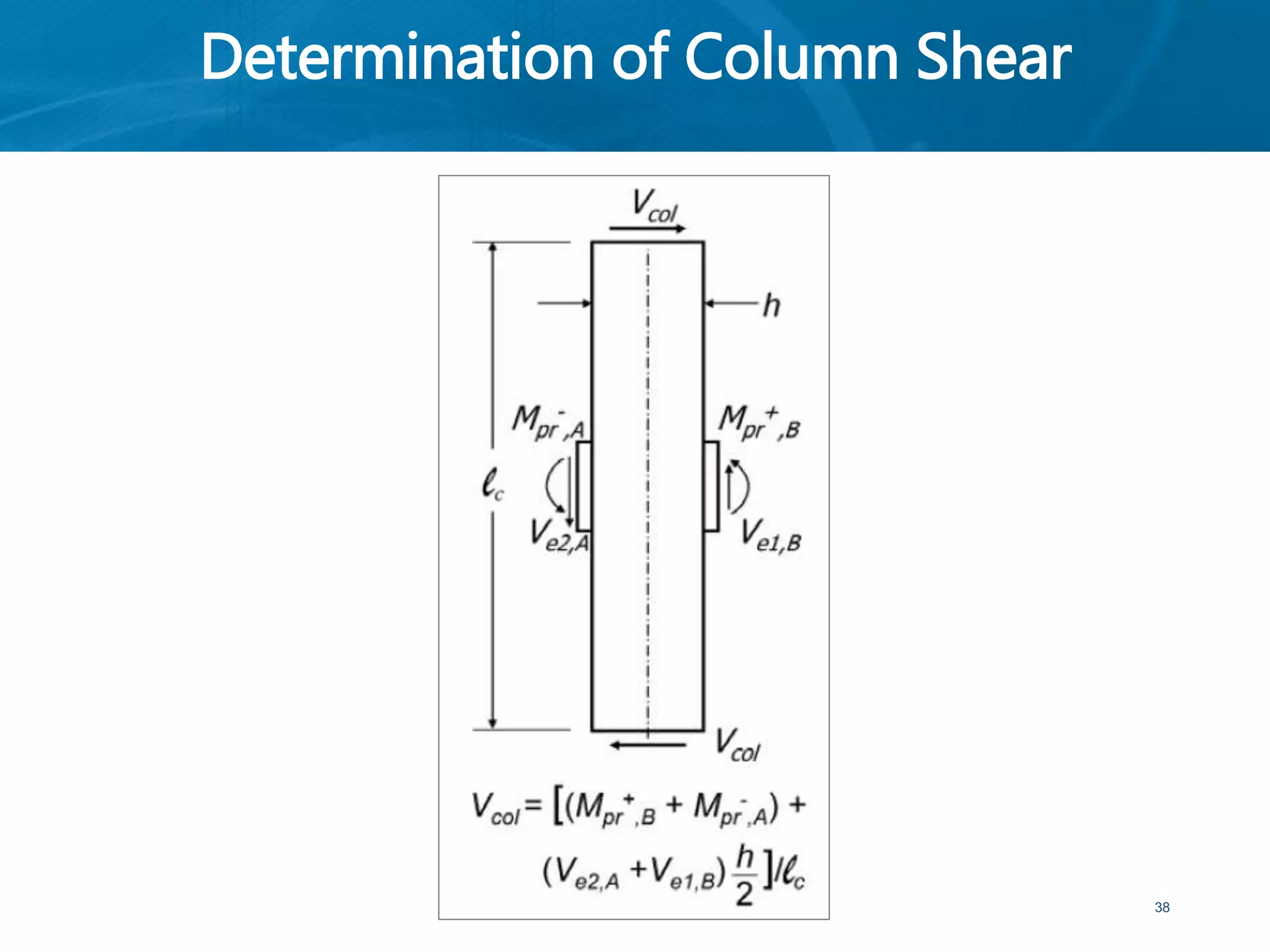
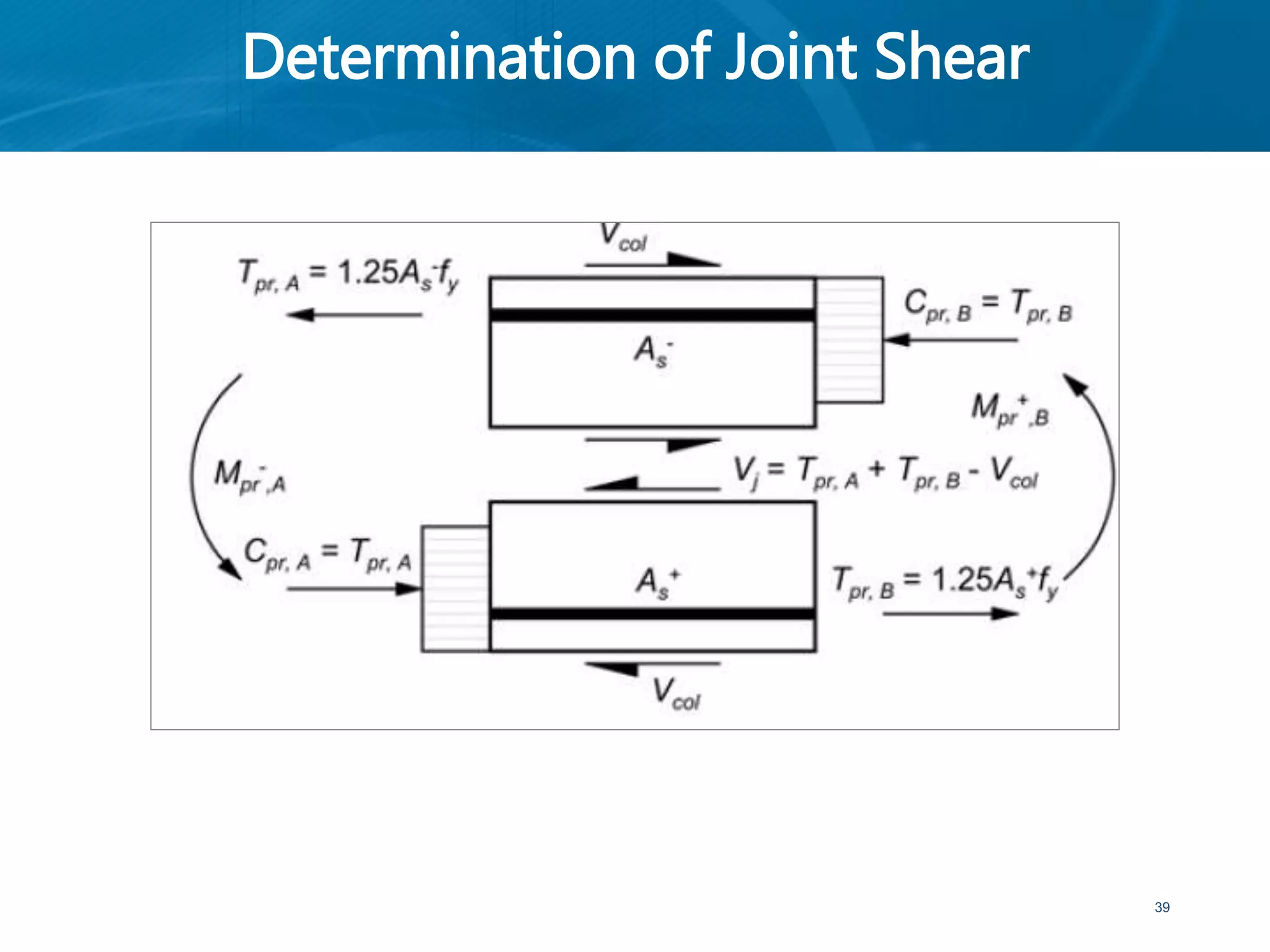
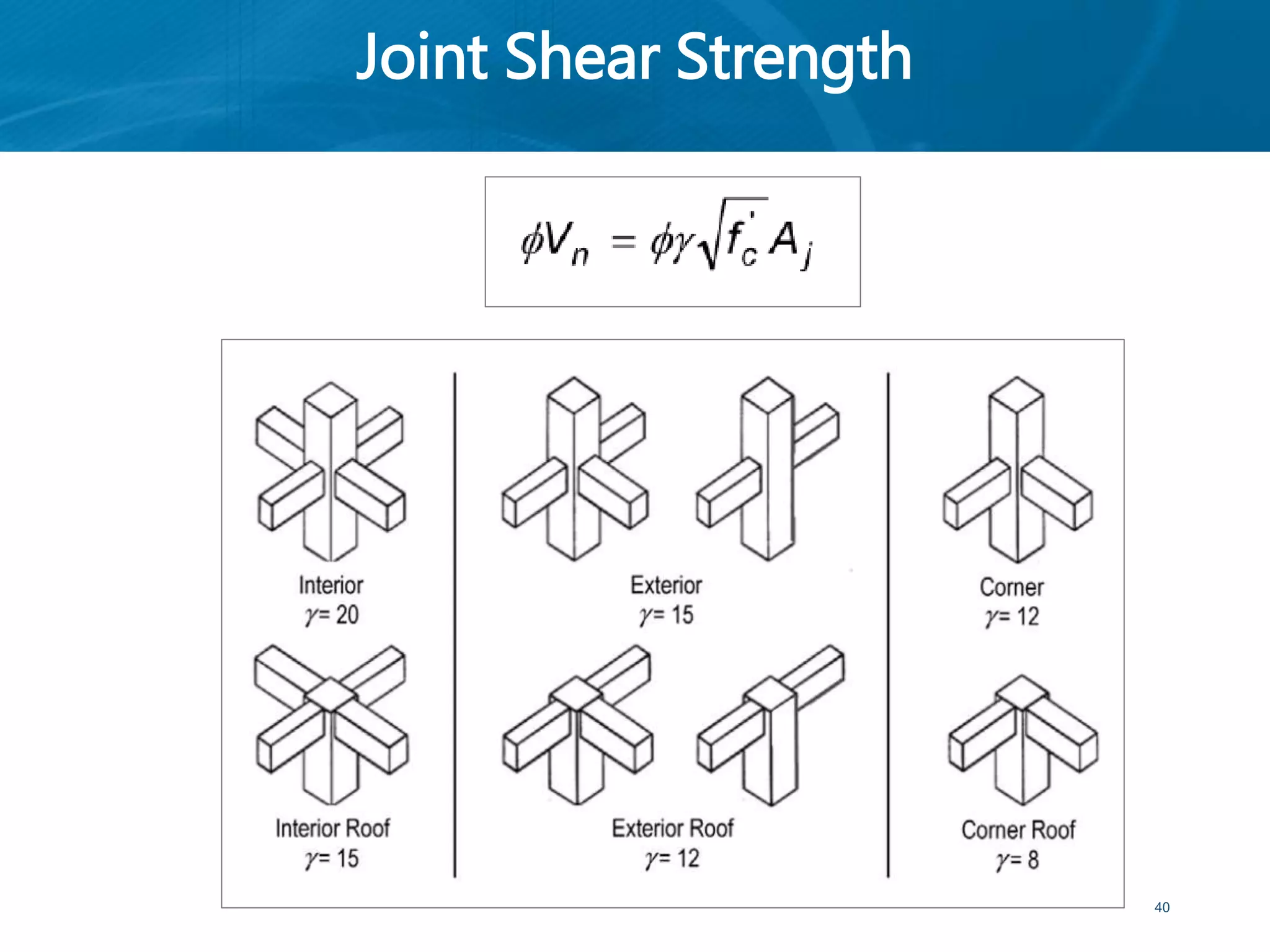
This document provides an overview of member behavior for beams and columns in seismic design. It discusses the types of moment resisting frames and the principles for designing special moment resisting frames, including strong-column/weak-beam design, avoiding shear failure, and providing ductile details. Beam and column design considerations are covered, such as dimensions, reinforcement, and shear capacity. Beam-column joint design is also summarized, including dimensions, shear determination, and strength.

1. 1
CE 72.52 Advanced Concrete
Lecture 4a:
Member
Behavior
(Beams and Columns)
Naveed Anwar
Executive Director, AIT Consulting
Director, ACECOMS
Affiliate Faculty, Structural Engineering, AIT
August - 2015

2. Seismic Design
2
Source: FEMA P695 / June 2009

3. Moment Resisting Frame
• Ordinary moment resisting frame (OMRF)
• Intermediate moment resisting frame (IMRF)
• Special moment resisting frame (SMRF)
3

4. Special Moment Resisting
Frame
4

5. Principles for Design of SMRF
• Proportioning and detailing requirements are
intended to ensure that inelastic response is
ductile.
• Three main goals
1) To achieve a strong-column/weak-beam design
that spreads inelastic response over several stories
2) To avoid shear failure
3) To provide details that enable ductile flexural
response in yielding regions
5

6. Design a Strong-column / Weak-beam
Frame
• If the building has weak columns, drift tends to
concentrate in one or a few stories, and may
exceed the drift capacity of the columns. If
columns provide a stiff and strong spine over the
building height, drift will be more uniformly
distributed and localized damage will be reduced.
• Additionally, it is important to recognize that the
columns in a given story support the weight of the
entire building above those columns, whereas the
beams only support the gravity loads of the floor
of which they form a part; therefore, failure of a
column is of greater consequence than failure of a
beam.
6

7. Design a Strong-column / Weak-beam
Frame
• ACI 318 adopts the strong-column/weak-beam
principle by requiring that the sum of column
strengths exceed the sum of beam strengths at
each beam-column connection of a special
moment frame. Studies have shown that the full
structural mechanism can only be achieved if the
column-to-beam strength ratio is relatively large
(on the order of four).
• As this is impractical in most cases, a lower
strength ratio of 1.2 is adopted by ACI 318. Some
column yielding associated with an intermediate
mechanism is to be expected, and columns must
be detailed accordingly.
7

8. Strong-Column/Weak Beam Frame
8
Strong-Column/Weak Beam Frame Requirement for SMRF
Source: NEHRP Seismic Design Technical Brief No. 1

9. Strong-Column/Weak Beam Frame
9

10. Avoid Shear Failure
• Ductile response requires that members yield in
flexure, and that shear failure be avoided. Shear
failure is avoided through use of a capacity-
design approach. The general approach is to
identify flexural yielding regions, design those
regions for code-required moment strengths,
and then calculate design shears based on
equilibrium assuming the flexural yielding
regions develop probable moment strengths.
10

11. Avoid Shear Failure
• Probable moment strength is calculated from
conventional flexural theory considering the as-
designed cross section, using φ = 1.0, and
assuming reinforcement yield strength equal to
at least 1.25 fy.
11

12. Detail for Ductile Behavior
• Plain concrete has relatively small usable
compressive strain capacity (around 0.003), and
this might limit the deformability of beams and
columns of special moment frames.
• Strain capacity can be increased ten-fold by
confining the concrete with reinforcing spirals or
closed hoops.
• The hoops act to restrain dilation of the core
concrete as it is loaded in compression, and this
confining action leads to increased strength and
strain capacity.
• Hoops typically are provided at the ends of
columns, as well as through beam-column joints,
and at the ends of beams.
12

13. Beams in SMRF
13

14. Beams in SMRF
• Typical economical beam span, 6 to 9 m
• Resulting beam depth that will support typical
gravity loads and requisite seismic forces
without overloading adjacent beam-column
joints and columns.
• Clear span > 4 x effective depth (ACI 21.5.1.2)
• Beams are allowed to be wider than supporting
columns, but beam width normally does not
exceed column width.
14

15. Beams in SMRF
15
Ref: ACI 318-08 Fig. R21.5.1

16. Beams in SMRF
• Divided into three different zones when
considering where hoops and stirrups can be
placed:
• At each end of the beam (2h) where flexural
yielding is expected to occur
• Needs to be well confined because this is where the
beam is expected to undergo flexural yielding and
this is the location with the highest shear.
Therefore, closely spaced, closed hoops are
required in this zone
• the zone along lap-spliced bars, if any;
• the remaining length of the beam
16

17. Beams in SMRF
17
Hoops and Stirrups Locations and Spacing Requirements

18. Beams in SMRF
18
Hoop Reinforcement Details

19. CE 72.52 – Advanced Concrete Structures - August 2012, Dr. Naveed AnwarCE 72.52 – Advanced Concrete Structures - August 2012, Dr. Naveed Anwar
• Assuming beam is yielding
in flexure, beam end
moments are set equal to
probable moment
strengths.
• Design shear is based on
the probable moment to
maintain the moment
equilibrium.
19

20. Shear Capacity of Beams
• Shear Capacity
• Assume Vc = 0 when both (a) and (b) occur:
a) The earthquake-induced shear force calculated in
accordance with ACI 21.5.4.1 represents one-half
or more of the maximum required shear strength
within yielding zones;
b) The factored axial compressive force, Pu, including
earthquake effects is less than Agfc′ /20.
20

21. Shear Capacity of Beams
• Experimental studies of reinforced concrete
members subjected to cyclic loading have
demonstrated that more shear reinforcement is
required to ensure a flexural failure if the member
is subjected to alternating nonlinear displacements
than if the member is loaded in only one direction:
the necessary increase of shear reinforcement
being higher in the case of no axial load. The
added conservatism on shear is deemed necessary
in locations where potential flexural hinging may
occur.
• However, this stratagem, chosen for its relative
simplicity, should not be interpreted to mean that
no concrete is required to resist shear.
21

22. Columns in SMRF
22

23. Columns in SMRF
• Ratio of shortest cross-sectional dimension to
perpendicular dimension not less than 0.4 (ACI
318-21.6.1.2)
• Limiting cross-section to a more compact
section rather than a long rectangle.
• Minimum column dimension = 300 mm
• Preferable minimum dimension = 400 mm,
except for unusual cases or low-rise builidngs.
23

24. Columns in SMRF
• First approximation, the columns can be
designed for the maximum factored gravity
loads while limiting the area of reinforcement
to between 1 % and 3 %.
• ACI 318 allows the longitudinal reinforcement
to reach 6 % of the gross section area, but this
amount of reinforcement results in very
congested splice locations.
24

25. Nominal Flexural Strength of Strong-
column/Weak-beam
25

26. Strong-column / Weak-beam Requirements
• In some cases it may not be practical to satisfy
the strong-column/ weak-beam provisions for
a small number of columns.
• The strength and stiffness of such columns
cannot be considered as part of the special
moment frame.
• These columns must also satisfy the
requirements of ACI 318 - 21.13, that is,
columns not designated as part of the seismic
force-resisting system.
26

27. Transverse Reinforcement
• The column transverse reinforcement should initially be
selected based on the confinement requirements of
ACI 318 - 21.6.4.
• For rectangular cross sections, the total cross-sectional
area of rectangular hoop reinforcement is not to be
less than that required by either of the following two
equations, whichever gives the larger amount.
27

28. Transverse Reinforcement
28

29. Column Design Shear
• The column design shear is defined as the larger of the
shear from procedure a and the shear from either
procedure b or procedure c.
29

30. Probable Moment for Column
30

31. Shear Capacity of Columns
• Assuming Vc = 0 when both (a) and (b) occur:
a) The earthquake-induced shear force, calculated in
accordance with 21.6.5.1, represents one-half or
more of the maximum required shear strength
within lo;
b) The factored axial compressive force, Pu, including
earthquake effects is less than Agfc′ /20.
31

32. Shear Capacity of Columns
• Length lo shall not be less than the largest of
(a), (b),and (c):
a) The depth of the member at the joint face or at
the section where flexural yielding is likely to
occur
b) One-sixth of the clear span of the member;
c) 450 mm.
32

33. Column Transverse Reinforcement Spacing
Requirements
33

34. Beam-column Joints in
SMRF
34

35. Beam-column Joints
• The frame yielding mechanism determines the
forces acting on the column and beam-column
joint.
35

36. Beam-column Joint Dimensions
• Aj is the effective cross-sectional area within a
joint computed from joint depth times effective
joint width. Joint depth shall be the overall
depth of the column, h. Effective joint width
shall be the overall width of the column, except
where a beam frames into a wider column,
effective joint width shall not exceed the
smaller of (a) and (b):
a) Beam width plus joint depth
b) Twice the smaller perpendicular distance from
longitudinal axis of beam to column side.
36

37. Beam-column Joint Dimensions
37

38. Determination of Column Shear
38

39. Determination of Joint Shear
39

40. Joint Shear Strength
40

41. 41