Fawad Najam, profile picture
Uploaded byFawad Najam
5,692 views

CE 72.32 (January 2016 Semester) Lecture 7 - Structural Analysis for Gravity Loads

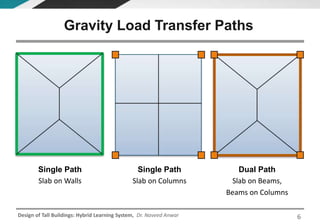
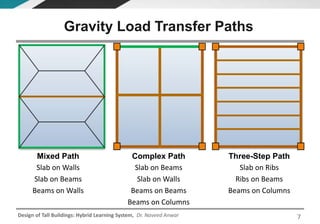
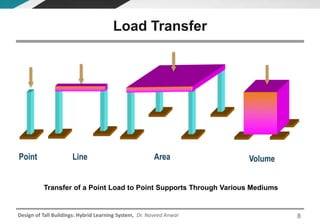
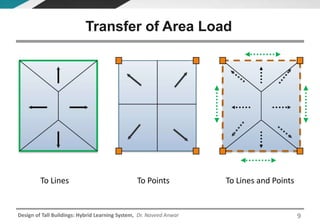
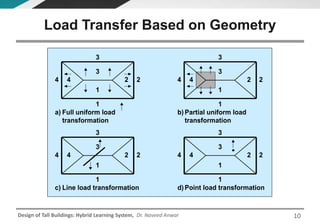
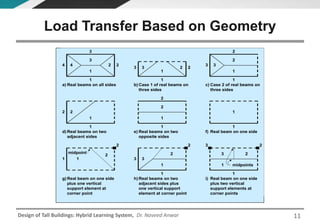
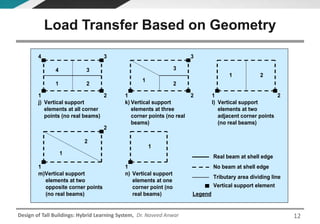
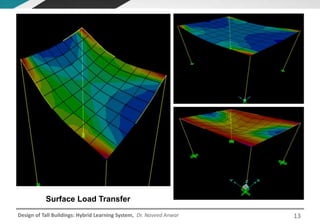
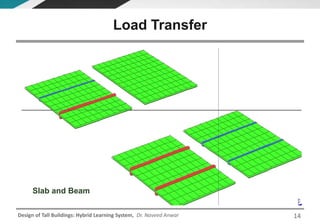
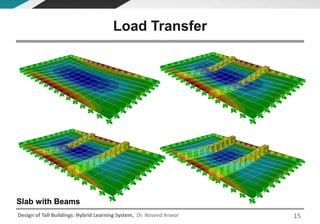
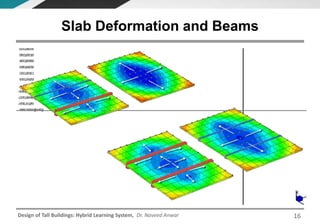
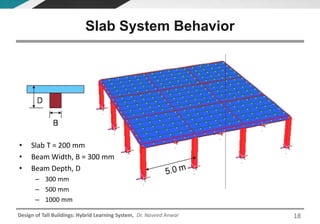
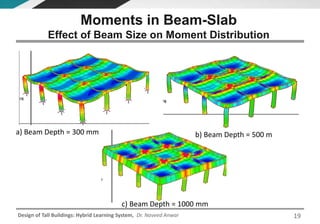
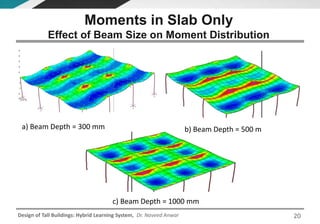
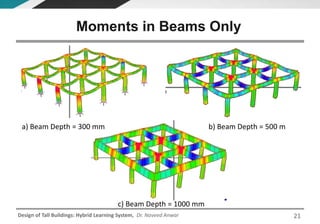
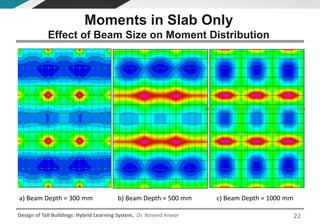
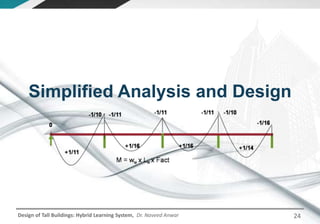
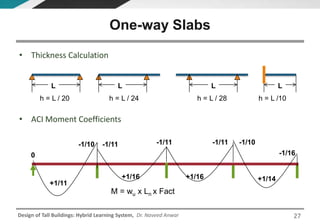
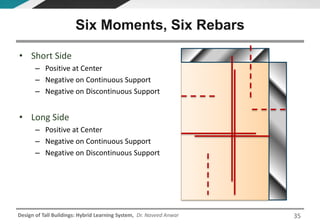
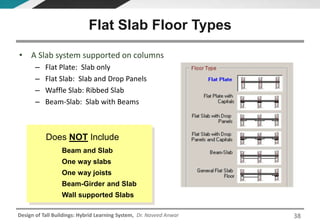
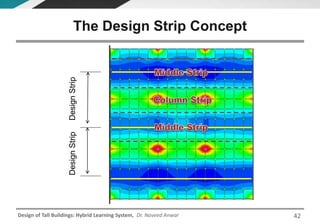
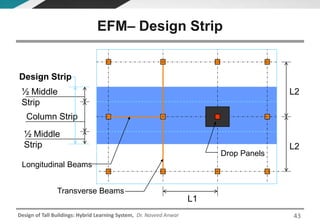
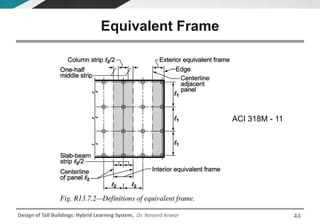
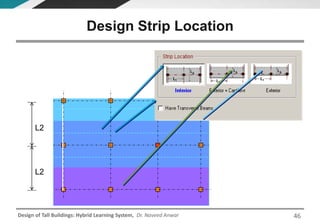
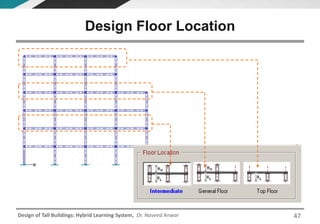
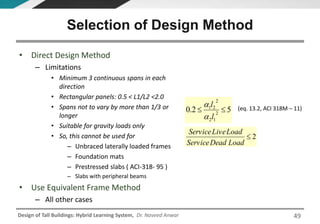
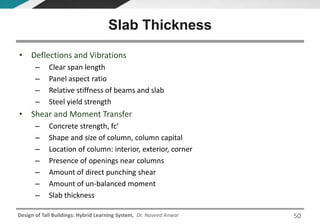
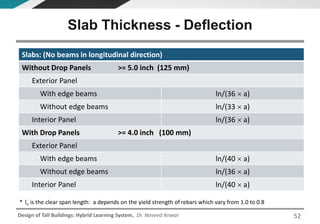
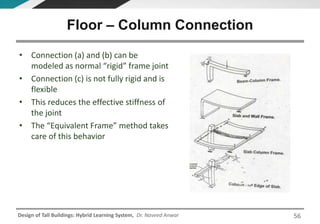
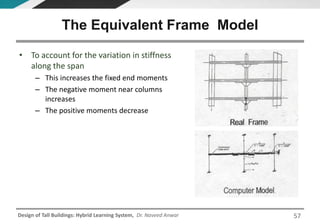
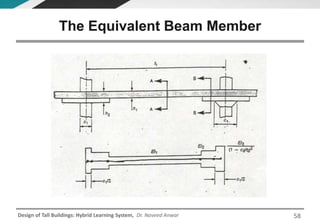
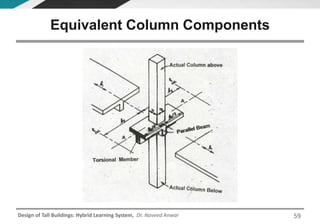
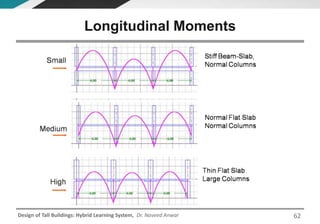
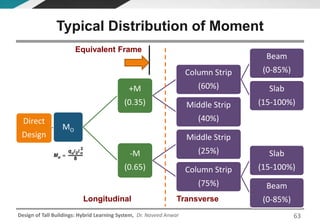
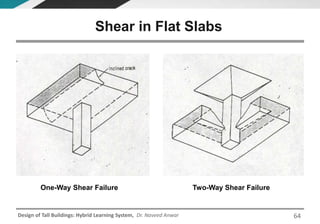
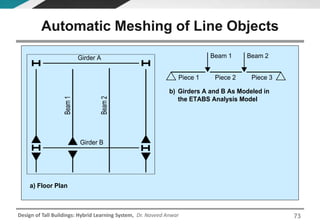
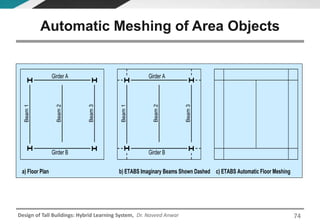
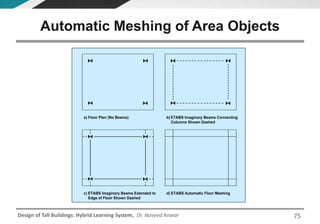
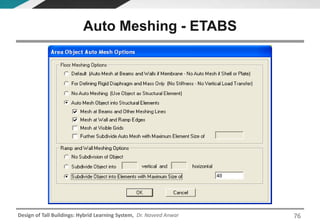
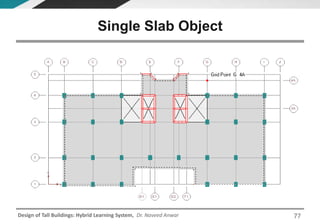
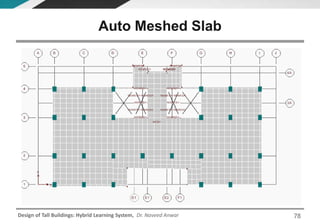
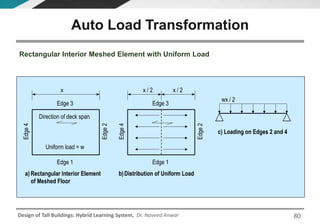
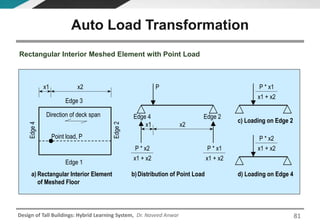
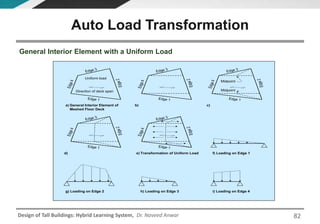
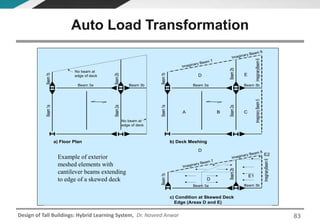
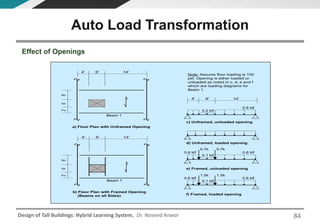
This document discusses the analysis and design of floor systems for tall buildings. It covers various types of gravity load resisting systems including direct and indirect load transfer systems. Key aspects covered include load transfer paths, behavior of slab-beam systems, importance of stiffness, simplified analysis methods for one-way and two-way slabs, and continuity conditions. Analysis approaches discussed are direct elastic analysis, moment coefficients, strip methods, yield line analysis, and finite element analysis. Design considerations include thickness estimation based on deflection and reinforcement sizing.

Embed presentation

Dr. Naveed Anwar Executive Director, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Design of Tall Buildings Hybrid Learning System
Dr. Naveed Anwar Executive Director, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Lecture 8: Structural Analysis for Gravity Loads Design of Tall Buildings
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar 3 Understanding the Behavior of Floor Systems
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Purpose – “To transfer gravity loads applied at the floor levels down to the foundation level” • Direct Path Systems – Slab supported on load bearing walls – Slab supported on columns • Indirect Multipath Systems – Slab supported on beams – Beams supported on other beams – Beams supported on walls or columns Gravity Load Resisting Systems 4
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Load Transfer Systems – Flat Slab and Flat Plate – Beam-Slab – Waffle Slab – Wall Joist • Indirect Load Transfer System – Beam, Slab – Girder, Beam, Slab – Girder, Joist Gravity Load Resting Systems 5
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar 6 Single Path Slab on Columns Dual Path Slab on Beams, Beams on Columns Single Path Slab on Walls Gravity Load Transfer Paths
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar 7 Complex Path Slab on Beams Slab on Walls Beams on Beams Beams on Columns Three-Step Path Slab on Ribs Ribs on Beams Beams on Columns Mixed Path Slab on Walls Slab on Beams Beams on Walls Gravity Load Transfer Paths
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Load Transfer Transfer of a Point Load to Point Supports Through Various Mediums Point Line Area Volume 8
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar To Points To Lines and PointsTo Lines Transfer of Area Load 9
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar a) Full uniform load transformation b) Partial uniform load transformation c) Line load transformation d) Point load transformation 1 3 24 3 24 1 1 3 24 3 24 1 1 3 24 3 24 1 1 3 24 3 24 1 Load Transfer Based on Geometry 10
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar f) Real beam on one sidee) Real beams on two opposite sides d) Real beams on two adjacent sides c) Case 2 of real beams on three sides b) Case 1 of real beams on three sides a) Real beams on all sides 1 3 24 1 3 24 1 23 1 23 1 2 3 1 2 3 1 2 1 2 1 1 1 1 2 2 i) Real beam on one side plus two vertical support elements at corner points h) Real beams on two adjacent sides plus one vertical support element at corner point g) Real beam on one side plus one vertical support element at corner point 11 1 1 1 3 1 3 2 2 2 2 midpoint 2 2 3 3 1 33 34 2 4 1 2 3 1 2 midpoints Load Transfer Based on Geometry 11
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar i) Real beam on one side plus two vertical support elements at corner points h) Real beams on two adjacent sides plus one vertical support element at corner point g) Real beam on one side plus one vertical support element at corner point 1 1 1 1 l) Vertical support elements at two adjacent corner points (no real beams) j) Vertical support elements at all corner points (no real beams) 1 1 33 3 k) Vertical support elements at three corner points (no real beams) 4 2 2 4 1 2 1 2 3 1 2 1 2 m)Vertical support elements at two opposite corner points (no real beams) 1 1 Legend Real beam at shell edge No beam at shell edge Tributary area dividing line Vertical support element midpoints n) Vertical support elements at one corner point (no real beams) 1 1 2 2 Load Transfer Based on Geometry 12
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Surface Load Transfer 13
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Slab and Beam Load Transfer 14
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Load Transfer Slab with Beams 15
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Slab Deformation and Beams 16
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • The load carried by a combination of beams and slabs depends on the relative stiffness of the beams and slabs as well as the geometric configuration • Two beams supporting the same width of slab with the same span may not carry the same load, as assumed in conventional approach • The slabs can be assumed to be resting on beams unless the beam stiffness is fairly large compared to the stiffness of the supported slab • Slab-beam stiffness ratio is specially important if some sides of the slab are supported on walls Importance of Stiffness 17
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Slab System Behavior • Slab T = 200 mm • Beam Width, B = 300 mm • Beam Depth, D – 300 mm – 500 mm – 1000 mm 18
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Beam-Slab Effect of Beam Size on Moment Distribution 19
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Slab Only Effect of Beam Size on Moment Distribution 20
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Beams Only 21
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar b) Beam Depth = 500 mm c) Beam Depth = 1000 mma) Beam Depth = 300 mm Moments in Slab Only Effect of Beam Size on Moment Distribution 22
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • The beams and slabs in a floor system act together to transfer the load to the columns. It cannot be assumed automatically that the beams will support the slab. • The moment in slabs over beam may not be negative depending on the size of panes, size of beam span beam, thickness of slabs, etc. • The ACI approach of treating all slab systems (flat slab, waffle slab, beam slab ) in a consistent manner is more realistic than designing slabs separately and beams separately Comments 23
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Simplified Analysis and Design 24
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Concepts – When Ly/Lx > 2 , one-way slabs – The load is “primarily” carried in one direction – Only Mx or My is considered – Can be considered as “Shallow Beam Strips” – Main reinforcement in one direction – Temperature/shrinkage reinforcement in other direction – Consider the “Beam Shear” case for slab shear – Used in Deck Slabs, Precast slabs, Beam and Slab One-way Slabs 25
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Design Procedure – Step 1: Model as a simple or continuous beam – Step 2: Estimate thickness based on deflection – Step 3: Analyze using coefficients or software – Step 4: Compute Reinforcement at “critical” sections – Step 5: Check thickness for shear – Step 6: Check for minimum steel and maximum spacing One-way Slabs 26
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Thickness Calculation • ACI Moment Coefficients One-way Slabs h = L / 20 L h = L / 28 h = L /10 L LL h = L / 24 0 -1/10 -1/11 -1/11 -1/11 -1/10 +1/14 +1/11 +1/16 +1/16 -1/16 M = wu x Ln x Fact 27
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Supported on edges by Walls or “Stiff Beams” • When 0.5 < Ly/Lx < 2.0 then two-way slabs • The load is “primarily” carried in two directions • Mx, My are always considered. Mxy is sometimes ignored • Main reinforcement in two orthogonal directions • Temperature/shrinkage reinforcement to be checked • Consider the “Beam Shear” as slab shear Two-way Slabs: Basic Concepts 28
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Design Procedure – Step 1: Select Analysis Method(s) – Step 2: Estimate Thickness based on Deflection – Step 3: Analyze using appropriate method or software – Step 4: Compute Reinforcement at “critical” section in two principle directions – Step 5: Check thickness for shear – Step 6: Check for minimum steel and maximum spacing Two-way Slabs 29
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Elastic Analysis – For simple geometry, boundaries and loads • Moment Coefficients – Derived for various span aspect ratio and continuity conditions – Available for rectangular and circular slabs supported on all sides • Strip Method(s) – Assume certain loads distribution pattern in each direction – Ignore Mxy and consider slab consisting of “strips” in two directions Two-way Slabs 30
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Yield Line Method – Assumes various Yield Line Patterns (Collapse or Failure” lines) – Determines capacity for each mechanism and uses the “Lowest” value • Finite Element Analysis – Models the slab using appropriate plate-shell elements – Determines Mxx, Myy and Myx at desired location Two-way Slabs 31
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Thickness-based on Deflection control • Depends on span lengths, aspect ratio, continuity conditions, steel strength etc. • Simple approach Two-way Slabs                 sideShort sideLong inch f l h y n   5.3 936 000,200 8.0 120180, toF F Perimeter h  32
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Nine Continuity Cases 33 1 2 3 4 5 6 7 8 9
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Nine Continuity Cases 1 2 9 34
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Short Side – Positive at Center – Negative on Continuous Support – Negative on Discontinuous Support • Long Side – Positive at Center – Negative on Continuous Support – Negative on Discontinuous Support Six Moments, Six Rebars 35
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Simplified Analysis and Design The Equivalent Frame Method RC Floor Slab Systems 36
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • A Slab system supported on columns – Flat Plate: Slab only – Flat Slab: Slab and Drop Panels – Waffle Slab: Ribbed Slab – Beam-Slab: Slab with Beams What is a Flat Slab System? Does NOT apply to Beam and Slab One way slabs One way joists Beam-Girder and Slab Wall-supported Slabs SystemSlabandBeam l l SystemSlabFlat l l   5 52.0 2 12 2 21 2 12 2 21     37
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • A Slab system supported on columns – Flat Plate: Slab only – Flat Slab: Slab and Drop Panels – Waffle Slab: Ribbed Slab – Beam-Slab: Slab with Beams Flat Slab Floor Types Does NOT Include Beam and Slab One way slabs One way joists Beam-Girder and Slab Wall supported Slabs 38
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Panel – Portion of a floor bounded by column, beam or wall centerlines on all sides – Includes all flexural members between column centerline • Design Strip – A continuous strip along column centerline bounded by the centerlines of the adjacent panels Components and Terminology 39
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Column Strip – Part of design strip with a minimum width of 0.25l1 and 0.25l2 on each side of a column centerline • Middle Strip – Part of design strip bounded by two adjacent column strips • Drop Panel – A thickening of slab near the column. Length must be at least L1/6 and drop thickness of at least t/4. Components and Terminology 40
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Column Capital – A diagonal head fillet around the column at the bottom of the slab. The angle should not be more than 45 degrees. • Attached Torsional Member – Portion of slab (and beam) in transverse direction attached to the column. • An Equivalent Frame – A 2D frame or a 2D sub-frame with stiffness properties of members modified to include the torsional stiffness of transverse members framing into columns. Components and Terminology 41
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar The Design Strip Concept DesignStripDesignStrip 42
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Column Strip ½ Middle Strip ½ Middle Strip Design Strip L2 L2 L1 Longitudinal Beams Transverse Beams Drop Panels EFM– Design Strip 43
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Frame 44 ACI 318M - 11
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Types – Typical interior, exterior strips – In longitudinal direction, transverse direction – Additional strips not similar to the typical • Components of Design Strip – Longitudinal Spans (in the direction of the strip) – Columns, Column Capitals, Supports – Column Strip • Slab Strips, Beams, Drop Panels – Middle Strips – Openings Selecting the Design Strips 45
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Design Strip Location L2 L2 46
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Design Floor Location 47
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Select the layout and type of slab system. • Select trial thickness for slab . • Select typical strips for design. • Choose the design method. • Compute positive and negative moments. • Distribute the moments across the width of design strip. • Design for flexure (moment reinforcement). • Check for shear and moment transfer. • Check for deflections. Main Steps 48
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Design Method – Limitations • Minimum 3 continuous spans in each direction • Rectangular panels: 0.5 < L1/L2 <2.0 • Spans not to vary by more than 1/3 or longer • Suitable for gravity loads only • So, this cannot be used for – Unbraced laterally loaded frames – Foundation mats – Prestressed slabs ( ACI-318- 95 ) – Slabs with peripheral beams • Use Equivalent Frame Method – All other cases Selection of Design Method 2 LoadDeadService LoadLiveService 52.0 2 12 2 21  l l   (eq. 13.2, ACI 318M – 11) 49
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Deflections and Vibrations – Clear span length – Panel aspect ratio – Relative stiffness of beams and slab – Steel yield strength • Shear and Moment Transfer – Concrete strength, fc’ – Shape and size of column, column capital – Location of column: interior, exterior, corner – Presence of openings near columns – Amount of direct punching shear – Amount of un-balanced moment – Slab thickness Slab Thickness 50
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Absolute Minimum Thickness – Flat plate h = 5 inch (12.5 cm) – Flat slab without drop panel h = 5 inch (12.5 cm) – Flat slab with drop panel h = 4 inch (10.0 cm) – Beam supported slabs • h = 3.5 inch (8.5 cm ) – Else 5 inch ( 12.5 cm ) • Beam Depth – Total depth Slab Thickness - Minimum 1812 11 l to l 51
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar 52 * ln is the clear span length: a depends on the yield strength of rebars which vary from 1.0 to 0.8 Slab Thickness - Deflection Slabs: (No beams in longitudinal direction) Without Drop Panels >= 5.0 inch (125 mm) Exterior Panel With edge beams ln/(36  a) Without edge beams ln/(33  a) Interior Panel ln/(36  a) With Drop Panels >= 4.0 inch (100 mm) Exterior Panel With edge beams ln/(40  a) Without edge beams ln/(36  a) Interior Panel ln/(40  a)
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Beam -Slabs Slab Thickness - Deflection     5.3 )936( 200000/8.0 0.2 0.5 ))2.0(536( 200000/8.0 0.2 2.0               yn m m yn m m fl h fl h provisionsslabuse min max n n S b m l l I I average     where 53
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Design Method (DDM) – Compute Total “Panel Design Moment, Mo – Assign Mo to supports and mid-span (-ve and +ve) – Distribute moment to various components • Equivalent Frame Method (EFM) – Create equivalent frame – Apply loads and Analyze the Frame – Obtain design moments at supports and mid-span – Distribute moment to various components Computing Design Moments 54
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Considerations – Construct over all frame – Modify properties for columns and joint zones • Analysis for lateral loads – Requires “Full” frame model – Reduced “Strip” width to account for Slab-Column connection – Simple loading • Analysis for Gravity Loads – May use Full Frame – Several load cases for pattern live load – More complex loading – Can include results of Lateral Load Analysis Equivalent Frame Method 55
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Connection (a) and (b) can be modeled as normal “rigid” frame joint • Connection (c) is not fully rigid and is flexible • This reduces the effective stiffness of the joint • The “Equivalent Frame” method takes care of this behavior Floor – Column Connection 56
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • To account for the variation in stiffness along the span – This increases the fixed end moments – The negative moment near columns increases – The positive moments decrease The Equivalent Frame Model 57
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar The Equivalent Beam Member 58
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Column Components 59
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Stiffness of Column t c c ec K K K K     1 where c ccc c l IE K  3 )1( 9 s s s cs t l C l CE K   where 3 )63.01( 3 yx y x C  Column stiffness Stiffness of attached torsional element Section torsional constant lc = length of columns Cs = Transverse dimension of column ls = Transverse span length Ecs = Modulus of slab concrete Ccc = Modulus of column concrete x = Shorter side of section parts y = Longer side of section parts Equivalent Column 60
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Stiffness of Column where where lc = length of columns Cs = Transverse dimension of column ls = Transverse span length Ecs = Modulus of slab concrete Ecc = Modulus of column concrete x = Shorter side of section parts y = Longer side of section parts t c c ec K K K K     1 c ccc c l IE K  3 )1( 9 s s s cs t l C l CE K   3 )63.01( 3 yx y x C  Column stiffness Stiffness of attached torsional element Section torsional constant Equivalent Column Stiffeness 61
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Longitudinal Moments 62
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Typical Distribution of Moment Direct Design MO +M (0.35) Column Strip (60%) Beam (0-85%) Slab (15-100%)Middle Strip (40%) -M (0.65) Middle Strip (25%) Column Strip (75%) Slab (15-100%) Beam (0-85%)Longitudinal Transverse Equivalent Frame 63
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Two-Way Shear FailureOne-Way Shear Failure Shear in Flat Slabs 64
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Assumptions and Mechanism – Concrete shear capacity based on diagonal tension – Vc (punching)  2 x Vc (beam) – “Strut-Tie” model may also be used – Capacity depends on: • Concrete strength • Shear perimeter and thickness • Shape and location of column Punching Shear for Slabs 65
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar ACI Punching Shear • Concrete Capacity, Vc • Direct Shear • Shear with Moment Transfer 2 2 1 1 c uv c uv o u u J cM J cM db V v   db V v o u u  (metric) For non prestressed slabs, Vc is smaller of, (eq.11-31,32,33 ACI 318M-11) β= Long Side/Short Side 66
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Transfer of Moment – Partially by flexure: Top or bottom bars near the column – Partially by eccentricity of shear: Non-uniform distribution of shear stresses Slab - Column Connection 2 1 3 2 1 1 b b MM fff          Cu ff Cu Cu f VVwhen portserioron columncornerVV columnedgeVVwhen portsouteredgeon      4.0 supint25.1 5.0 75.0 sup/0.1      )1( fvvv MM   67
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Provide large diameter bars at bottom within column width • Provide proper re-shoring of lower slabs • Most failure occur due to construction overload • Provide adequate punching shear strength • Use column capitals if possible • Avoid opening in the critical shear perimeter • Corner column locations are often the most critical • Provide spandrels beam or special reinforcement Prevention of Punching Failure 68
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar 69 Modeling for Gravity Loads
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Defining Individual Nodes and Elements – Using Graphical Modeling Tools to Draw Elements – Using Numerical Generation – Using Mathematical Generation – Using Copy and Replication – Using Subdivision and Meshing – Using Geometric Extrusions – Using Parametric Generation Manual Meshing Generation 70
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Draw or define the overall structure geometry in terms of physical objects • The program uses specified rules to convert objects to valid finite element mesh • Analysis is carried out using elements and the results are presented in terms of objects • Meshing does not change the number of objects in the model Automatic Meshing 71
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • Automatic Meshing of Line Objects – Where other Line Objects attach to or cross – Locations where Point Objects lie – Locations where Area objects cross • Automatic Meshing of Area Objects – Auto Meshing of area objects is much more complex than Line Objects – Area objects are meshed using several criteria and is often software dependent Automatic Meshing 72
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Girder A Girder B Beam1 Beam2 Piece 1 Piece 2 Piece 3 Beam 1 Beam 2 b) Girders A and B As Modeled in the ETABS Analysis Model a) Floor Plan Automatic Meshing of Line Objects 73
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Girder A Girder B Beam1 Beam2 Beam3 Girder A Girder B Beam1 Beam2 Beam3 c) ETABS Automatic Floor Meshingb) ETABS Imaginary Beams Shown Dasheda) Floor Plan Automatic Meshing of Area Objects 74
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar d) ETABS Automatic Floor Meshing b) ETABS Imaginary Beams Connecting Columns Shown Dashed a) Floor Plan (No Beams) c) ETABS Imaginary Beams Extended to Edge of Floor Shown Dashed Automatic Meshing of Area Objects 75
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Auto Meshing - ETABS 76
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Single Slab Object 77
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Auto Meshed Slab 78
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar • In contrast to slab sections which are assumed to span in two directions, the load distribution for deck sections is one way • ETABS first automatically meshes the deck into quadrilateral elements • Once the meshing is complete, ETABS determines the meshed shell elements that have real beams along them and those that have imaginary beams • It also determines which edges of the meshed shell elements are also edges of the deck. Auto Load Transformation 79
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Edge 1 Edge 3 Edge2 Edge4 x Edge 1 Edge 3 Edge2 Edge4 x / 2 x / 2 Uniform load = w Direction of deck span a) Rectangular Interior Element of Meshed Floor b)Distribution of Uniform Load wx / 2 c) Loading on Edges 2 and 4 Rectangular Interior Meshed Element with Uniform Load Auto Load Transformation 80
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Edge 1 Edge 3 Edge2 Edge4 x1 x2 Point load, P Direction of deck span a) Rectangular Interior Element of Meshed Floor b)Distribution of Point Load x1 x2 Edge 4 Edge 2 P P * x2 x1 + x2 P * x1 x1 + x2 c) Loading on Edge 2 P * x1 x1 + x2 d) Loading on Edge 4 P * x2 x1 + x2 Rectangular Interior Meshed Element with Point Load Auto Load Transformation 81
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar d) Edge 1 Edge 3 Edge2 Edge4 Edge 1 Edge 3 Edge2 Edge4 e) Transformation of Uniform Load Edge 1 Edge 3 Edge2 Edge4 Uniform load Direction of deck span a) General Interior Element of Meshed Floor Deck b) Edge 1 Edge 3 Edge2 Edge4 Edge 1 Edge 3 Edge2 Edge4 c) g) Loading on Edge 2 f) Loading on Edge 1 h) Loading on Edge 3 i) Loading on Edge 4 Midpoint Midpoint General Interior Element with a Uniform Load Auto Load Transformation 82
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar Imaginary Beam 8 a) Floor Plan b) Deck Meshing B CA ED ImaginaryBeam5ImaginaryBeam6 Beam 3a Beam 3b Beam1aBeam1b Beam2aBeam2b Beam 3a Beam 3b Beam1aBeam1b Beam2aBeam2b Imaginary Beam 7 Imaginary Beam 8 E1 ImaginaryBeam6 Beam 3b Beam2b E2 c) Condition at Skewed Deck Edge (Areas D and E) Imaginary Beam 7 D D Beam 3a Beam1b No beam at edge of deck No beam at edge of deck Example of exterior meshed elements with cantilever beams extending to edge of a skewed deck Auto Load Transformation 83
Design of Tall Buildings: Hybrid Learning System, Dr. Naveed Anwar a) Floor Plan with Unframed Opening Beam 1 4' 6' 14' 6'4'2' b) Floor Plan with Framed Opening (Beams on all Sides) Beam 1 4' 6' 14' 6'4'2' c) Unframed, unloaded opening 4' 6' 14' Note: Assume floor loading is 100 psf. Opening is either loaded or unloaded as noted in c, d, e and f which are loading diagrams for Beam 1. d) Unframed, loaded opening e) Framed, unloaded opening f) Framed, loaded opening 0.7k 0.6 klf 0.2 klf 0.6 klf 0.6 klf 0.6 klf 0.6 klf 0.1 klf 0.1 klf 0.7k 1.5k 1.5k Effect of Openings Auto Load Transformation 84
Dr. Naveed Anwar Executive Director, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Thank You

More Related Content

PPTX
CE 72.32 (January 2016 Semester) Lecture 8 - Structural Analysis for Lateral ...
byFawad Najam
 
PDF
CE 72.32 (January 2016 Semester): Lecture 1b: Analysis and Design of Tall Bui...
byFawad Najam
 
PPTX
CE 72.32 (January 2016 Semester) Lecture 2 - Design Philosophy
byFawad Najam
 
PPTX
CE 72.32 (January 2016 Semester) Lecture 5 - Preliminary Design and Sizing
byFawad Najam
 
PDF
CE 72.32 (January 2016 Semester) Lecture 3 - Design Criteria
byFawad Najam
 
PPTX
CE 72.32 (January 2016 Semester) Lecture 6 - Overview of Finite Element Analysis
byFawad Najam
 
PDF
Performance Based Design, Value Engineering and Peer Review by Dr. Naveed Anwar
byAIT Solutions
 
PPSX
CE 72.52 - Lecture 8a - Retrofitting of RC Members
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 8 - Structural Analysis for Lateral ...
byFawad Najam
 
CE 72.32 (January 2016 Semester): Lecture 1b: Analysis and Design of Tall Bui...
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 2 - Design Philosophy
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 5 - Preliminary Design and Sizing
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 3 - Design Criteria
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 6 - Overview of Finite Element Analysis
byFawad Najam
 
Performance Based Design, Value Engineering and Peer Review by Dr. Naveed Anwar
byAIT Solutions
 
CE 72.52 - Lecture 8a - Retrofitting of RC Members
byFawad Najam
 

What's hot

PPTX
CE72.52 - Lecture 3a - Section Behavior - Flexure
byFawad Najam
 
PPTX
CE 72.32 (January 2016 Semester): Lecture 1a - Overview of Tall Buildings
byFawad Najam
 
PDF
Conceptual Design in Structural System Development
byAIT Solutions
 
PPTX
CE72.52 - Lecture1 - Introduction
byFawad Najam
 
PDF
Recent Trends and Advancement in Performance Assessment of RC High-Rise Build...
byAIT Solutions
 
PPTX
AITC Shear Wall Design Procedure (20151106)
byFawad Najam
 
PPTX
CE72.52 - Lecture 3b - Section Behavior - Shear and Torsion
byFawad Najam
 
PPTX
CE 72.32 (January 2016 Semester) Lecture 4 - Selection of Structural Systems
byFawad Najam
 
PDF
Dynamic Response
byAIT Solutions
 
PPTX
AITC Coupling Beam Design Procedure (20151106)
byFawad Najam
 
PPSX
CE 72.52 - Lecture 8b - Retrofitting of RC Members
byFawad Najam
 
PDF
Structural Design of Bridges
byAIT Solutions
 
PPTX
CE 72.52 - Lecture 5 - Column Design
byFawad Najam
 
PDF
Integrated Performance Based Design of Tall Buildings for Wind and Earthquake...
byAIT Solutions
 
PDF
Progression of Structural Design Approaches by Dr. Naveed Anwar
byAIT Solutions
 
PDF
3.4 pushover analysis
byNASRIN AFROZ
 
PDF
Importance of Ductility in Structural Performance Analysis
byAIT Solutions
 
PDF
CASE STUDY: PERFORMANCE-BASED SEISMIC DESIGN OF REINFORCED CONCRETE DUAL SYST...
byAIT Solutions
 
PPTX
CE 72.52 - Lecture 7 - Strut and Tie Models
byFawad Najam
 
PDF
Cost Effective Structural Configurations For Tall Buildings by Dr. Naveed Anwar
byAIT Solutions
 
CE72.52 - Lecture 3a - Section Behavior - Flexure
byFawad Najam
 
CE 72.32 (January 2016 Semester): Lecture 1a - Overview of Tall Buildings
byFawad Najam
 
Conceptual Design in Structural System Development
byAIT Solutions
 
CE72.52 - Lecture1 - Introduction
byFawad Najam
 
Recent Trends and Advancement in Performance Assessment of RC High-Rise Build...
byAIT Solutions
 
AITC Shear Wall Design Procedure (20151106)
byFawad Najam
 
CE72.52 - Lecture 3b - Section Behavior - Shear and Torsion
byFawad Najam
 
CE 72.32 (January 2016 Semester) Lecture 4 - Selection of Structural Systems
byFawad Najam
 
Dynamic Response
byAIT Solutions
 
AITC Coupling Beam Design Procedure (20151106)
byFawad Najam
 
CE 72.52 - Lecture 8b - Retrofitting of RC Members
byFawad Najam
 
Structural Design of Bridges
byAIT Solutions
 
CE 72.52 - Lecture 5 - Column Design
byFawad Najam
 
Integrated Performance Based Design of Tall Buildings for Wind and Earthquake...
byAIT Solutions
 
Progression of Structural Design Approaches by Dr. Naveed Anwar
byAIT Solutions
 
3.4 pushover analysis
byNASRIN AFROZ
 
Importance of Ductility in Structural Performance Analysis
byAIT Solutions
 
CASE STUDY: PERFORMANCE-BASED SEISMIC DESIGN OF REINFORCED CONCRETE DUAL SYST...
byAIT Solutions
 
CE 72.52 - Lecture 7 - Strut and Tie Models
byFawad Najam
 
Cost Effective Structural Configurations For Tall Buildings by Dr. Naveed Anwar
byAIT Solutions
 

Similar to CE 72.32 (January 2016 Semester) Lecture 7 - Structural Analysis for Gravity Loads

PDF
Etabs modelling parameters
byEur Ing Valentinos Neophytou BEng (Hons), MSc, CEng MICE
 
PDF
Reinforced concrete slab design principles and analysis techniques
bytixi6884
 
PPTX
PRESENTATION 3 - Copy.pptx
bykuba9
 
PDF
Structural Engineering Solutions to Architectural (and other) Challenges by D...
byAIT Solutions
 
PDF
IRJET- A Performance Study of High Raise Building with Flat Slab System u...
byIRJET Journal
 
PDF
flat slab - moment.pdf for structural engineer's
byEndalkazene
 
PDF
IRJET- A Study on Performance of High-Rise Building with different Struct...
byIRJET Journal
 
PPTX
Design of Flat Slab and Bridges
byAnanthakumar75
 
DOCX
Analysis and Design of Mid-Rise Building_2023.docx
byadnan885140
 
DOCX
Analysis and Design of Mid-Rise Building_2023.docx
byAdnan Lazem
 
PPT
Design of tall buildings lecture-1-part-2-dr-shafiul-bari-sir
byjibonghosh
 
PDF
Design & Analysis of Multi-storied Building under Static and Dynamic Loading ...
byIRJET Journal
 
PDF
Design of Steel Grillage Foundation for an Auditorium
byIRJET Journal
 
DOCX
NCIT civil Syllabus 2013-2014
byLAKSHITHA RAJAPAKSHA
 
PDF
IRJET- Comparative Study of Flat slab and Beam-Slab System for a Multi-Stori...
byIRJET Journal
 
PPTX
Struds overview
bySreedinesh Sridharan
 
PPTX
Conceptual-Designadwdad-of-Structures.pptx
byRoux38
 
PDF
IRJET - Economy in Building Construction Systems of Prefabricated Structures
byIRJET Journal
 
PPTX
Analysis and design of 15 storey office and
byMasroor Alam
 
PPTX
Analysis and design of 15 storey office and
byMasroor Alam
 
Etabs modelling parameters
byEur Ing Valentinos Neophytou BEng (Hons), MSc, CEng MICE
 
Reinforced concrete slab design principles and analysis techniques
bytixi6884
 
PRESENTATION 3 - Copy.pptx
bykuba9
 
Structural Engineering Solutions to Architectural (and other) Challenges by D...
byAIT Solutions
 
IRJET- A Performance Study of High Raise Building with Flat Slab System u...
byIRJET Journal
 
flat slab - moment.pdf for structural engineer's
byEndalkazene
 
IRJET- A Study on Performance of High-Rise Building with different Struct...
byIRJET Journal
 
Design of Flat Slab and Bridges
byAnanthakumar75
 
Analysis and Design of Mid-Rise Building_2023.docx
byadnan885140
 
Analysis and Design of Mid-Rise Building_2023.docx
byAdnan Lazem
 
Design of tall buildings lecture-1-part-2-dr-shafiul-bari-sir
byjibonghosh
 
Design & Analysis of Multi-storied Building under Static and Dynamic Loading ...
byIRJET Journal
 
Design of Steel Grillage Foundation for an Auditorium
byIRJET Journal
 
NCIT civil Syllabus 2013-2014
byLAKSHITHA RAJAPAKSHA
 
IRJET- Comparative Study of Flat slab and Beam-Slab System for a Multi-Stori...
byIRJET Journal
 
Struds overview
bySreedinesh Sridharan
 
Conceptual-Designadwdad-of-Structures.pptx
byRoux38
 
IRJET - Economy in Building Construction Systems of Prefabricated Structures
byIRJET Journal
 
Analysis and design of 15 storey office and
byMasroor Alam
 
Analysis and design of 15 storey office and
byMasroor Alam
 

More from Fawad Najam

PDF
An Introduction to ABAQUS CAE
byFawad Najam
 
PDF
Introduction to Capacity-based Seismic Design
byFawad Najam
 
PPTX
CE 72.52 - Lecture6 - Member Behavior
byFawad Najam
 
PPTX
CE 72.52 Lecture 4 - Ductility of Cross-sections
byFawad Najam
 
PDF
Introduction to SPSS v20
byFawad Najam
 
PPTX
CE72.52 - Lecture 2 - Material Behavior
byFawad Najam
 
PDF
Basic Video Editing Training for Beginners
byFawad Najam
 
PDF
Basic DSLR Photography and Videography for AITians
byFawad Najam
 
An Introduction to ABAQUS CAE
byFawad Najam
 
Introduction to Capacity-based Seismic Design
byFawad Najam
 
CE 72.52 - Lecture6 - Member Behavior
byFawad Najam
 
CE 72.52 Lecture 4 - Ductility of Cross-sections
byFawad Najam
 
Introduction to SPSS v20
byFawad Najam
 
CE72.52 - Lecture 2 - Material Behavior
byFawad Najam
 
Basic Video Editing Training for Beginners
byFawad Najam
 
Basic DSLR Photography and Videography for AITians
byFawad Najam
 

Recently uploaded

PDF
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
PDF
Shear Strength of Soil/Mohr Coulomb Failure Criteria-1.pdf
byMahmoodKhalid11
 
PDF
Ericsson 6230 Training Module Document.pdf
byMd Bellal Hossain
 
PDF
Soil Compressibility (Elastic Settlement).pdf
byMahmoodKhalid11
 
PPTX
Introduction to AI and Applications Module-4.pptx
byKalaiselviSubramania2
 
PPTX
Data Link Layer Unit II Computer Networks.pptx
bylosstwolf17
 
PDF
Manual de instalacion de notifire NFS320
byMarcoPolitoPerez
 
PPTX
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
PPTX
The Most Controversial TPM Debate in Maintenance Today Checklist TPM vs Outco...
byMaintWiz Technologies Private Limited
 
PPTX
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
PPTX
Designing Work for Humans, Not Machines: Human-Centered Maintenance Excellence
byMaintWiz Technologies Private Limited
 
PDF
Rajesh Prasad- Brief Profile with educational, professional highlights
byRajesh Prasad
 
PPTX
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
PPTX
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
PDF
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
PDF
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
PDF
Python programming basics Unit-1 for R25 regulation
byssuser492e7f
 
PPTX
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
PPTX
uADPF Topology_SFP requirements_locked slides.pptx
byMd Bellal Hossain
 
PPTX
Week 2.1.pptxdynamics particle kinetics introduction 2
byfmsalih06
 
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
Shear Strength of Soil/Mohr Coulomb Failure Criteria-1.pdf
byMahmoodKhalid11
 
Ericsson 6230 Training Module Document.pdf
byMd Bellal Hossain
 
Soil Compressibility (Elastic Settlement).pdf
byMahmoodKhalid11
 
Introduction to AI and Applications Module-4.pptx
byKalaiselviSubramania2
 
Data Link Layer Unit II Computer Networks.pptx
bylosstwolf17
 
Manual de instalacion de notifire NFS320
byMarcoPolitoPerez
 
Why TPM Succeeds in Some Plants and Struggles in Others | MaintWiz
byMaintWiz Technologies Private Limited
 
The Most Controversial TPM Debate in Maintenance Today Checklist TPM vs Outco...
byMaintWiz Technologies Private Limited
 
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
Designing Work for Humans, Not Machines: Human-Centered Maintenance Excellence
byMaintWiz Technologies Private Limited
 
Rajesh Prasad- Brief Profile with educational, professional highlights
byRajesh Prasad
 
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
Python programming basics Unit-1 for R25 regulation
byssuser492e7f
 
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
uADPF Topology_SFP requirements_locked slides.pptx
byMd Bellal Hossain
 
Week 2.1.pptxdynamics particle kinetics introduction 2
byfmsalih06
 

CE 72.32 (January 2016 Semester) Lecture 7 - Structural Analysis for Gravity Loads

  • 1.
    Dr. Naveed Anwar ExecutiveDirector, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Design of Tall Buildings Hybrid Learning System
  • 2.
    Dr. Naveed Anwar ExecutiveDirector, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Lecture 8: Structural Analysis for Gravity Loads Design of Tall Buildings
  • 3.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar 3 Understanding the Behavior of Floor Systems
  • 4.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Purpose – “To transfer gravity loads applied at the floor levels down to the foundation level” • Direct Path Systems – Slab supported on load bearing walls – Slab supported on columns • Indirect Multipath Systems – Slab supported on beams – Beams supported on other beams – Beams supported on walls or columns Gravity Load Resisting Systems 4
  • 5.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Load Transfer Systems – Flat Slab and Flat Plate – Beam-Slab – Waffle Slab – Wall Joist • Indirect Load Transfer System – Beam, Slab – Girder, Beam, Slab – Girder, Joist Gravity Load Resting Systems 5
  • 6.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar 6 Single Path Slab on Columns Dual Path Slab on Beams, Beams on Columns Single Path Slab on Walls Gravity Load Transfer Paths
  • 7.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar 7 Complex Path Slab on Beams Slab on Walls Beams on Beams Beams on Columns Three-Step Path Slab on Ribs Ribs on Beams Beams on Columns Mixed Path Slab on Walls Slab on Beams Beams on Walls Gravity Load Transfer Paths
  • 8.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Load Transfer Transfer of a Point Load to Point Supports Through Various Mediums Point Line Area Volume 8
  • 9.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar To Points To Lines and PointsTo Lines Transfer of Area Load 9
  • 10.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar a) Full uniform load transformation b) Partial uniform load transformation c) Line load transformation d) Point load transformation 1 3 24 3 24 1 1 3 24 3 24 1 1 3 24 3 24 1 1 3 24 3 24 1 Load Transfer Based on Geometry 10
  • 11.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar f) Real beam on one sidee) Real beams on two opposite sides d) Real beams on two adjacent sides c) Case 2 of real beams on three sides b) Case 1 of real beams on three sides a) Real beams on all sides 1 3 24 1 3 24 1 23 1 23 1 2 3 1 2 3 1 2 1 2 1 1 1 1 2 2 i) Real beam on one side plus two vertical support elements at corner points h) Real beams on two adjacent sides plus one vertical support element at corner point g) Real beam on one side plus one vertical support element at corner point 11 1 1 1 3 1 3 2 2 2 2 midpoint 2 2 3 3 1 33 34 2 4 1 2 3 1 2 midpoints Load Transfer Based on Geometry 11
  • 12.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar i) Real beam on one side plus two vertical support elements at corner points h) Real beams on two adjacent sides plus one vertical support element at corner point g) Real beam on one side plus one vertical support element at corner point 1 1 1 1 l) Vertical support elements at two adjacent corner points (no real beams) j) Vertical support elements at all corner points (no real beams) 1 1 33 3 k) Vertical support elements at three corner points (no real beams) 4 2 2 4 1 2 1 2 3 1 2 1 2 m)Vertical support elements at two opposite corner points (no real beams) 1 1 Legend Real beam at shell edge No beam at shell edge Tributary area dividing line Vertical support element midpoints n) Vertical support elements at one corner point (no real beams) 1 1 2 2 Load Transfer Based on Geometry 12
  • 13.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Surface Load Transfer 13
  • 14.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Slab and Beam Load Transfer 14
  • 15.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Load Transfer Slab with Beams 15
  • 16.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Slab Deformation and Beams 16
  • 17.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • The load carried by a combination of beams and slabs depends on the relative stiffness of the beams and slabs as well as the geometric configuration • Two beams supporting the same width of slab with the same span may not carry the same load, as assumed in conventional approach • The slabs can be assumed to be resting on beams unless the beam stiffness is fairly large compared to the stiffness of the supported slab • Slab-beam stiffness ratio is specially important if some sides of the slab are supported on walls Importance of Stiffness 17
  • 18.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Slab System Behavior • Slab T = 200 mm • Beam Width, B = 300 mm • Beam Depth, D – 300 mm – 500 mm – 1000 mm 18
  • 19.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Beam-Slab Effect of Beam Size on Moment Distribution 19
  • 20.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Slab Only Effect of Beam Size on Moment Distribution 20
  • 21.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar c) Beam Depth = 1000 mm b) Beam Depth = 500 ma) Beam Depth = 300 mm Moments in Beams Only 21
  • 22.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar b) Beam Depth = 500 mm c) Beam Depth = 1000 mma) Beam Depth = 300 mm Moments in Slab Only Effect of Beam Size on Moment Distribution 22
  • 23.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • The beams and slabs in a floor system act together to transfer the load to the columns. It cannot be assumed automatically that the beams will support the slab. • The moment in slabs over beam may not be negative depending on the size of panes, size of beam span beam, thickness of slabs, etc. • The ACI approach of treating all slab systems (flat slab, waffle slab, beam slab ) in a consistent manner is more realistic than designing slabs separately and beams separately Comments 23
  • 24.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Simplified Analysis and Design 24
  • 25.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Concepts – When Ly/Lx > 2 , one-way slabs – The load is “primarily” carried in one direction – Only Mx or My is considered – Can be considered as “Shallow Beam Strips” – Main reinforcement in one direction – Temperature/shrinkage reinforcement in other direction – Consider the “Beam Shear” case for slab shear – Used in Deck Slabs, Precast slabs, Beam and Slab One-way Slabs 25
  • 26.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Design Procedure – Step 1: Model as a simple or continuous beam – Step 2: Estimate thickness based on deflection – Step 3: Analyze using coefficients or software – Step 4: Compute Reinforcement at “critical” sections – Step 5: Check thickness for shear – Step 6: Check for minimum steel and maximum spacing One-way Slabs 26
  • 27.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Thickness Calculation • ACI Moment Coefficients One-way Slabs h = L / 20 L h = L / 28 h = L /10 L LL h = L / 24 0 -1/10 -1/11 -1/11 -1/11 -1/10 +1/14 +1/11 +1/16 +1/16 -1/16 M = wu x Ln x Fact 27
  • 28.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Supported on edges by Walls or “Stiff Beams” • When 0.5 < Ly/Lx < 2.0 then two-way slabs • The load is “primarily” carried in two directions • Mx, My are always considered. Mxy is sometimes ignored • Main reinforcement in two orthogonal directions • Temperature/shrinkage reinforcement to be checked • Consider the “Beam Shear” as slab shear Two-way Slabs: Basic Concepts 28
  • 29.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Design Procedure – Step 1: Select Analysis Method(s) – Step 2: Estimate Thickness based on Deflection – Step 3: Analyze using appropriate method or software – Step 4: Compute Reinforcement at “critical” section in two principle directions – Step 5: Check thickness for shear – Step 6: Check for minimum steel and maximum spacing Two-way Slabs 29
  • 30.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Elastic Analysis – For simple geometry, boundaries and loads • Moment Coefficients – Derived for various span aspect ratio and continuity conditions – Available for rectangular and circular slabs supported on all sides • Strip Method(s) – Assume certain loads distribution pattern in each direction – Ignore Mxy and consider slab consisting of “strips” in two directions Two-way Slabs 30
  • 31.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Yield Line Method – Assumes various Yield Line Patterns (Collapse or Failure” lines) – Determines capacity for each mechanism and uses the “Lowest” value • Finite Element Analysis – Models the slab using appropriate plate-shell elements – Determines Mxx, Myy and Myx at desired location Two-way Slabs 31
  • 32.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Thickness-based on Deflection control • Depends on span lengths, aspect ratio, continuity conditions, steel strength etc. • Simple approach Two-way Slabs                 sideShort sideLong inch f l h y n   5.3 936 000,200 8.0 120180, toF F Perimeter h  32
  • 33.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Nine Continuity Cases 33 1 2 3 4 5 6 7 8 9
  • 34.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Nine Continuity Cases 1 2 9 34
  • 35.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Short Side – Positive at Center – Negative on Continuous Support – Negative on Discontinuous Support • Long Side – Positive at Center – Negative on Continuous Support – Negative on Discontinuous Support Six Moments, Six Rebars 35
  • 36.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Simplified Analysis and Design The Equivalent Frame Method RC Floor Slab Systems 36
  • 37.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • A Slab system supported on columns – Flat Plate: Slab only – Flat Slab: Slab and Drop Panels – Waffle Slab: Ribbed Slab – Beam-Slab: Slab with Beams What is a Flat Slab System? Does NOT apply to Beam and Slab One way slabs One way joists Beam-Girder and Slab Wall-supported Slabs SystemSlabandBeam l l SystemSlabFlat l l   5 52.0 2 12 2 21 2 12 2 21     37
  • 38.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • A Slab system supported on columns – Flat Plate: Slab only – Flat Slab: Slab and Drop Panels – Waffle Slab: Ribbed Slab – Beam-Slab: Slab with Beams Flat Slab Floor Types Does NOT Include Beam and Slab One way slabs One way joists Beam-Girder and Slab Wall supported Slabs 38
  • 39.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Panel – Portion of a floor bounded by column, beam or wall centerlines on all sides – Includes all flexural members between column centerline • Design Strip – A continuous strip along column centerline bounded by the centerlines of the adjacent panels Components and Terminology 39
  • 40.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Column Strip – Part of design strip with a minimum width of 0.25l1 and 0.25l2 on each side of a column centerline • Middle Strip – Part of design strip bounded by two adjacent column strips • Drop Panel – A thickening of slab near the column. Length must be at least L1/6 and drop thickness of at least t/4. Components and Terminology 40
  • 41.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Column Capital – A diagonal head fillet around the column at the bottom of the slab. The angle should not be more than 45 degrees. • Attached Torsional Member – Portion of slab (and beam) in transverse direction attached to the column. • An Equivalent Frame – A 2D frame or a 2D sub-frame with stiffness properties of members modified to include the torsional stiffness of transverse members framing into columns. Components and Terminology 41
  • 42.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar The Design Strip Concept DesignStripDesignStrip 42
  • 43.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Column Strip ½ Middle Strip ½ Middle Strip Design Strip L2 L2 L1 Longitudinal Beams Transverse Beams Drop Panels EFM– Design Strip 43
  • 44.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Frame 44 ACI 318M - 11
  • 45.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Types – Typical interior, exterior strips – In longitudinal direction, transverse direction – Additional strips not similar to the typical • Components of Design Strip – Longitudinal Spans (in the direction of the strip) – Columns, Column Capitals, Supports – Column Strip • Slab Strips, Beams, Drop Panels – Middle Strips – Openings Selecting the Design Strips 45
  • 46.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Design Strip Location L2 L2 46
  • 47.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Design Floor Location 47
  • 48.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Select the layout and type of slab system. • Select trial thickness for slab . • Select typical strips for design. • Choose the design method. • Compute positive and negative moments. • Distribute the moments across the width of design strip. • Design for flexure (moment reinforcement). • Check for shear and moment transfer. • Check for deflections. Main Steps 48
  • 49.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Design Method – Limitations • Minimum 3 continuous spans in each direction • Rectangular panels: 0.5 < L1/L2 <2.0 • Spans not to vary by more than 1/3 or longer • Suitable for gravity loads only • So, this cannot be used for – Unbraced laterally loaded frames – Foundation mats – Prestressed slabs ( ACI-318- 95 ) – Slabs with peripheral beams • Use Equivalent Frame Method – All other cases Selection of Design Method 2 LoadDeadService LoadLiveService 52.0 2 12 2 21  l l   (eq. 13.2, ACI 318M – 11) 49
  • 50.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Deflections and Vibrations – Clear span length – Panel aspect ratio – Relative stiffness of beams and slab – Steel yield strength • Shear and Moment Transfer – Concrete strength, fc’ – Shape and size of column, column capital – Location of column: interior, exterior, corner – Presence of openings near columns – Amount of direct punching shear – Amount of un-balanced moment – Slab thickness Slab Thickness 50
  • 51.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Absolute Minimum Thickness – Flat plate h = 5 inch (12.5 cm) – Flat slab without drop panel h = 5 inch (12.5 cm) – Flat slab with drop panel h = 4 inch (10.0 cm) – Beam supported slabs • h = 3.5 inch (8.5 cm ) – Else 5 inch ( 12.5 cm ) • Beam Depth – Total depth Slab Thickness - Minimum 1812 11 l to l 51
  • 52.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar 52 * ln is the clear span length: a depends on the yield strength of rebars which vary from 1.0 to 0.8 Slab Thickness - Deflection Slabs: (No beams in longitudinal direction) Without Drop Panels >= 5.0 inch (125 mm) Exterior Panel With edge beams ln/(36  a) Without edge beams ln/(33  a) Interior Panel ln/(36  a) With Drop Panels >= 4.0 inch (100 mm) Exterior Panel With edge beams ln/(40  a) Without edge beams ln/(36  a) Interior Panel ln/(40  a)
  • 53.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Beam -Slabs Slab Thickness - Deflection     5.3 )936( 200000/8.0 0.2 0.5 ))2.0(536( 200000/8.0 0.2 2.0               yn m m yn m m fl h fl h provisionsslabuse min max n n S b m l l I I average     where 53
  • 54.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Direct Design Method (DDM) – Compute Total “Panel Design Moment, Mo – Assign Mo to supports and mid-span (-ve and +ve) – Distribute moment to various components • Equivalent Frame Method (EFM) – Create equivalent frame – Apply loads and Analyze the Frame – Obtain design moments at supports and mid-span – Distribute moment to various components Computing Design Moments 54
  • 55.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Considerations – Construct over all frame – Modify properties for columns and joint zones • Analysis for lateral loads – Requires “Full” frame model – Reduced “Strip” width to account for Slab-Column connection – Simple loading • Analysis for Gravity Loads – May use Full Frame – Several load cases for pattern live load – More complex loading – Can include results of Lateral Load Analysis Equivalent Frame Method 55
  • 56.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Connection (a) and (b) can be modeled as normal “rigid” frame joint • Connection (c) is not fully rigid and is flexible • This reduces the effective stiffness of the joint • The “Equivalent Frame” method takes care of this behavior Floor – Column Connection 56
  • 57.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • To account for the variation in stiffness along the span – This increases the fixed end moments – The negative moment near columns increases – The positive moments decrease The Equivalent Frame Model 57
  • 58.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar The Equivalent Beam Member 58
  • 59.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Column Components 59
  • 60.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Stiffness of Column t c c ec K K K K     1 where c ccc c l IE K  3 )1( 9 s s s cs t l C l CE K   where 3 )63.01( 3 yx y x C  Column stiffness Stiffness of attached torsional element Section torsional constant lc = length of columns Cs = Transverse dimension of column ls = Transverse span length Ecs = Modulus of slab concrete Ccc = Modulus of column concrete x = Shorter side of section parts y = Longer side of section parts Equivalent Column 60
  • 61.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Equivalent Stiffness of Column where where lc = length of columns Cs = Transverse dimension of column ls = Transverse span length Ecs = Modulus of slab concrete Ecc = Modulus of column concrete x = Shorter side of section parts y = Longer side of section parts t c c ec K K K K     1 c ccc c l IE K  3 )1( 9 s s s cs t l C l CE K   3 )63.01( 3 yx y x C  Column stiffness Stiffness of attached torsional element Section torsional constant Equivalent Column Stiffeness 61
  • 62.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Longitudinal Moments 62
  • 63.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Typical Distribution of Moment Direct Design MO +M (0.35) Column Strip (60%) Beam (0-85%) Slab (15-100%)Middle Strip (40%) -M (0.65) Middle Strip (25%) Column Strip (75%) Slab (15-100%) Beam (0-85%)Longitudinal Transverse Equivalent Frame 63
  • 64.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Two-Way Shear FailureOne-Way Shear Failure Shear in Flat Slabs 64
  • 65.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Basic Assumptions and Mechanism – Concrete shear capacity based on diagonal tension – Vc (punching)  2 x Vc (beam) – “Strut-Tie” model may also be used – Capacity depends on: • Concrete strength • Shear perimeter and thickness • Shape and location of column Punching Shear for Slabs 65
  • 66.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar ACI Punching Shear • Concrete Capacity, Vc • Direct Shear • Shear with Moment Transfer 2 2 1 1 c uv c uv o u u J cM J cM db V v   db V v o u u  (metric) For non prestressed slabs, Vc is smaller of, (eq.11-31,32,33 ACI 318M-11) β= Long Side/Short Side 66
  • 67.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Transfer of Moment – Partially by flexure: Top or bottom bars near the column – Partially by eccentricity of shear: Non-uniform distribution of shear stresses Slab - Column Connection 2 1 3 2 1 1 b b MM fff          Cu ff Cu Cu f VVwhen portserioron columncornerVV columnedgeVVwhen portsouteredgeon      4.0 supint25.1 5.0 75.0 sup/0.1      )1( fvvv MM   67
  • 68.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Provide large diameter bars at bottom within column width • Provide proper re-shoring of lower slabs • Most failure occur due to construction overload • Provide adequate punching shear strength • Use column capitals if possible • Avoid opening in the critical shear perimeter • Corner column locations are often the most critical • Provide spandrels beam or special reinforcement Prevention of Punching Failure 68
  • 69.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar 69 Modeling for Gravity Loads
  • 70.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Defining Individual Nodes and Elements – Using Graphical Modeling Tools to Draw Elements – Using Numerical Generation – Using Mathematical Generation – Using Copy and Replication – Using Subdivision and Meshing – Using Geometric Extrusions – Using Parametric Generation Manual Meshing Generation 70
  • 71.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Draw or define the overall structure geometry in terms of physical objects • The program uses specified rules to convert objects to valid finite element mesh • Analysis is carried out using elements and the results are presented in terms of objects • Meshing does not change the number of objects in the model Automatic Meshing 71
  • 72.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • Automatic Meshing of Line Objects – Where other Line Objects attach to or cross – Locations where Point Objects lie – Locations where Area objects cross • Automatic Meshing of Area Objects – Auto Meshing of area objects is much more complex than Line Objects – Area objects are meshed using several criteria and is often software dependent Automatic Meshing 72
  • 73.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Girder A Girder B Beam1 Beam2 Piece 1 Piece 2 Piece 3 Beam 1 Beam 2 b) Girders A and B As Modeled in the ETABS Analysis Model a) Floor Plan Automatic Meshing of Line Objects 73
  • 74.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Girder A Girder B Beam1 Beam2 Beam3 Girder A Girder B Beam1 Beam2 Beam3 c) ETABS Automatic Floor Meshingb) ETABS Imaginary Beams Shown Dasheda) Floor Plan Automatic Meshing of Area Objects 74
  • 75.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar d) ETABS Automatic Floor Meshing b) ETABS Imaginary Beams Connecting Columns Shown Dashed a) Floor Plan (No Beams) c) ETABS Imaginary Beams Extended to Edge of Floor Shown Dashed Automatic Meshing of Area Objects 75
  • 76.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Auto Meshing - ETABS 76
  • 77.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Single Slab Object 77
  • 78.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Auto Meshed Slab 78
  • 79.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar • In contrast to slab sections which are assumed to span in two directions, the load distribution for deck sections is one way • ETABS first automatically meshes the deck into quadrilateral elements • Once the meshing is complete, ETABS determines the meshed shell elements that have real beams along them and those that have imaginary beams • It also determines which edges of the meshed shell elements are also edges of the deck. Auto Load Transformation 79
  • 80.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Edge 1 Edge 3 Edge2 Edge4 x Edge 1 Edge 3 Edge2 Edge4 x / 2 x / 2 Uniform load = w Direction of deck span a) Rectangular Interior Element of Meshed Floor b)Distribution of Uniform Load wx / 2 c) Loading on Edges 2 and 4 Rectangular Interior Meshed Element with Uniform Load Auto Load Transformation 80
  • 81.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Edge 1 Edge 3 Edge2 Edge4 x1 x2 Point load, P Direction of deck span a) Rectangular Interior Element of Meshed Floor b)Distribution of Point Load x1 x2 Edge 4 Edge 2 P P * x2 x1 + x2 P * x1 x1 + x2 c) Loading on Edge 2 P * x1 x1 + x2 d) Loading on Edge 4 P * x2 x1 + x2 Rectangular Interior Meshed Element with Point Load Auto Load Transformation 81
  • 82.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar d) Edge 1 Edge 3 Edge2 Edge4 Edge 1 Edge 3 Edge2 Edge4 e) Transformation of Uniform Load Edge 1 Edge 3 Edge2 Edge4 Uniform load Direction of deck span a) General Interior Element of Meshed Floor Deck b) Edge 1 Edge 3 Edge2 Edge4 Edge 1 Edge 3 Edge2 Edge4 c) g) Loading on Edge 2 f) Loading on Edge 1 h) Loading on Edge 3 i) Loading on Edge 4 Midpoint Midpoint General Interior Element with a Uniform Load Auto Load Transformation 82
  • 83.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar Imaginary Beam 8 a) Floor Plan b) Deck Meshing B CA ED ImaginaryBeam5ImaginaryBeam6 Beam 3a Beam 3b Beam1aBeam1b Beam2aBeam2b Beam 3a Beam 3b Beam1aBeam1b Beam2aBeam2b Imaginary Beam 7 Imaginary Beam 8 E1 ImaginaryBeam6 Beam 3b Beam2b E2 c) Condition at Skewed Deck Edge (Areas D and E) Imaginary Beam 7 D D Beam 3a Beam1b No beam at edge of deck No beam at edge of deck Example of exterior meshed elements with cantilever beams extending to edge of a skewed deck Auto Load Transformation 83
  • 84.
    Design of TallBuildings: Hybrid Learning System, Dr. Naveed Anwar a) Floor Plan with Unframed Opening Beam 1 4' 6' 14' 6'4'2' b) Floor Plan with Framed Opening (Beams on all Sides) Beam 1 4' 6' 14' 6'4'2' c) Unframed, unloaded opening 4' 6' 14' Note: Assume floor loading is 100 psf. Opening is either loaded or unloaded as noted in c, d, e and f which are loading diagrams for Beam 1. d) Unframed, loaded opening e) Framed, unloaded opening f) Framed, loaded opening 0.7k 0.6 klf 0.2 klf 0.6 klf 0.6 klf 0.6 klf 0.6 klf 0.1 klf 0.1 klf 0.7k 1.5k 1.5k Effect of Openings Auto Load Transformation 84
  • 85.
    Dr. Naveed Anwar ExecutiveDirector, AIT Consulting Affiliated Faculty, Structural Engineering Director, ACECOMS Thank You