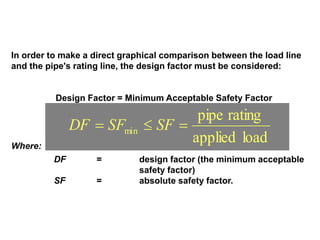
The document discusses factors related to casing design, including: 1) The design factor is the minimum acceptable safety factor, which is the ratio of the load applied to the pipe's rating. 2) The axial strength of the pipe is determined by an equation using the pipe's minimum yield strength, outer diameter, and inner diameter. 3) A triaxial stress criterion using three stress components - axial, tangential, and radial - is presented for evaluating combined loading conditions. Loads falling within the resulting design envelope meet the design criteria.

1. Casing Design

2. Design Factors
In order to make a direct graphical comparison between the load line
and the pipe's rating line, the design factor must be considered:
Design Factor = Minimum Acceptable Safety Factor
Where:
DF = design factor (the minimum acceptable
safety factor)
SF = absolute safety factor.
loadapplied
ratingpipe
min  SFSFDF

3. Axial Equation
The axial strength of the pipe body is determined by the pipe
body yield strength formula found in API Bulletin 5C3.
Where:
Fy = pipe body axial strength (units of
force).
Yp = minimum yield strength.
D = nominal outer diameter.
d = nominal inner diameter.
Q: Why 87.5% is not considered in this Eq?
  py YdDF 22
4



4. Axial Equation
The axial strength of the pipe body is determined by the pipe
body yield strength formula found in API Bulletin 5C3.
Where:
Fy = pipe body axial strength (units of
force).
Yp = minimum yield strength.
D = nominal outer diameter.
d = nominal inner diameter.
Q: Why 87.5% is not considered in this Eq?
  py YdDF 22
4



5. Axial Equation
The axial strength of the pipe body is determined by the pipe
body yield strength formula found in API Bulletin 5C3.
Where:
Fy = pipe body axial strength (units of
force).
Yp = minimum yield strength.
D = nominal outer diameter.
d = nominal inner diameter.
Q: Why 87.5% is not considered in this Eq?
  py YdDF 22
4



6. von Mises Criterion:
Where:
Yp = minimum yield strength.
VME = triaxial stress.
z = axial stress.
 = tangential or hoop stress.
r = radial stress.
r

z
       21222
2
1
zrrzVMEpY   

7. Triaxial Design Ellipse
Plotting the loads on this ellipse allows a direct comparison of the triaxial
criterion with the API ratings.
Loads that fall within the design envelope meet the design criteria.

8. Understanding the Triaxial design ellipse
• Combined compression and burst loading corresponds to the upper left-hand
quadrant of the design envelope. This is the region where triaxial analysis is most
critical because reliance on the uniaxial criteria alone would not predict several
possible failures.
• Combined tension and burst loading corresponds to the upper right-hand
quadrant of the design envelope. This is the region where reliance on the uniaxial
criteria alone may result in a design which is more conservative than necessary.
• For most pipes used in the oilfield, collapse is an instability failure independent of
material yield. The triaxial criterion is based on elastic behavior and the yield
strength of the material and hence, should not be used with collapse loads. The
one exception is for thick wall pipes with a low D/t ratio which have an API rating
in the yield strength collapse region. This collapse criterion along with the effects
of tension and internal pressure (which are triaxial effects) result in the API
criterion being essentially identical to the triaxial method in the lower right-hand
quadrant of the triaxial ellipse for thick wall pipes.
• For high compression and moderate collapse loads experienced in the lower left-
hand quadrant of the design envelope, the failure mode is permanent
corkscrewing due to helical buckling. It is appropriate to use the triaxial criterion
in this case.