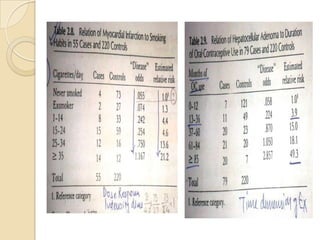
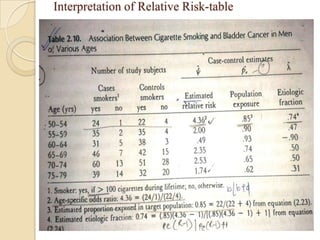
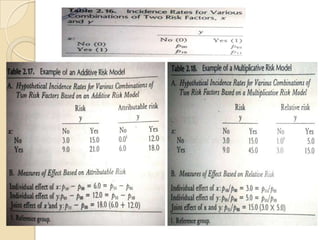
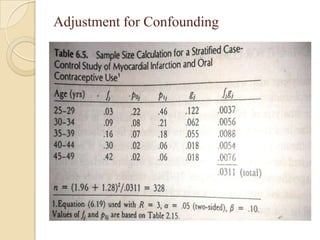
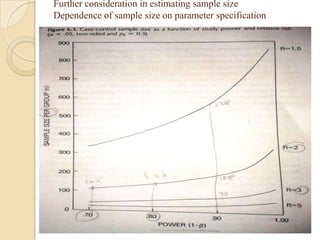
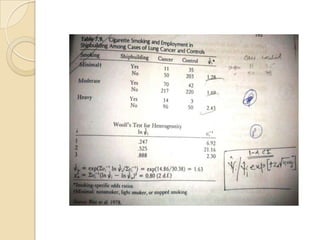
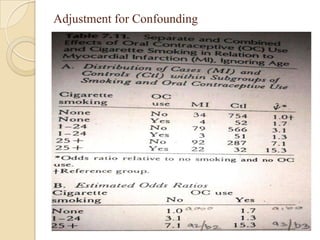
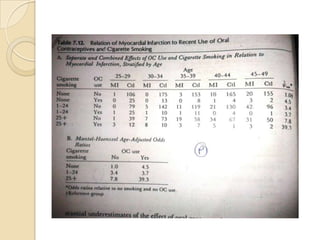
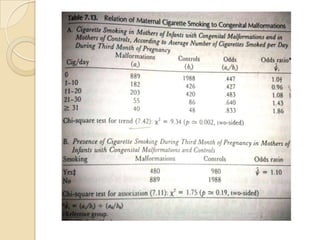
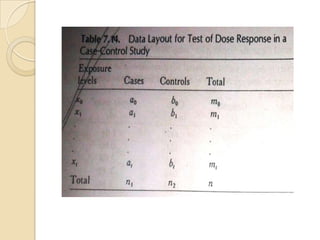
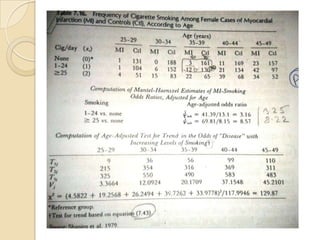
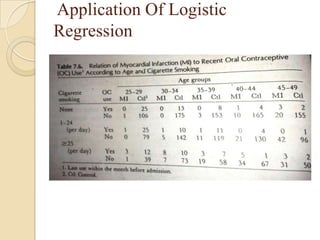
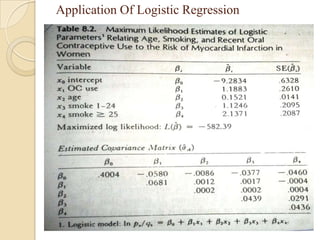
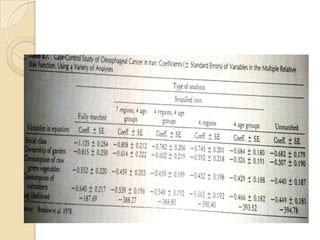
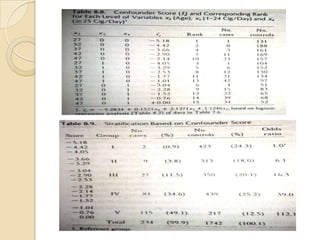
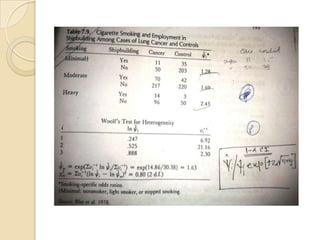
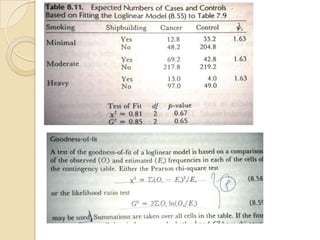
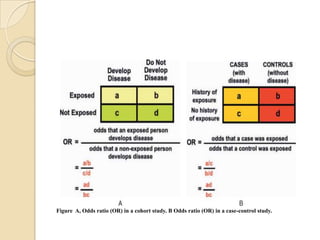
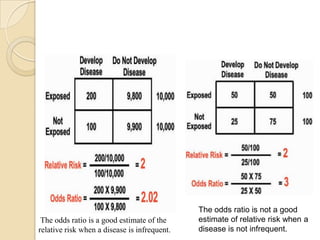
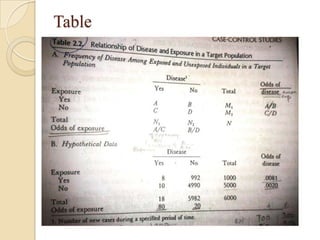
This document provides an outline and overview of key concepts in case-control study design and analysis. It discusses topics such as measures of disease occurrence, relative risk, sample size calculation, methods for adjusting for confounding, and multivariate analysis techniques including logistic regression and log-linear models. The goal is to introduce the basic methodology for case-control studies and analyzing associations between disease outcomes and exposures of interest.

1. Case control study - Part 2
Dr. Rizwan S A, M.D.,

2. Outline





Basic Concepts in the Assessment of Risk
Sample Size
Basic Method of Analysis
Multivariate Analysis
Nested Case-Control

3. Basic Concepts in the Assessment of
Risk
Disease Occurrence
 Relative Measures of Disease Occurrence
 Cohort and Case-Control Sampling Schemes
 Risk of Disease Attributable to Exposure
 Exposure
 Interpretation of Relative Risk
 Cumulative Risk of Disease
 Association and Testing for Significance
 Relative Risk as a measure of the Strength Of
Association
 Confounding
 Interaction
 Summary


4. Disease Occurrence
•
Cumulative Incidence
Number of persons with disease onset during a specified
period
Number of persons at risk in the beginning of the period
• Incidence Rate
Number of new disease events in a specified period
The sum of the subjects disease free time of follow up during
this period
• Prevalence
Number of persons with a disease at a certain point intime
Number of persons in the population at that point in time

5. Relative Measures of Disease Occurrence

Relative Risk: the ratio of the risk of disease in exposed
individuals to the risk of disease in non exposed
individuals.
Odds Ratio Ψ
The odds of an event can be defined as the ratio of the
number of ways the event can occur to the number of
ways the event cannot occur
Case Control study can’t determine IR of disease ass. with
+/- study exposure ,it can estimate the ratio of IR (RR)
in terms of Odds Ratio
•

6. Figure A, Odds ratio (OR) in a cohort study. B Odds ratio (OR) in a case-control study.

7. When Odds ratio a good estimate of
RR?
1. When the cases studied are representative, with regard to
history of exposure, of all people with the disease in the
population from which the cases were drawn.
2. When the controls studied are representative, with regard to
history of exposure, of all people without the disease in the
population from which the cases were drawn.
3. When the disease being studied does not occur frequently.

8. The odds ratio is a good estimate of the
relative risk when a disease is infrequent.
The odds ratio is not a good
estimate of relative risk when a
disease is not infrequent.

9. Table

10. Cohort Sampling-Table

The incidence rates/relative risk/odds of dis. among
exposed /non exposed estimated from sample agree with
the values in target population but odds of exposure are
different in both.

11. Case-Control sampling-Table

The proportion of incident cases among exposed /non
exposed individual in sample is different from target
population , but odds of exposure are same

12. Risk of Disease Attributable to Exposure
Q.How much of the disease that occurs can be attributed to
a certain exposure?
A.The attributable risk,defined as the amount or proportion
of disease incidence (or disease risk) that can be
attributed to a specific exposure(δ)
OR
δ=p1-p2 =(R-1)p2≈(Ψ-1)p2

13. Exposure-Specific Risk
IR for entire populations (p) are a weighted avg. of ExposureSpecific rates p1 and p2,
 pe=M1/N
 p=N1/N
 p=p1pe +p2(1-pe)
 p1=Rp2
 p2=p/{Rpe+(1-pe)}
 p̂2 = ̂p/{ ̂Ψ ̂pe+(1-̂pe)}
 P̂1= ̂Ψp̂2
 P(D/Ei)=P(Ei/D)P(D)/ P(Ei/D)P(D)+P(Ei/D̅)P(D̅)
The exp-sp prob of dis. can be determined given estimate of
overall probability of dis and proportion of cases and controls
in ith exp category.

14. Etiologic Fraction –Table1
λ =proportion of all cases in the target population
attributable to exposure.
 λ =N1-Np2/N1
 λ= pe(R-1)/[pe(R-1)+1]
 eg-Table
 p2=p(1- λ); p1= Rp(1- λ)


16. Exposure-table
Intensity dimension
 Time dimension
 Estimation of Population Exposure Rate From Control
Series

 Control series must be representative of individual without dis. In
target population
 Dis. must be rare.
Unconditional prob of ex in target population=weighted
avg of cond.prob of ex among dis. and non-dis.
P(E)= P(E/D)P(D)+P(E/D̅)P(D̅)
If P(D) ≈0,P(D̅) ≈1; P(E)=P(E/D̅) ,(rare- pê ,̂̂ Ψ )
λ̂= pê (̂̂Ψ -1)/[pê (̂̂ Ψ -1)+1]


18. Interpretation of Relative Risk-table

20. Relative risk as a measure of strength of
association

If X uncontrolled var. which doesn’t interact with E
accounts for all the risk due to E;R>1
• X must be R times more common among E/NE;
P(X/E)>RP(X/E̅)
• X must be as strong a risk facto as the E
•
Presence of multiple real causes reduces the apparent
relative risk for any one of them

21. Interaction-Table
Effect modification tells us that the association between
exposure and disease is modified by a third factor.
 When IR of a dis. in presence of 2 or > risk factors
differs from IR resulting from combination of their
individual effects-Interaction

◦ Synergism or Antagonism special case of Positive and Negative
Interaction .
◦ Additive
 (p11-p00)=(p10-p00)+(p01-p00)
 (Rxy-1)=(Rx-1)+(Ry-1)
◦ Multiplicative
 p11/p00=(p10/p00)(p01/p00)
 Rxy=RxRy

23. Sample Size








Sample Size and Power for Unmatched Studies
Sample Size and Power with Multiple Control
per Case
Smallest detectable Relative Risk
Optimal Allocation
Adjustment for Confounding
Sample Size and Power for Pair-Matched
Studies
Sequential Case-Control Studies
Summary

24. Sample size-Inroduction

Study should be large to avoid:
◦ Claiming that E is associated with D when it is not- α
◦ E is not associated with D when it is- β
 Probability of finding the sampling estimate of RR(OR) differs
sig. from unity=1- β=Power

How many subjects for case control
study(matched/unmatched)?
◦
◦
◦
◦
Relative frequency of E among controls in target population-p0
Hypothesized RR associated with E of public health imp-R
Desired level of Significance- α
Desired study power, 1- β

25. Sample Size and Power for
Unmatched Studies

26. Sample Size and Power for Unmatched
Studies

28. Sample Size and Power for Unmatched
Studies

29. Sample Size and Power with Multiple Control
per Case-With unequal controls per case

30. Sample Size and Power with Multiple
Control per Case-With unequal controls per
case

31. Sample Size and Power with Multiple
Control per Case-With unequal controls per
case

32. Smallest detectable Relative Risk

Given fixed n,a,p0;what is smallest R can be detected
with specified power?

33. Optimal Allocation

Equal Case-control cost

34. Optimal Allocation

Unequal cost: Max power for fixed total cost

35. Unequal cost: Max power for fixed total cost

36. Optimal Allocation

Minimum cost for Fixed Power

37. Adjustment for Confounding

Sample size for Case control study that use stratified
analysis to adjust for confounding must specify
◦ RR
◦ Estimated exposure rate among controls in each of k
strata po1,p02 etc
◦ Estimated proportion of cases in each strata f1,f2
◦ Significance- α
◦ power, 1- β
Eg-

38. Adjustment for Confounding

39. Adjustment for Confounding

40. Sample Size and Power for Pair-Matched
Studies
Exposed (+) ,Unexposed (-)
 Case, control(++)(+-)(--)(-+)
◦ For specified α,β no. of discordant pairs required for RR


41. Sample Size and Power for Pair-Matched
Studies

42. Sample Size and Power for Pair-Matched
Studies

43. Sequential Case-Control Studies
Rather than waiting until a predetermined no. of cases and
controls have accumulated it proceeds as data become
available over time.
 Sample size<for fixed sample size analysis.
 Data collection continues until one either obtains a significant
case-control difference or until one reaches a predetermined
maximum no of stages , S.


eg

45. Further consideration in estimating sample
size

Adjustment for Non response
◦ If rate of non response=r*100 percent,
◦ no of subjects to obtain final series size: na= n/1-r
◦ Eg-150/.85=177

Sub group analysis

46. Sub group analysis

47. 
Multiple control per case
If c control per case n’≈(c+1)n/2c1

48. Further consideration in estimating sample size
Dependence of sample size on parameter specification

49. Further consideration in estimating sample size

Dependence of sample size on parameter specification

50. Basic Method of Analysis









Unmatched Analysis of a Single 2*2 table
Adjustment for Confounding
Assessment of Individual and Joint Effects of Two
or More Variables
Test for Dose Response
Test-Based Control Limits
Matched Analysis with One Control Per Case
Matched Analysis with Two Control per Case
Matched Analysis with Three or more Control per
Case
Estimation of the Etiologic Fraction

51. Unmatched Analysis of a Single 2*2 table

55. Adjustment for confounding



If OR-constant across subgroups/consistently
elevated/reduced=combine them to form a summary
estimate.
Summary Estimate as having been adjusted for effects of
variables used in stratification.
Methods for obtaining point estimates , test of
significance , CI for summary OR
◦ Mantel-Haenszel Method-weighted avg of individual OR
◦ Wolfes Method-constant OR across subgroup

57. 
Mantel-Haenszel method

63. Test for Heterogeneity of OR

65. Assessment of Individual and Joint Effects
of Two or More Variables-tab
CI/test of sig=same
 Test of heterogeneity and Confidence limits are
diff.
 Adjustment for confounding-table`1


67. Adjustment for Confounding

69. Test for Dose Response-tab

Trend with Dose response
Trend with severity of dis.
Adjustment for comnfounding-tab

Test based confidence limits



73. *-

76. Matched Analysis with One Control
Per Case

77. Matched Analysis with One Control Per
Case-*


Test for sig and CI
Probability of exposed case is estimated by p=b/b+c

79. Matched Analysis with Two Control Per Case

80. Test of sig ,CI

81. Matched Analysis with Three /more
Control Per Case

83. Estimation of the Etiologic Fraction

Unmatched study with dichotomous E

85. Multivariate Analysis






Logistic Regression For Case-Control Studies
Estimation of Logistic Parameter
Application Of Logistic Regression
Matched Analysis
Confounder Score
Log linear Models

86. Introduction

Analysis concerned with the variability of a
Dependent variable related to multiple
Explanatory var.

87. Logistic Regression For Case-Control Studies

93. Estimation of Logistic Parameter

Discriminant Analysis
◦ to isolate relevant risk factors in a logistic model by tests of sig

94. Maximum Likelihood Estimation
To estimate the actual magnitude of parameters or probability of
events under the logistic model.

95. 
CI and Test of Sig.

96. Application Of Logistic
Regression

97. Application Of Logistic Regression

100. Matched Analysis
Matched
 Unmatched analysis of Matched data?


105. Confounder Score-tab




Each case and control is assigned a score that indicates
how ‘caselike’ that a person is estimated to be in absence
of exposure to study factor.
Each individual is assigned to one of strata
Stratum specific OR
Combined estimate by M-H method.

107. Log linear Models

Approach to analyze Case-control data when all var. are
discrete-categorical/continuous have been stratified.

112. Thank You