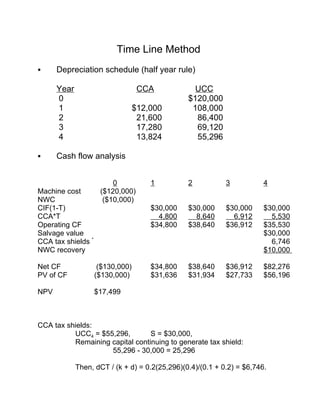
The document explains capital budgeting formulas and provides an example to illustrate how to calculate net present value (NPV). It shows the steps to determine cash flows, tax shields, salvage value, and changes in net working capital in present value terms. The key steps are: 1) determine cash outflows and inflows over the project life, 2) calculate tax shields from capital cost allowance, 3) account for salvage value and changes in working capital. The example is worked through using both a timeline method and formula method to demonstrate the calculations.

1. Capital Budgeting Formula
C Not in the book. Wei’s summary
C If salvage value S is less than UCCn:
C If salvage value S is greater than UCCn:
Note: ICFt: incremental cash flows (could be negative)
)(NWC): change in net working capital. Positive if
additional WC required for a year; negative if
WC is released for a year.

2. Year CCA UCC
0 $200,000
1 $30,000 $170,000
2 $51,000 $119,000
3 $35,700 $83,300
Explaining the Capital Budgeting Formula
Let’s use the following example to illustrate the formulas. Suppose you have a project
which requires an initial investment (in a piece of equipment) of $200,000. The equipment
has a CCA rate of 0.3. The project will last 3 years. At the end of year 3, the equipment will
be sold for $35,000. The project will reduce production cost by $110,000 per year. The
initial working capital requirement is $25,000. An additional amount of $8,000 is required
for year 1. All will be recovered at the end of year 3. The tax rate is 40% and the discount
rate is 10%. What is the NPV?
Let’s first get the CCA schedule using the half-year rule:
Since the salvage value S = $35,000 is less than UCC3 = $83,300, we use the first formula:
Let’s examine one item at a time.
1) The first item is initial investment. C = $200,000. Since it is an investment or cash
outflow, we have a negative sign in front it.
2) The second item is the total PV of after tax, incremental cash flows (ICF). It is the
net benefit of having a project. In our case, the savings in costs are just like
increases in revenues. So, each ICF = $110,000. The entire second item can be
written as
110,000(1-0.4)/(1+0.1) + 110,000*(1-0.4)/(1+0.1)2
+ 110,000*(1-0.4)/(1+0.1)3
=$109,421. Since this is a benefit, we have a positive sign in front it.
3) The third item is the net working capital. The summation goes from time zero to year
n. Notice that we only keep track of the changes (hence the greek letter ∆). In other
words, we only worry about the net addition and reductions. In our case, the initial
requirement is $25,000, so ∆(NWC)1 = $25,000. The second year, we need another
$8,000, so ∆(NWC)1 = $8,000. No new requirement or recovery in the second year,
so ∆(NWC)2 = 0. By year 3, we will recover everything, which means ∆(NWC)3 = -
$33,000. (This is $25,000 + $8,000). Why the negative sign in front of $33,000?
Because this is not additional requirement, rather, it is the recovery, the opposite of

3. investment. Now, there is a negative sign in front of the who third item. This is to
reflect the fact that a positive NWC represents an investment or a cash outflow. So,
the entire third item is
25,000 + 8,000/(1+0.1) - 33,000/(1+0.1)3
= $7,479
In other words, in PV terms we need to invest $7,470 in NWC (this is the financing
cost).
Since NWC is cash outflow, we have a negative sign in front it.
4) The fourth item is simply the PV of salvage value, which is
35,000/(1+0.1)3
= $26,296
We have a positive sign in front of it, since this is cash inflow.
5) The fifth item is the PV of all the future tax shields from CCA assuming the
equipment will last forever, under the half-year rule. It is
0.3*(200,000)(0.4)/(0.1+0.4)*[(1+0.5*0.1)/(1+0.1)] = $57,273.
We have a positive sign in front of it, since this is tax savings.
6) The last item is the tax shield adjustment. When we calculate item 5, we assume
that the equipment would last forever. But we know that we will lose it after three
years. Therefore, we will not be able to enjoy CCA tax shields after year three. We
must subtract an amount from item 5 to reflect this lost. At the end of year 3, the
UCC is $83,300 and the salvage value is $35,000. If the equipment is not sold and
is held forever, then you would continue to depreciate $83,300 from year 3 on. No
adjustment is needed in this case, since item 5 is the case of equipment lasting
forever. But when you sell it for $35,000, you have recovered $35,000, only the
remaining amount (which is $83,300 - $35,000 = $48,300) will continue to generate
tax shields forever. In other words, you will lose $35,000 (which is salvage value, S)
from the capital base. Since this is lost forever, so the present value of tax shields
from this amount is dST/(k+d) (here we don’t use the half-year formula anymore
since it is year 3 already). What about 1/(1+k)n
? This is simply to bring the PV of tax
shield loss to today. In our case, the entire sixth item is
1/(1+0.1)3
[0.3*35,000*0.4/(0.1+0.3)] = $7,889.
We have a negative sign in front of it, since we lose it.
Put all items together:
NPV = -$200,000 + $109,421 - $7,479 + $26,296 + $57,273 - $7,889
= - $22,378
****************
If we change the example just by one number: make the salvage value to be
$90,000. In this case, since S > UCC3, we will use the second formula. Why? Since
by selling the equipment, you will have recovered all the remaining book value of the
equipment ($83,300). You should not enjoy any CCA tax shields from that point on.
That is why we put the entire UCC in the formula.
Anyway, in this case, we only need to adjust the fourth item (which is now
$90000/(1.1)3
= $67,618) and the last item (which is now 1/(1+0.1)3
[0.3*83,300*0.4/(0.1+0.3)] = $18,775). So the new NPV is
NPV = -$200,000 + $109,421 - $7,479 + $67,618 + $57,273 - $18,775
= $8,058

4. Example
A new machine:
CCA class: 8 (d=20%)
Life 4 years
Price $100,000
Freight & installation: $20,000
Salvage value: $30,000
Additional NWC: $10,000
Effect on costs: decrease costs
by $50,000 per year
Tax rate: 40%
Cost of capital (k): 10%
Depreciation base:
C = $100,000 + $20,000
= $120,000
(No additional NWC required during life. But in general, NWC
changes every year)

5. Time Line Method
C Depreciation schedule (half year rule)
Year CCA UCC
0 $120,000
1 $12,000 108,000
2 21,600 86,400
3 17,280 69,120
4 13,824 55,296
C Cash flow analysis
0 1 2 3 4
Machine cost ($120,000)
NWC ($10,000)
CIF(1-T) $30,000 $30,000 $30,000 $30,000
CCA*T 4,800 8,640 6,912 5,530
Operating CF $34,800 $38,640 $36,912 $35,530
Salvage value $30,000
CCA tax shields *
6,746
NWC recovery $10,000
Net CF ($130,000) $34,800 $38,640 $36,912 $82,276
PV of CF ($130,000) $31,636 $31,934 $27,733 $56,196
NPV $17,499
CCA tax shields:
UCC4 = $55,296, S = $30,000,
Remaining capital continuing to generate tax shield:
55,296 - 30,000 = 25,296
Then, dCT / (k + d) = 0.2(25,296)(0.4)/(0.1 + 0.2) = $6,746.

6. Formula Method
C Depreciation schedule (half year rule)
Year CCA UCC
0 $120,000
1 $12,000 108,000
2 21,600 86,400
3 17,280 69,120
4 13,824 55,296
C UCC4 = $55,296 > S =$30,000, Therefore use
C = $120,000
)(NWC)0 = $10,000 )(NWC)t = 0 (T = 1, 2, 3)
)(NWC)4 = - $10,000
ICFt = 50,000 (t = 1,4) S = $30,000
T = 0.4 d = 0.2
k = 0.1 n = 4
NPV = $17,499

7. What if salvage value is $60,000? Everything else remains the same.
The Time Line Method
Here, we only need to make two changes. First, change the salvage value from $30,000 to $60,000;
second, delete the line headed with “CCA tax shield”. Why delete this item? In the previous case when
S < UCC4, we lose S = $30,000 from the capital base, since this is how much you have recovered from
the sale of the old machine. In other words, the book value of capital investment at year 4 after selling
the old machine is $55,296 - $30,000 = $25,296. So, from year 5 and on, you only continue to enjoy tax
shields from this amount, which is the remaining book value of the capital cost. This is the base we used
to calculate the PV of all future CCA tax shields of $6,746.
Now, if the salvage value is $60,000, which is bigger than UCC4 = $55,296, you will recover all the book
value of capital investment. So you will not enjoy any future tax shields from CCA, since there is no CCA
to deduct anymore! That is why we don’t have that line “CCA tax shield” anymore. All you get from CCA
tax shields are the four numbers for each year under CCA*T: $4,800, $8,640, $6,912, and $5,530. In any
event, in this case, the time line method will lead to the following results:
0 1 2 3 4
Machine cost ($120,000)
NWC ($10,000)
CIF(1-T) $30,000 $30,000 $30,000 $30,000
CCA*T 4,800 8,640 6,912 5,530
Operating CF $34,800 $38,640 $36,912 $35,530
Salvage value $60,000
NWC recovery $10,000
Net CF ($130,000) $34,800 $38,640 $36,912 $105,530
PV of CF ($130,000) $31,636 $31,934 $27,733 $72,078
NPV $33,381
The formula Method
Everything is the same as before, except that S = $60,000 and UCC4 = $55,296, then you can double-
check that you get NPV = $33,381.