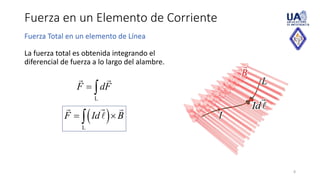
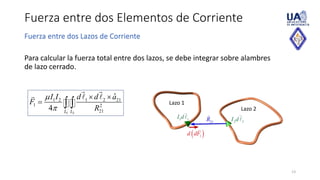
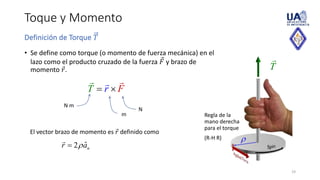
This document discusses forces on current-carrying elements in magnetostatics. It defines the magnetic force on a current element using the Lorentz force law. It then extends this to calculate the total force on linear and surface current distributions by integrating over the length or area. Expressions are also derived for the force between two current elements or loops by double integration. The concepts of magnetic torque, dipole moment, and dipole field are introduced for a current loop or dipole.

1. Tema 05:
Magnetostática
Campos Electromagnéticos, IEIE 62
Jorge Rabanal-Arabach, PhD
jorge.rabanal@uantof.cl

2. Esquema del Tema 05
Campos y corrientes
Fuerza de Lorentz
Fuerza sobre elementos con corriente
Condiciones de borde en magnetostática
Dispositivos magnetostáticos
2
5a
5b
5c
5d
5e

3. Fuerza en Elementos de
Corriente
Campos Electromagnéticos, IEIE 62
Jorge Rabanal-Arabach, PhD
jorge.rabanal@uantof.cl

4. Agenda
4
• Fuerza en un elemento de corriente.
• Fuerza entre dos elementos de corriente.
• Fuerza entre dos lazos de corriente.
• Toque magnético y momento.
• Dipolo magnético.

5. Fuerza en un Elemento de Corriente
5
Suponiendo que existe un elemento de corriente 𝐼𝑑ℓ

6. Fuerza en un Elemento de Corriente
6
Suponiendo que existe un elemento de corriente 𝐼𝑑ℓ
… aplicando un campo magnético 𝐵

7. Fuerza en un Elemento de Corriente
7
Suponiendo que existe un elemento de corriente 𝐼𝑑ℓ
… aplicando un campo magnético 𝐵
El campo magnético 𝐵 pone una fuerza 𝐹 en
el elemento de corriente 𝐼𝑑ℓ de acuerdo con
 
dF Id B
 

8. Fuerza en un Elemento de Corriente
8
La fuerza total es obtenida integrando el
diferencial de fuerza a lo largo del alambre.
 
L
F Id B
 

Fuerza Total en un elemento de Línea
L
F dF
 

9. Fuerza en un Elemento de Corriente
9
Recordando la expresión de la densidad de
corriente.
Entonces, la fuerza total en una corriente de
superficie es
 
S
F Kds B
 

Fuerza Total en un elemento de Superficie
Id Kds Jdv
 

10. Fuerza en un Elemento de Corriente
10
Recordando la expresión de la densidad de
corriente.
La fuerza total en una corriente volumétrica es
 
V
F Jdv B
 

Fuerza Total en un elemento de Superficie
Id Kds Jdv
 

11. La diferencial doble significa que se deberá
integrar sobre el largo de ambos alambres
para obtener la fuerza total.
Fuerza entre dos Elementos de Corriente
11
 
   
1 1 2 2 21
1 2
21
ˆ
4
I d I d a
d dF
R


 

Analogía con Ley de Coulomb en electrostática
  1 2 1 2 21
1 2
21
ˆ
4
I I d d a
d dF
R


 


12. Para calcular la fuerza total entre dos corriente de
línea, se debe integrar sobre el largo de cada
alambre.
Cada parte del segundo alambre pone una fuerza
en cada parte del primero.
Fuerza entre dos Elementos de Corriente
12
Fuerza entre dos Corrientes de Línea
1 2
1 2 1 2 21
1 2
21
ˆ
4 L L
I I d d a
F
R


 
  
 
1 2
1 1
L L
F d dF
  

13. Para calcular la fuerza total entre dos lazos, se debe integrar sobre alambres
de lazo cerrado.
Fuerza entre dos Elementos de Corriente
13
Fuerza entre dos Lazos de Corriente
1 2
1 2 1 2 21
1 2
21
ˆ
4 L L
I I d d a
F
R


 
   Lazo 1
Lazo 2

14. Escribiendo la integral para calcular la fuerza en el lazo 2
Comparando las ecuaciones para
𝐹1 y 𝐹2 se puede demostrar que
las fuerzas son iguales pero opuestas
Fuerza entre dos Elementos de Corriente
14
Fuerza entre dos Lazos de Corriente
2 1
2 1 2 1 12
2 2
12
ˆ
4 L L
I I d d a
F
R


 
  
Lazo 1
Lazo 2
2 1
F F
 

15. Toque y Momento
15
Fuerza en un Lazo (bucle) de Alambre
• Suponga un alambre que forma un lazo, y que porta una corriente 𝐼.

16. Toque y Momento
16
Fuerza en un Lazo (bucle) de Alambre
• Luego, aplicando un campo magnético 𝐵 orientado en el plano del lazo.
B

17. Toque y Momento
17
Fuerza en un Lazo (bucle) de Alambre
• Cada parte del alambre (lazo) percibirá una fuerza en direcciones distintas.
• Se puede demostrar que la fuerza neta sobre el lazo es cero, por lo que el lazo no se
traslada su posición.
B

18. Toque y Momento
18
Fuerza en un Lazo (bucle) de Alambre
• No obstante, la diferencia entre las fuerzas de ciertos extremos crean un torque sobre el
lazo que lo hará rotar.
• El lazo girará de forma tal que su sección transversal será perpendicular a 𝐵.
B

19. Toque y Momento
19
Definición de Torque 𝑇
• Se define como torque (o momento de fuerza mecánica) en el
lazo como el producto cruzado de la fuerza 𝐹 y brazo de
momento 𝑟.
r
T F
 
N m
m
N
T
El vector brazo de momento es 𝑟 definido como
ˆ
2 n
r a


Regla de la
mano derecha
para el torque
(R-H R)

20. Toque y Momento
20
Vector brazo de momento 𝑟
• Se define como
• La magnitud de 𝑟 es proporcional a cuan fácil el lazo puede ser rotado (girado).
• La dirección de 𝑟 es perpendicular a la sección cruzada del lazo.
B
ˆn
r wa


21. Toque y Momento
21
Momento Dipolar Magnético 𝑚
Es conveniente definir el momento dipolar magnético de forma tal que el torque en el lazo
pueda se calculado directamente del flujo magnético 𝐵
Para cualquier lazo plano,
Existe dependencia con el ángulo de alineamiento 𝛼
B
T m B
 
T
 
2
ˆ A m
n
m ISa

sin
T BIS 

Este parámetro agrupa todo sobre el lazo, para calcular
cómo responderá ante un campo magnético 𝐵.

22. Toque y Momento
22
Momento Dipolar Magnético 𝑚
 
2
ˆ A m
n
m ISa


23. Dipolo Magnético
23
Definición
Un dipolo magnético es un lazo cerrado de corriente eléctrica en el límite en
que el tamaño del lazo tendiente a cero.
El momento dipolar magnético para un
pequeño lazo de radio a es
 
2 2
ˆ A m
n
m a Ia



24. Dipolo Magnético
24
Definición
Campo magnético alrededor del dipolo (en coordenadas esféricas)
 
3
ˆ ˆ
2cos sin
4
r
m
B a a
r


 

 

25. Dipolo Magnético
25