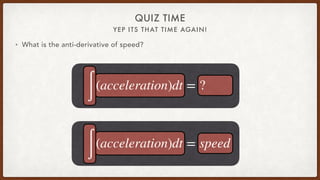
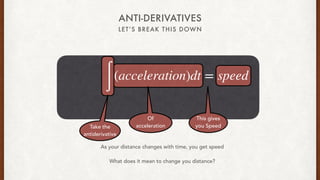
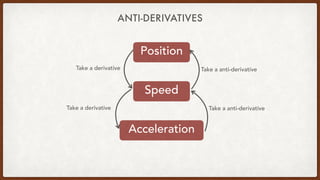
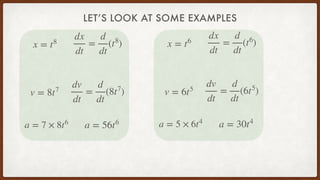The document discusses anti-derivatives and how they relate to derivatives. It provides examples of taking the anti-derivative of acceleration to find speed and discusses how anti-derivatives are like rewinding a function to find the original function. Examples are given of using the rule that if the number in front of t is one more than the power, you copy that number to the power when taking the anti-derivative. The document also discusses using models to represent real-world phenomena and provides a simple example model of drag car speed over time.

1. ANTI-DERIVATIVE TIME
CALCULUS

2. YEP ITS THAT TIME AGAIN!
QUIZ TIME
• What is the anti-derivative of speed?
∫
(acceleration)dt = ?
∫
(acceleration)dt = speed

3. LET’S LOOK AT SOME EXAMPLES
x = t8
dx
dt
=
d
dt
(t8
)
v = 8t7
dv
dt
=
d
dt
(8t7
)
a = 7 × 8t6
a = 56t6
x = t6
dx
dt
=
d
dt
(t6
)
v = 6t5
dv
dt
=
d
dt
(6t5
)
a = 5 × 6t4
a = 30t4

4. LET’S LOOK AT SOME EXAMPLES
x = t3
dx
dt
=
d
dt
(t3
)
v = 3t2
dv
dt
=
d
dt
(3t2
)
a = 2 × 3t a = 6t
x = t5
dx
dt
=
d
dt
(t5
)
v = 5t4
dv
dt
=
d
dt
(5t4
)
a = 4 × 5t3
a = 20t3

5. ANTI-DERIVATIVES

6. OK WHAT?
ANTI-DERIVATIVES
• So anti-derivatives are like starting at the end of a
movie and rewinding it to the beginning.
• With a derivative - you see how the function changes
over time
• With an anti-derivative - you’re given how the function
changes, but want the original function.

7. ANTI-DERIVATIVES
• So let’s look back at our position, velocity, acceleration examples.
• If I know the position, then, I can take the derivative to get _________?
• If I know the speed, then, I can take the derivative to get ___________?

8. ANTI-DERIVATIVES
• What if you only knew velocity?
• What if you only knew
acceleration?
• Well, that’s where anti-derivatives
come into help.
• We have to learn a few more
symbols and what they mean:)

9. LET’S BREAK THIS DOWN
ANTI-DERIVATIVES
Take the
derivative
Of speed
This gives you
acceleration
As your distance changes with time, you get speed
What does it mean to change you distance?
d
dt
(speed) = acceleration

10. LET’S BREAK THIS DOWN
ANTI-DERIVATIVES
Take the
antiderivative
Of
acceleration
This gives
you Speed
As your distance changes with time, you get speed
What does it mean to change you distance?
∫
(acceleration) = speed

11. LET’S BREAK THIS DOWN
ANTI-DERIVATIVES
Take the
antiderivative
Of
acceleration
This gives
you Speed
As your distance changes with time, you get speed
What does it mean to change you distance?
∫
(acceleration)dt = speed

12. LET’S BREAK THIS DOWN
ANTI-DERIVATIVES
Take the
antiderivative
Of
acceleration
This gives
you Speed
As your distance changes with time, you get speed
What does it mean to change you distance?
∫
(speed)dt = position

13. Acceleration
ANTI-DERIVATIVES
Position
Speed
Take a derivative
Take a derivative Take a anti-derivative
Take a anti-derivative

14. LET’S LOOK AT A FEW EXAMPLES OF WHAT THE ANTI-DERIVATIVE LOOKS LIKE
ANTI-DERIVATIVE EXAMPLES
∫
6tdt
∫
2tdt
∫
3t2
dt
∫
(speed)dt
∫
5t6
dt
∫
7t8
dt
Remember, the dt at the end is just something we put there!
It doesn’t really do anything.

15. 3 is one more than 2.
We can take the anti-
derivative!
∫
3t2
dt
One rule - if the number in front of the
t is one more than the power
Then - copy and paste the number in
front of the t and paste it in the power
(up top and to the right of the t)

16. 4 is one more than 3.
We can take the anti-
derivative!
∫
4t3
dt
One rule - if the number in front of the
t is one more than the power
Then - copy and paste the number in
front of the t and paste it in the power
(up top and to the right of the t)

17. 2 is NOT one more
than 5. We cannot
take the anti-
derivative!
∫
2t5
dt
One rule - if the number in front of the
t is one more than the power
Then - copy and paste the number in
front of the t and paste it in the power
(up top and to the right of the t)

18. HOW TO FIND THE ANTI-DERIVATIVE
ANTI-DERIVATIVE EXAMPLES
∫
2tdt = t2
Remember, the dt at the end is just something we put there!
It doesn’t really do anything.
∫
3t2
dt = t3
∫
300t299
dt = t300
One rule - if the number in front of the
t is one more than the power
Then - copy and paste the number in
front of the t and paste it in the power
(up top and to the right of the t)

19. HOW TO FIND THE ANTI-DERIVATIVE
ANTI-DERIVATIVE EXAMPLES
∫
7t6
dt = t7
Remember, the dt at the end is just something we put there!
It doesn’t really do anything.
∫
3t2
dt = t3
∫
2t5
dt = Can′t do this yet!
One rule - if the number in front of the
t is one more than the power
Then - copy and paste the number in
front of the t and paste it in the power
(up top and to the right of the t)

20. LET’S CHANGE GEARS HEAR
• What does it mean when someone says “Theoretical”
• Yes, it just means the idea is all based in math!
• What does it mean when someone what’s to create a
scientific model?
• In science, a model is a representation of an idea, an even
a process that is used to describe and explain phenomena
that cannot be experienced directly.
• Models are central to what scientists do, both in their
research as well as when communicating their
explanations.
• Models have a variety of uses – from providing a way of
explaining complex data to presenting as a hypothesis.

21. LET’S BUILD A MODEL
• Well, you guys and girls have
been doing this all along.
• Let’s say we want to model the
speed of a drag car.
• Let’s go!
• What do we need to build the
model?
• We will start with an equation

22. MODEL BUILDING
•
• This is the equation that describes a drag car moving from the start line to the finish line.
• We want to know the velocity at 4 minutes after beginning of the race.
•
•
•
x = t2
dx
dt
=
d
dt
(t2
)
speed = 2t
speed = 2 × 4 = 8
(
ft
min)

23. WHAT’S WRONG WITH OUR MODEL?
• Whats missing from our model of a real world drag race car speed?
• What about the wind?
• Little bitty accelerations?
• The weight of the car?
• The friction made with the ground and tires?
• The drag race car is not going in a perfectly straight line?

24. SO WHY DO WE EVEN MAKE MODELS
• We can create scientific models from
calculus
• The models are a simple explanation
of something very complicated
• However, it is close to the real thing
to be “good enough”
• Then, we can use calculus and
something called statistics to see
“how good” a model is?