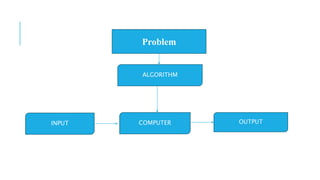
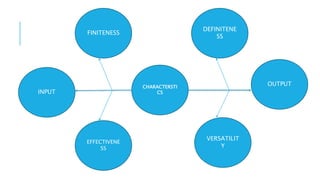
The document discusses algorithms, defining them as unambiguous sequences of instructions that solve problems and produce outputs based on given inputs. It highlights key characteristics of algorithms such as finiteness, definiteness, effectiveness, and flexibility, alongside the importance of time and space efficiency. The analysis of specific algorithms, like Euclid's for finding the greatest common divisor (GCD), demonstrates how algorithm efficiency can be evaluated through time and space complexity.

1. DESIGN AND ALGORITHM IV SEMESTER

2. ALGORITHM
An algorithm is a sequence of
unambiguous instructions for solving a
problem i.e., for obtaining required
output for any legitimate input in a
finite amount of time.

3. EXAMPLES
Daily Life-Preparing meal
GPS Navigation-calculate best route for the location
Finance Industry-Pricing, timing and volume of stocks
Health care Industry-diagnosing diseases
Computer Science-Image recognition, sorting data in database

4. NOTION OF THE ALGORITHM
The unambiguous instruction for solving a problem.
The range of inputs for which an algorithm work has to be specified carefully.
The same algorithm can be represented in several different ways.
There may exist several algorithms to solve the same problem.
Algorithms for the same problems can be based on very different ideas and solve the
problem dramatically different speed.

5. Problem
ALGORITHM
OUTPUT
COMPUTER
INPUT

6. CHARACTERSTICS OF ALGORITHM
Finiteness:-An algorithm must always terminate after number of steps.
 Example: Sum of all numbers the numbers in the list
Definiteness:-Each steps should be unambigious an clearly defined.
 Example:-Algorithm to prepare coffee
Input:-Algorithm should be abled to accept zero or more inputs to operate on the input to produce proper
output
 Example:-GPS Navigation
Output:-Algorithms should produce one or more outputs
 Example:-GPS Navigation
Effectiveness:-Operations should be conducted in finite number of steps.
 Example:-Sort list of numbers in ascending order
Versatility or Flexibility:-It represents the capacity of an algorithm to solve single problem by different
algorithm techniques.
 Example:-Searching an element in an array list.

7. CHARACTERSTI
CS
DEFINITENE
SS
EFFECTIVENE
SS
INPUT
FINITENESS
OUTPUT
VERSATILIT
Y

8. NEED FOR DDA
Effective ways to solve the computational problems and evaluate their performance.
Emphasizes for problem solving and also optimizing the solution for maximum
efficiency.
Time efficiency:-How fast algorithm executes
Space efficiency:-How much memory the algorithm uses

9. CONTD…
Design of Algorithms
It requires deep understanding of the problem domain.
It may involve design strategies.
 Ex: creating guest list for a party
Analysis of Algorithms
Analyse to determine its efficiency and effectiveness.
Perform in terms of time and space complexity.
Time Complexity: computational time to solve the algorithm
Space complexity: The memory used during computation.
Ideal Algorithm is one that achieves the desired result with minimal time and space
usage.

10. EXAMPLE OF GCD
GCD OF TWO NON NEGATIVE AND
NON-ZERO INTEGERS

11. EUCLID’S ALGORITHM
GCD(m,n)= GCD(n,m) if n>m
m if n=0
GCD(n,MOD(m,n)) otherwise

12. FIND GCD(288,108)
=GCD(108,MOD(288,108))
=GCD(108,72)
GCD(108,72)=GCD(108,MOD(108,72))
=GCD(72,36)
GCD(72,36)=GCD(72,MOD(72,36))
=GCD(36,0)=36
288/108=2.6667
108*2=216
REMINDER=288-216=72
108/72=1.5
72*1=72
REMINDER=108-72=36
72/36=2
REMINDER=0

13. EUCLID’S ALGORITHM FROM
COMPUTING GCD(m,n)
Step 1:check for second equality to be non-zero i.e, if
n=0, return the value of ‘m’
And stop. otherwise go to step 2.
Step 2:Calculate MOD(m,n) and assign this value to be a
temporary variable ‘t’.
Step 3:Assign the value of ‘n’ to ‘m’ and ‘t’ to ‘n’. Go to
step1

14. CONSECUTIVE INTEGER CHECKING
ALGORITHM
Step 1:Assign the value of min{m,n} to t
Step 2:Calculate MOD(m,t).If it is zero, go to Step 3, else go to Step 4.
Step 3:Calculate MOD(n,t).If it is “zero”, return the value of ‘t’ as answer and stop,
else go to step 4
Step 4:Decrement ‘t’ by 1 and go to step 2.

15. PSUEDO CODE
// Input:Two non-negative, non zero integers m,n
//Output:Greatest common divisor of m,n
{
while n=/0 do
{
t=m mod n
m=n
n=t
}
return m
}

16. ANALYSIS OF EUCLID’S
ALGORITHM
1. Euclid’s Algorithm is an iterative process.
2. Algorithm reduces the problem of finding GCD of two large numbers to smaller
numbers.
3. The time taken to solve the problem is quick and efficient than other methods.
LIMITATIONS:
BOTH THE INPUTS SHOULD BE POSITIVE

17. FIND GCD(8,6)
//computing the GCD(m,n)
//Input:Two non-negative, not both zero integers m,n.
/Output:Greatest common divisor of m,n.
T=min(m,n)
While(t=/0) do
{
t=m mod t
if(t=0)
{
t=n mod t
if(t==0)
{
return t
}
}
t=t-1
}

18. S1: Smaller 8 and 6 assign the value of 6.(t=6)
S2:8/6=non zero reminder,so move to s4
S4:t decresead by 1, changing its value from 6 to 5.Go to S2.
S2:8/5=non zero reminder, move on to s4.
S4:t is decreased by 1, changing its value from 5 to 4.Go to S2
S2:8/4=leaves reminder 0, move to S3.
S3:6/4= leaves non zero reminder, so we move to s4
S4:t is then decreased by 1, changing its value from 4 to 3.Go to S2.
S2:8/3= non zero, move to s4
S4:t decreased by 1, changing its value from 3 to 3.Go to Step 2.
S2:8/2=non zero reminder, move to s3
S3:6/2 reminder =0, the value of t becomes the GCD 8 and 6 =2

19. ANALYSIS OF CICA
1. Checks each integer one at a time to see if it
divides both m and n without leaving a reminder
2. Many Checks are redundant
3. Inefficient for large numbers

20. PROBLEMS TYPES

21. PROBLEM TYPES
Sorting
Searching
String Processing
Combinational Problems
Graphs Problems
Combinational Problems
Geometric Problems
Numerical Problems

22. FUNDAMENTAL DATA
STRUCTURE
Primitive Data structure
int, real, character, Boolean
Non-Primitive Data structure
 Linear:- array, linked list, stack, queue
Non-Linear:- Trees, Graphs

24. STEP COUNT
In step count method, we attempt to find the time spent in all parts of the program.
A step is any computational unit that is independent of the selected characteristics.

25. EXAMPLE FOR STEP COUNT
:FINDING SUM OF ALL ARRAY
ELEMENTS
int sum(int a[],int n)
{
int i, sum=0;
for (i=0;i<n;i++)
{
sum=sum+a[i];
}
return sum
}
Step count
sum=1
for=n+1
assignment of sum = n
Return =1
Consider each statement rather
than basic operations.

26. STEPS PER EXECUTION
Here we build a table in which we list the total number of steps contributed
by each statement.
We determine the number of steps per execution(S/E) of the statement and
total number of time( frequency) each statement is executed

27. Statement S/E Frequency Total Steps
1.Algorithm
sum(x,n)
0 0 0
2.{ 0 0 0
3.Total =0.0; 1 1 1
4.For i=0 to n
do
1 n+1 n+1
5.Total=Total+
x[i]
1 n n
6.Return Total; 1 1 1
7.} 0 0 0
Total Steps (2n+3)

28. CONTD..
The total number of steps required by the algorithm is (2n+3)
It is important to see that frequency of the ‘for’ statement is (n+1), since i is to be
incremented to (n+1) before the for loop can terminate

29. ALGORITHM EFFICIENCY
MEASURED
Efficiency is measured by the complexity function T(n) and n indicating the size of
the algorithm’s input.
When analysing the performance of algorithms, we often consider 3 different cases:
 Worst Case: It gives the maximum value of T(n) for any possible input
 Best Case: It gives the minimum value T(n) for any possible input
 Average case: It gives the expected value of T(n) for any possible input
 Complexity of average of an algorithm is usually much more complicated to
analyse. In some cases, it may require complex mathematical analysis or
statistical knowledge to calculate

30. WORST CASE EFFICIENCY
Maximum amount of time an algorithm takes to complete its task.
It helps to understand the upper bound on the time complexity of an algorithm.
It is denoted by Tworst(n)
It represents the maximum amount of time an algorithm, takes for any input size n.
It determines the worst-case efficiency of an algorithm
It is analysed by giving the kind of inputs makes the algorithm to run longest.
Ex:Linear search algorithm : for an unsorted array and when the element is not present
in the array

31. BEST CASE EFFICIENCY
It refers to the minimum amount of time an algorithm takes to complete its task.
It is important to consider this case because it helps us understand the lower bound
on the time complexity of the algorithm.
It is denoted by Tbest(n)
It represents the minimum amount of time an algorithm takes for any input size n.
To determine the best-case effieciency of an algorithm, the run fastest type of input
should be used.
Example:Binary search: Element present in the mid of the sorted array
No. comparision=1 i.e, o(1) regardless of inut size of n

32. AVERAGE CASE EFFICIENCY
It refers to how long an algorithm takes on average over all possible inputs.
it helps us understand how well an algorithm perform in practice.
It is denoted by Tavg(n)
It represents how long an algorithm takes on average for any input size n.
Analysed by the possible inputs.
Example:Quick sort:it divides the array to subarray the sort and merges together
Average case:O(n log n) : it takes n log n comparisons and swaps to sort an array