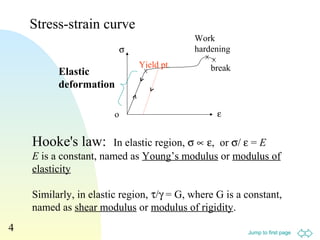
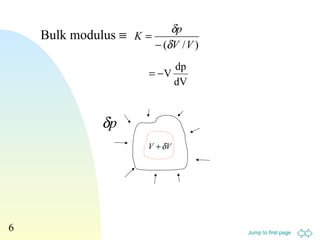
1. The document discusses concepts in mechanics of materials including stress, strain, elastic deformation, stress-strain curves, shear stress, normal stress, Poisson's ratio, and elastic strain energy. 2. Various equations are presented for calculating stress, strain, elastic moduli like Young's modulus, shear modulus, and bulk modulus. 3. Examples are provided to demonstrate relationships between stress and strain components, normal and shear strains, and derivation of equations for elastic moduli.

1. Jump to first page
1
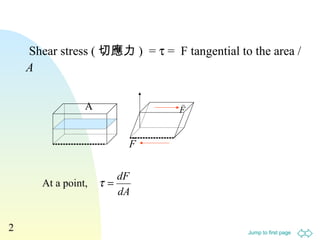
dA
dF
A
F
A
==
→ δ
δ
σ
δ 0
lim
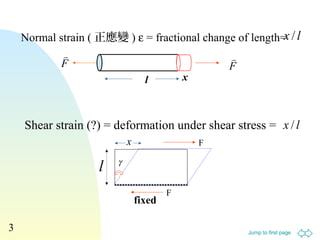
Normal stress = [ ] )Pa(pascalm/N
A
Force 2
≡σ
Chapter 2 Mechanics of Materials
Example: Estimate the normal stress on a shin bone ( 脛骨
)
AF

F

F

F
 F

F
 Tensile stress (+)
F

F

Compressive stress (-)
At a point:

2. Jump to first page
2
Shear stress ( 切應力 ) = τ = F tangential to the area /
A
A F

F

dA
dF
=τAt a point,

3. Jump to first page
3
Normal strain ( 正應變 ) ε = fractional change of length= lx /
x
l γ
F
F
fixed
lx /Shear strain (?) = deformation under shear stress =
F

F

l x

4. Jump to first page
4
Stress-strain curve
σ
εo
Yield pt.
Work
hardening
breakElastic
deformation
Hooke's law: In elastic region, σ ∝ ε, or σ/ ε = E
E is a constant, named as Young’s modulus or modulus of
elasticity
Similarly, in elastic region, τ/γ = G, where G is a constant,
named as shear modulus or modulus of rigidity.

5. Jump to first page
5
Exercise set 2 (Problem 3)
Find the total
extension of the bar.
dx
x
dxde 2
4
1092.1 −
×=ε=
)(
120
)105(
6.0
3
mxm
m
xW =×= −
Pa
xmx
N
2
7
22
3
1088.2
)120/(
102 ×
=
×
=σ
X
15mm
W5mm
1.2m0.6m
o
kN2
dx
2
4
9
27
1092.1
10150
/1088.2
x
x
E
−
×
=
×
×
==
σ
ε
Width of a cross-sectional element at x:
Stress in this element :
Strain of this element:
The extension of this element :
The total extension of the whole bar is :
= 2.13 x 10-4
m
∫ ∫
−
×
==
8.1
6.0 2
4
1092.1
dx
x
dee

6. Jump to first page
6
Bulk modulus ≡
)/( VV
p
K
δ
δ
−
=
VV δ+
pδ
dV
dp
V−=

7. Jump to first page
7
Poisson's ratio :
For a homogeneous isotropic material
normal strain :
lateral strain :
Poisson's ratio :
value of ν : 0.2 - 0.5
d
d
L
∆
=ε
εεν /L−≡

x
=ε
F F

dd ∆+
x
d

8. Jump to first page
8
Double index notation for stress and strain
1st
index: surface, 2nd
index: force
For normal stress components : x ⇒ xx, y ⇒ yy , z ⇒ zz,
σx ⇒ σxx
zσ
xσ
yσ
x
y
z
σzx
σzy
σyz
σxz
σxy
σyx

9. Jump to first page
9
EEE
EEE
EEE
yyxxzz
zz
zzxxyy
yy
zzyyxx
xx
νσ
−
νσ
−
σ
=ε
νσ
−
νσ
−
σ
=ε
νσ
−
νσ
−
σ
=ε
zσ
xσ
yσ
x
y
z
Joint effect of three normal stress components

10. Jump to first page
10
Symmetry of shear stress components
Take moment about the z axis, total torque = 0,
(σxy ∆y∆z) ∆x = (σyx ∆x ∆z) ∆y, hence, σxy = σyx .
Similarly, σyz = σzy and σxz = σzx
z
y
x
σxy
σyx
∆x
∆y
∆z

11. Jump to first page
11
Define pure rotation angle θrot and
pure shear strain, such that the angular
displacements of the two surfaces are:
γ1= θrot+ θdef and γ2= θrot- θdef . Hence,
θrot = (γ1+ γ2)/2 and θdef = (γ1- γ2)/2
Original shear strain is “simple” strain = etc.,...,
y
dx
x
dy
∆∆
There is no real deformation during pure rotation,
but “simple” strain ≠ 0.
x
y
∆x
γ2 = -γ
Example: γ1 = 0 and γ2 = - γ,
so θdef = (0+γ)/2 = γ/2 and θrot= (0-γ)/2 = -γ/2
Pure shear strain is γ/2
x
y
∆x
dy1γ θrot
γ2
θdef
θdef

12. Jump to first page
12
Example: Show that
)21(3 ν−
=
E
K
)21(3
E
V/V
p
K
ν−
=
∆
∆
−≡∴
3
33)(
l
lll
V
V −∆+
=
∆
ε3/3 =∆≅ ll
Proof:
εxx = εyy = εzz = ε, hence
3ε = εxx+εyy+εzz = (1-2v)(σxx+σyy+σzz)/E
σxx =σyy =σzz = -∆p (compressive stress)
)(
)21(
3 p
E
∆−
ν−
=
V
V∆
For hydrostatic pressure
l
l
l

13. Jump to first page
13
Point C moves further along x- and y-direction by distances
of AD(γ/2) and AD(γ/2) respectively.
εnn = [(AD . γ/2)2
+ (AD . γ/2)2
]1/2
/ [(AD)2
+ (AD)2
]1/2
= γ/2
True shear strain: εyx = γ/2
Therefore, the normal component of strain is equal to the
shear component of strain:
εnn = εyx and εnn = γ/2
Example : Show that εnn = γ/2
2/γ x
y
A
C’
C
D
D’2
γ

14. Jump to first page
14
σ yx (lW) sin 45o
x2 = 2 (l cos 45o
) W σnn
Example : Show that εnn = σnn/(2G)
Consider equilibrium along n-direction:
Therefore σyx = σnn
From definition : γ = σxy /G = σnn /G = 2 εnn
l
l
σn
σyx
σxy
2
lcos45
o

15. Jump to first page
15
G
v
E
2
1
=
+
∴
σnn
σnn
-σnn
-σnn
εxx = σxx/E - ν σyy/E- v σzz/E
Set σxx = σ nn = -σ yy, σ zz = 0, εxx = εnn
εnn = (1+ν) σ nn /E = σ nn /2G (previous example)
Example : Show G
v
E 2
1
=
+

16. Jump to first page
16
Ex. 12 kN forces are applied to the top
& bottom of a cube (20 mm edges), E =
60 GPa, ν = 0.3. Find (i) the force
exerted by the walls, (ii) εyy
z
y
12kN
x
(ι) εxx = 0, σyy = 0 and
σzz= -12×103
N/(20×10-3
m)2
= 3×107
Pa
εxx = (σxx- v σyy- v σzz) /E
0 = [σxx- 0 – 0.3×(- 3×107
)]/60×109
∴ σxx = -9×106
Pa (compressive)
Force = Aσxx = (20×10-3
m)2
×(-9×106
Pa) = -3.6 ×103
N
(ii) εyy = (σyy- v σzz- v σxx) /E
= [0 – 0.3×(- 3×107
) – 0.3×(- 9×106
)]/60×109
= 1.95×10-4

17. Jump to first page
17
Elastic Strain Energy
The energy stored in a small volume:
∴ The energy stored :
∴ Energy density in the material :
dx
x
AEFdxdU )(

==
VE
A
e
E
AEe
dxx
AE
U
e
⋅=
==
= ∫
2
2
2
0
2
1
)()(
2
1
2
1
)(
ε



E
E
V
U
u
2
2
2
1
2
1 σ
ε ==≡
e=extension
dx
F F

x

18. Jump to first page
18
Similarly for shear strain :
F
dx

∫ ⋅= xdFU

∫= Fdx
γ
τ
==
/
/
x
AF
G
G
Gu
2
2
2
1
2
1 τ
γ ==∴