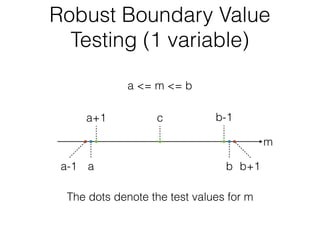
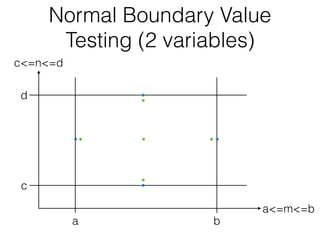
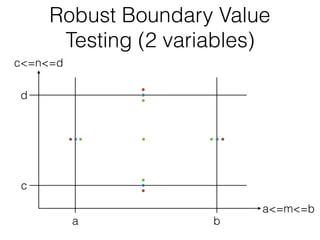
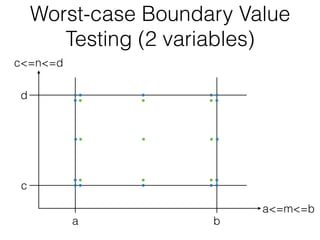
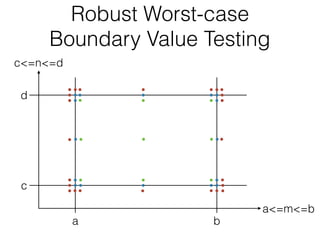
The document discusses boundary value testing, focusing on both normal and robust variants for one and two variables, outlining test cases within and at limits, as well as beyond limits. It highlights the differences between normal boundary value testing, which assumes single-fault conditions, and worst-case boundary value testing, which does not. Additionally, it notes limitations such as not accounting for variable interactions and potential oversaturation of tests in worst-case scenarios.

1. Boundary Value
Testing
Venkatesh-Prasad Ranganath
Kansas State University

2. Normal Boundary Value
Testing (1 variable)
a <= m <= b
b-1
a b
a+1 c
m
The dots denote the test values for m

3. Normal Boundary Value
Testing (1 variable)
Given a <= m <= b,
• Test cases within limits
• m == a+1
• m == c (a < c < b)
• m == b-1
• Test cases at limits
• m == a
• m == b

4. Robust Boundary Value
Testing (1 variable)
b-1
a <= m <= b
a b
a+1 c
a-1 b+1
m
The dots denote the test values for m

5. Robust Boundary Value
Testing (1 variable)
Given a <= m <= b,
• Test cases within limits
• m == a+1
• m == c (a < c < b)
• m == b-1
• Test cases at limits
• m == a
• m == b
• Test case beyond limits
• m == a-1
• m == b+1

6. a<=m<=b
c<=n<=d
d
c
a b
Normal Boundary Value
Testing (2 variables)

7. d
c
a b
Robust Boundary Value
Testing (2 variables)
a<=m<=b
c<=n<=d

8. Worst-case Boundary Value
Testing (2 variables)
d
c
a b
a<=m<=b
c<=n<=d

9. Robust Worst-case
Boundary Value Testing
d
c
a b
a<=m<=b
c<=n<=d

10. Boundary Value Testing
• Normal boundary value testing (including robust
variant) relies on the single-fault assumption
• failures are rarely the result of the simultaneous
occurrence of two (or more) faults
• To generate test cases, while holding all variables
at a valid value, consider valid and boundary
values for a variable
• 4n+1 (6n+1) test cases result from normal (robust)
boundary value testing where n is the number of
variables

11. Boundary Value Testing
• Worst-case boundary value testing (including
robust variant) does not rely on the single-fault
assumption
• failures can result from simultaneous
occurrences of two (or more) faults
• To generate test cases, consider all combinations
of valid and boundary values for all variables
• 5n (7n) test cases result from worst-case (robust
worst-case) boundary value testing where n is the
number of variables

12. Limitations
• Does not consider the interactions of variables
(redundancy)
• May miss out on interesting parts of value ranges
(completeness)
• What about the specifications that do not
describe the output for invalid input?
• Too many tests in worst-case variants
• Works well with data types for which boundaries
can be well-defined.