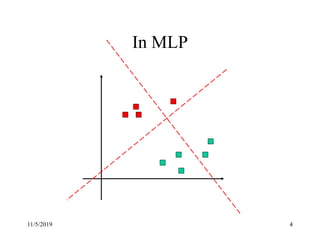
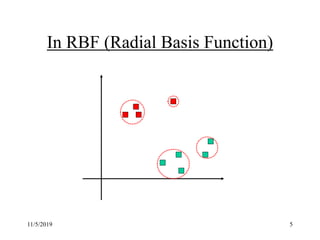
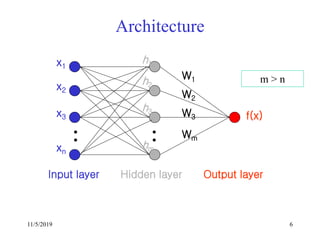
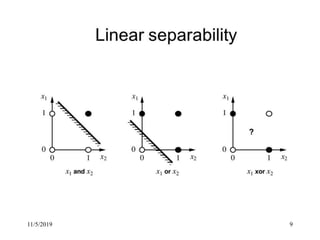
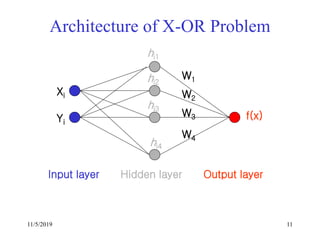
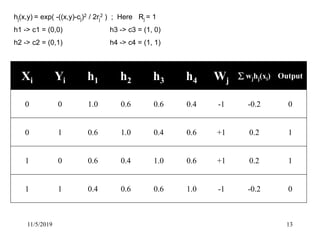
This document discusses radial basis functions and splines for neural network modeling. It presents the architecture of a radial basis function network, which uses radial basis functions as activations in a single hidden layer. The network approximates functions as a linear combination of radial basis functions centered at different locations. The document then shows how to classify the output of an XOR gate using such a network with 4 radial basis functions in the hidden layer and computes the weights between the hidden and output layers to perform the classification.

1. 11/5/2019 1
Radial Basis Functions and Splines
Presented by…
Bikash Baruah
PhD(CSE)/2019/04

2. 11/5/2019 2
Contents
• Introduction
• Architecture
• Designing
• Learning strategies

3. 11/5/2019 3
Introduction
• The design of a neural network using Radial Basis Function
is a curve-fitting (approximation) problem in high-
dimensional space.
• Unlike Multilayer Perceptron it can have Single Hidden
Layer.

4. 11/5/2019 4
In MLP

5. 11/5/2019 5
In RBF (Radial Basis Function)

6. 11/5/2019 6
Architecture
Input layer Hidden layer Output layer
x1
x2
x3
xn
h1
h2
h3
hm
f(x)
W1
W2
W3
Wm
m > n

7. 11/5/2019 7
Radial Basis Function Network
• Approximate function with linear combination of
Radial basis functions
F(x) = S wi h(x)
• h(x) is mostly Gaussian function

8. 11/5/2019 8
Three layers
• Input layer
– Source nodes that connect to the network to its
environment / hidden layer.
• Hidden layer
– Hidden units provide a set of basis function
– High dimensionality
• Output layer
– Linear combination of hidden functions

9. 11/5/2019 9

10. Q. Classify the output of two input EX-OR
gate using Radial Basis Function and Splines.
11/5/2019 10

11. 11/5/2019 11
Architecture of X-OR Problem
Input layer Hidden layer Output layer
hi1
hi2
hi3
hi4
f(x)
W1
W2
W3
W4
Yi
Xi

12. 11/5/2019 12
Radial basis function
hj(x) = exp( -(x-cj)2 / 2rj
2 )
f(x) =  wjhj(x)
j=1
m
Where cj is center of a region,
rj is Nearest Neighbor Distance

13. Xi Yi h1 h2 h3 h4 Wj
 wjhj(xi) Output
0 0 1.0 0.6 0.6 0.4 -1 -0.2 0
0 1 0.6 1.0 0.4 0.6 +1 0.2 1
1 0 0.6 0.4 1.0 0.6 +1 0.2 1
1 1 0.4 0.6 0.6 1.0 -1 -0.2 0
11/5/2019 13
hj(x,y) = exp( -((x,y)-cj)2 / 2rj
2 ) ; Here Rj = 1
h1 -> c1 = (0,0) h3 -> c3 = (1, 0)
h2 -> c2 = (0,1) h4 -> c4 = (1, 1)

14. 11/5/2019 14
Computation of Weight (Wj)
f(x) =  wjhj(x)
(i) Now, Calculate the Error
 e =  wjhj(x) – f(x)
(ii) If Error is present
Use Gradient function
 wj = [hj
T hj]-1 hj f(x)
(iii) If input € wj
then f(x) = 1
else
f(x) = 0
h1 h2 h3 h4
1.0 0.6 0.6 0.4
0.6 1.0 0.4 0.6
0.6 0.4 1.0 0.6
0.4 0.6 0.6 1.0
The Value of hj

15. 11/5/2019 15
Assignment
• Classify the output of two input EX-OR gate using Radial
Basis Function and Splines.

16. Thank You…
11/5/2019 16