This document contains a multiple choice quiz on statistics concepts. The quiz covers topics like descriptive statistics, populations, sampling, data collection and classification. Some key points covered are:
- Descriptive statistics are used to summarize or describe data
- Inferential statistics are needed due to sampling from populations
- A population is the total set being studied, defined by its variables
- Samples are used to make inferences about populations
- Data classification includes grouping data by time, location, characteristics and other attributes





































![39
c) f(1) = 1/19 , f(2) = 10/19 , f(3) = 2/19 , f(4) = 5/19
d) None of these
15. For what values of k can f(x) = (1-k) kx
a) 0k1
b) k=0
c) k1
d) None of these
16. From a bag containing 4 white and 6 red balls, three balls are drawn at random and if each
white ball drawn carries a reward of Rs4 and each red ball Rs6, find the expected reward of the
draw
a) Rs14.8
b) Rs15.6
c) Rs31
d) Rs16
17. A lot of 12 television sets include 2 with white chords. If 3 of the sets are chosen at random
for shipment to the hotel, how many sets with white chords can the shipper expect to send to the
hotel
a) 0
b) 1
c) 1/2
d) All of the above
18. The joint probability density function
f(x,y) = 3/5x(y+x) for 0x1 0y2
0 elsewhere
Of 2 random variables X and Y, find P[(X,Y)€A] where A is the region (x,y)/0 x, ½, 1y2
a) 11/65
b) 11/80
c) 10/76
d) 67/80
19. E(x2) = 91/6. Find the value of E(2 x2+1) is
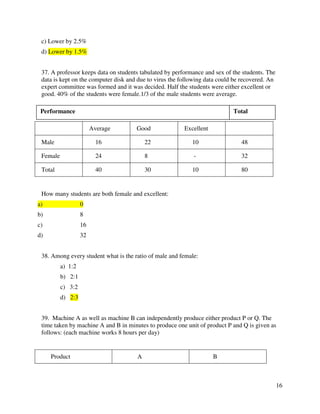
a) 92/3
b) 91/3](https://image.slidesharecdn.com/bcabusinessstatistics-141118083714-conversion-gate01/85/Bca-business-statistics-39-320.jpg)
![40
c) 90/3
d) 94/3
20. If the probability density of X is given by
f(x) = 2(1-x) for 0x1
0 elsewhere
To evaluate E[(2X+1)2]
a) 2
b) 1
c) 4
d) 3
21. If X has the probability density
f(x) = ex for x0
0 elsewhere
Find the expected value of g(X) = e3x/4
a) 1
b) 2
c) 3
d) 4
22. Given that X has the probability distribution f(x) = 1/8(3/x) for x = 0, 1, 2 and 3, find the
moment-generating function of this random variable and use it to determine μ1`and μ2 `
a) 0
b) 3/2
c) 1/2
d) 1
23. For any random variable for which E(x) exists find the value of μ0
a) 0
b) -1
c) 2
d) 1](https://image.slidesharecdn.com/bcabusinessstatistics-141118083714-conversion-gate01/85/Bca-business-statistics-40-320.jpg)



