This document provides an introduction to Bayesian regression. It describes using a Bayesian approach to analyze a dataset on bird extinction times using multiple linear regression. Key steps include specifying prior distributions, computing the joint posterior distribution of the regression coefficients and error variance, and using MCMC methods like the blinreg() function to simulate values from the posterior. Graphical results show the distributions of coefficients and model predictions for different covariate patterns.

1. Bayesian Regression
An Introduction Using R
J Guzmán, PhD
January 2011

2. Multiple Regression
• Model:
µ|X,β = β0 + β1x1 + … + βkxk
y | X,β = β0 + β1x1 + … + βkxk + ε
ε ~ N(0, σ2)
• k predictors or explanatory variables
• n observations

3. Multiple Regression
• Matrix notation:
y |β,σ2, X ~ N(Xβ, σ2I)
• X matrix of explanatory variables
• β vector of regression coefficients
• y response or variable of interest
vector
• ε vector of normally distributed random
errors

4. Example: Birds’ Extinction
• Albert, 2009. Bayesian Computation with R,
2d. Edition. Springer.
• Birds’ extinction – data from 16 islands
• species – name of bird species
• time – average time of extinction on the
islands
• nesting – average number of nesting pairs
• size – species’ size, 1 = large; 0 = small
• status – species’ status; 1 = resident,
0 = migrant

5. Example
library(LearnBayes)
data(birdextinct)
attach(birdextinct)
birdextinct[1:15, ]

6. Linear Model
• Graphical display:
log.time = log(time)
plot(log.time ~ nesting)
• Linear Model
t.lm = lm(log.time ~ nesting +
size + status, x = T, y = T )
summary(t.lm)

7. Birds’ Extinction
• From output:
a. longer extinction times for species with
large no. of nesting pairs
b. smaller extinction times for large birds
c. longer extinction times for resident birds

8. Bayesian Regression
• Model: y | β, σ2, X ~ N(Xβ, σ2I)
• Two unknown parameters: β & σ2
• Assume un-informative joint prior:
f(β, σ2) ∝ 1/σ2
• Joint posterior:
f(β, σ2 | y) ∝ f(β | y, σ2) × f(σ2 | y)

9. Bayesian Regression
• Marginal posterior distribution of β,
conditional on error variance σ2 is
Multivariate Normal with:
Mean = b = (XtX)-1Xty
var(β) = σ2 ⋅ (XtX)-1
• Marginal posterior distribution of σ2 is
Inverse Gamma[(n - k)/2, S/2]
S = (y - Xb)t (y - Xb)

10. Prediction
• To predict future yp , based on vector xp
• Conditional on β & σ2, yp ~ N(xpβ, σ2)
• Posterior predictive distribution
f(yp|y) = ∫f(yp|β, σ2)f(β, σ2|y)dβdσ2

11. Computation
• Simulate from joint posterior of β & σ2:
– Simulate value of σ2 from f(σ2| y)
– Simulate value of β from f(β | y, σ2)
• Use Albert’s blinreg( ) to perform
simulation
• To predict mean response µy use
Albert’s blinregexpected( )
• To predict future response yp use
Albert’s blinregpred( )

12. blinreg( )
• To sample from joint posterior of β & σ2
• Inputs: y, X & no. of simulations m
par.sample = blinreg(t.lm$y, t.lm$x,
5000)
S = sum(t.lm$residuals^2)
shape=t.lm$df.residual/2; rate = S/2
library(MCMCpack)
sigma2 = rinvgamma(1, shape, scale =
1/rate)

13. Computation
• β is simulated from Multivariate
Normal:
Mean = b = (XtX)-1Xty
var(β) = σ2 ⋅ (XtX)-1
MSE = sum(t.lm$residuals^2)/ t.lm
$df.residual
vbeta = vcov(t.lm)/MSE
beta = rmnorm(1, t.lm$coef,
vbeta*sigma2)

14. Graphical Display
op = par(mfrow = c(2,2))
hist(par.sample$beta[, 2],
main= "Nesting",
xlab=expression(beta[1]))
hist(par.sample$beta[, 3],
main= "Size",
xlab=expression(beta[2]))

15. Graphical Display
hist(par.sample$beta[, 4],
main= "Status",
xlab = expression(beta[3]))
hist(par.sample$sigma,
main= "Error SD",
xlab=expression(sigma))
par(op)

16. Parameters’ Summary
• Compute 2.5th , 50th & 97.5th percentiles
apply(par.sample$beta, 2,
quantile, c(.025, .5, .975))
quantile(par.sample$sigma,
c(.025, .5, .975))

17. Mean Response
Covariate
Set Nesting Size Status
A 4 Small Migrant
B 4 Small Resident
C 4 Large Migrant
D 4 Large Resident

18. Mean Response
cov1 = c(1, 4, 0, 0)
cov2 = c(1, 4, 1, 0)
cov3 = c(1, 4, 0, 1)
cov4 = c(1, 4, 1, 1)
X1 =rbind(cov1,cov2,cov3,cov4)
mean.draw = blinregexpected(X1,
par.sample)

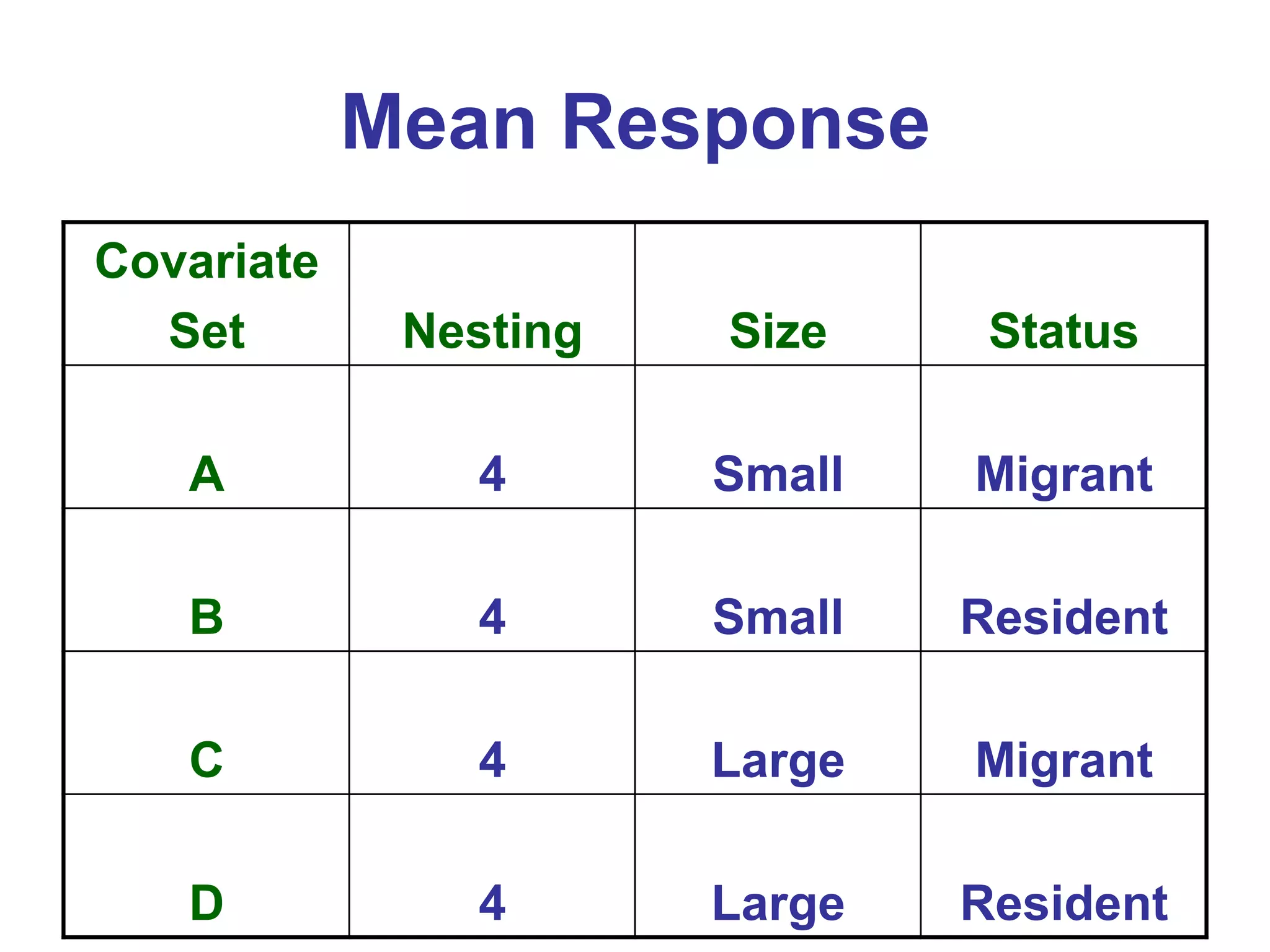
19. Mean Response
op = par(mfrow = c(2,2))
hist(mean.draw[, 1],
main = "Covariate Set A",
xlab = "Log Time")
hist(mean.draw[, 2],
main = "Covariate Set B",
xlab = "Log Time")

20. Mean Response
hist(mean.draw[, 3],
main = "Covariate Set C",
xlab = "Log Time")
hist(mean.draw[, 4],
main="Covariate Set D",
xlab="Log Time")
par(op)

21. Means Response’ Summary
• Compute 2.5th , 50th & 97.5th percentiles
apply(mean.draw, 2, quantile,
c(.025, .5, .975))

22. Future Response
pred.draw=blinregpred(X1, par.sample)
op = par(mfrow = c(2,2))
hist(pred.draw[, 1], main="Covariate
Set A", xlab="Log Time")
hist(pred.draw[, 2], main="Covariate
Set B", xlab="Log Time")

23. Future Response
hist(pred.draw[, 3],
main="Covariate Set C",
xlab="Log Time")
hist(pred.draw[, 2],
main="Covariate Set D",
xlab="Log Time")
par(op)

24. Future Response’ Summary
• Compute 2.5th , 50th & 97.5th percentiles
apply(pred.draw, 2, quantile,
c(.025, .5, .975))